Тема 1. Временные ряды

Временной ряд – ряд наблюдени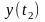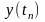й , ,…., или 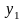, ,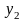…., , 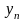который анализирует случайные величины 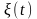, произведенные в последовательные периоды времени , ,…., .

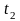Для временных рядов порядок наблюдений является критичным и не допускает….. (посмотри у себя в конспекте, а то у меня пропущено).

Отдельные элементы временного ряда называются уровнем ряда.

Типы временных рядов

По способу формирования:

1. Моментный – такой временной ряд каждый уровень которого формируется за счет показателя наблюдения в определенный момент времени.

2. Интервальный - временной ряд каждый уровень которого является результатом суммирования наблюдаемых значений показателя за определенный период.

По времени фиксирования уровней ряда:

1. Полный дискретный ряд – между уровнями которого одинаковые промежутки времени.

2. Неполный дискретный ряд – такой временной ряд между уровнями которого различные промежутки времени.

По природе данных:

1. Непрерывные

2. Дискретные

Каждый уровень ряда несет в себе случайную и детерминированную компоненту.

Детерминированная компонента – часть уровня ряда изменение которой подчинено некоторой закономерности.

Случайная компонента – отражает отклонение фактического уровня ряда от детерминированной компоненты и обусловлено сложностью наблюдений явлений и процессов.

В анализе временного ряда в качестве универсального объясняющего фактора используется фактор времени.

Использование фактора времени позволяет аккумулировать влияние большого числа факторов влияющих на уровень ряда при условии отсутствия явно доминирующего фактора.

В результате анализа временного ряда решаются следующие задачи:

1. Проверка временного ряда на случайность.

2. Выявление состава неслучайных компонент и построение модели неслучайных компонент.

3. Оценка диапазонов изменений случайной компоненты.

Среди неслучайных компонент временного ряда встречают:

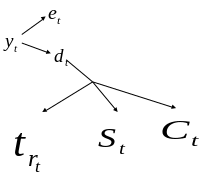
Аддитивная и мультипликативная модель временного ряда:

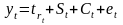- аддитивная

- мультипликативная

Важным допущением регрессионного анализа является нормальное распределение ошибки.

Тема 2. Основные методы тестирования временных рядов

2.1. Проверка временного ряда на случайность

2.1.1.Критерий серий, основанный на медиане выборки

Основные шаги метода:

Шаг 1.По исходному ВР рассчитывается медиана (ряд ранжируется и выбирается значение посередине либо формула =МЕДИАНА())

Шаг 2. Замена исходного ряда рядом из + и – по следующему правилу: если уровень ряда больше медианы – ставим +, если меньше - ставим –. Если уровень равен медиане – ничего не ставим.

Замечание: пропущенные значения + и – разбивают серию, даже если после пропущенного значения идет такой же знак, как и до него.

Для случайного ряда характерны:

• большое количество серий

• малая длина серий

Для неслучайного ряда характерны

• малое кол-во серий

• большая длина серий

Серия считается длинной, если ее длина больше, чем

[1,43 ln (n+1)](целая часть числа)

Количество серий считается большим, если оно больше, чем

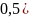[ ] (целая часть числа)

Условие случайности ВР : количество серий большое и длина максимальной серии меньше критического значения.

2.1.2. Критерий восходящих и нисходящих серий

Шаг 1. Каждый уровень ряда, начиная со второго, заменяется на +, если текущий уровень ряда больше предыдущего, и -, если текущий уровень ряда меньше предыдущего.

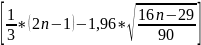-критическое значение для количества серий

n≤26	5
26<n≤153	6
153<n≤1170	7
n>1170	8

критическое значение для длины серии в зависимости от количества уровней ряда

Условие случайности ВР:

• Количество серий больше критического значения для количества серий

• Длина максимальной серии меньше критического значения для длины серии