МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ИЖЕВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ М.Т.КАЛАШНИКОВА»

ФАКУЛЬТЕТ «ИНФОРМАТИКА И ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА»

КАФЕДРА «ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА»

Пояснительная записка к курсовому проекту

по дисциплине «Схемотехника ЭВМ»

На тему «Минимизация и факторизация булевой функции»

Вариант № 12-12.

Выполнил: студент 3 курса

группы Б06-781-1зт

Хабибуллина Л.М.

_______________________

Проверил:

д. т. н. профессор

Гитлин В.Б.

_______________________

Ижевск

2014 год.

СОДЕРЖАНИЕ

С.

	Цель работы………………………………………………………………	3
1.	Исходные данные………………………………………………………..	3
2.	Построение карт Карно………………………………………………….	3
3.	Переход от булевых выражений к функциональным схемам………..	5
4.	Минимизация заданной функции………………………………………	7
5.	Факторизация покрытий………………………………………………...	9
6.	Схемная реализация факторизированного покрытия…………………	13
7.	Перевод схемы в универсальный базис………………………………..	14
8.	Описание работы схемы………………………………………………...	18
	ЗАКЛЮЧЕНИЕ………………………………………………………….	20
	СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ……………………	21

Цель работы: преобразовать данную булеву функцию, минимизировать ее произвести факторизацию, оценить экономию, а также выполнить схемную реализацию факторизованного покрытия

1. Исходные данные

Вариант № 12

Тип множества	12
L	011X0 0011X 101X1 00X0X 111XX 0X010 01011

Схема №12

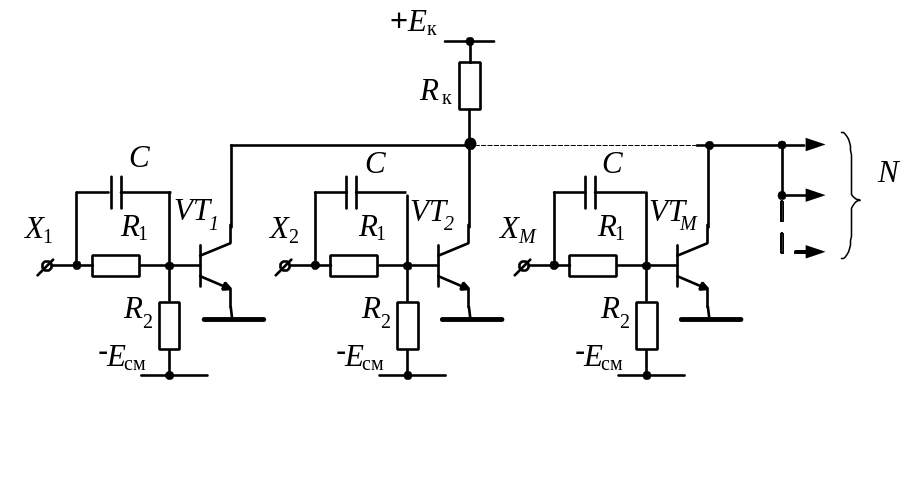
2. Построение карт Карно

Для проведения минимизации составим карты Карно для пяти переменных по следующей схеме

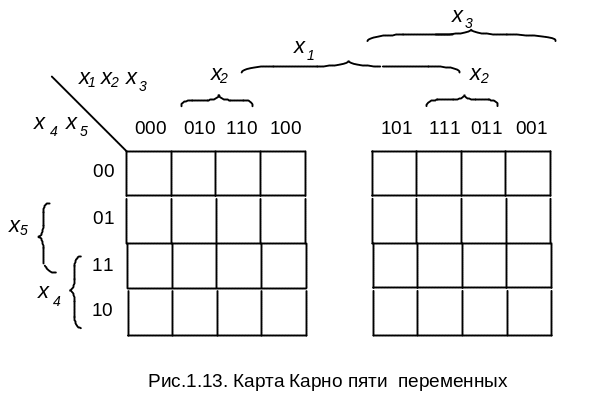
Рисунок 1 – Карта Карно пяти переменных

Данный набор содержит в себе кубы различно размерности: одномерной, двухмерной и нулевой.

Одномерный куб e12. На этом кубе переменная x1 может принимать значения 0 и I. Для каждого значения x1 функция f(x1) также может принимать значения либо 0, либо 1.

. Двумерный куб ^* На этом кубе переменные я ж^ могут принимать одно из значений 0 ила I; всего воз­можно четыре комбинации,- что отпечено на рис.3 кружками. На первой позиции каждой ком­бинации отмечено значение х₍ , на второй -позиции - зс^ , Для каждой из комбинаций я,: одно аз значений; 0 или I.

3.

Двумерный куб E₂². На этом кубе переменные x₁ и x₂ могут принимать одно из значений: 0 или 1. Для каждой из комбинаций x₁x₂ функция F(x₁x₂) может принимать одно из значений: 0 или 1.

В исходных данных задана функция F(x₁, x₂, x_3, х₄, х₅), которая равна 1 на следующих наборах

Дизъюнктивная нормальная форма такой функции

.

Построим для данной функции карты Карно

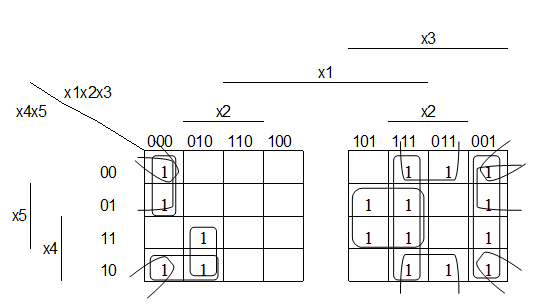
Рисунок 2 – Карта Карно для исходных данных

Построение карт Карно по данным функциям производилось следующим образом, на примере набора 011X0. Так как вторая и пятая координата куба равны 0, а вторая и третья равны 1, то единицы проставляем во всех клетках, где вторая и пятая координата куба равны 0, а вторая и третья равны 1. Четвертая позиция может быть как равна 0 так и 1, что проставляем единицы в клетках, где четвертая позиция равна 0, либо 1. Аналогично заполняются клетки для оставшихся кубов

3. Переход от булевых выражений к функциональным схемам

При переходе от кубической записи булевой функции к функци­ональной схеме переменные одного куба объединяются знаком конъюнк­ции, т.е. являются входами одной схемы И, все кубы объединяются друг с другом знаком дизъюнкции, т.е. выходы схем И являются входами одной схемы ИЛИ. Около входа схемы И ставится переменная без инверсии, если на соответствующем месте в кубе стоит 1; с инверсией, если на соответствующем месте в кубе стоит нуль; вход остается пустым, если на соот­ветствующей месте стоит X.

Строим функциональную схему для исходных данных.

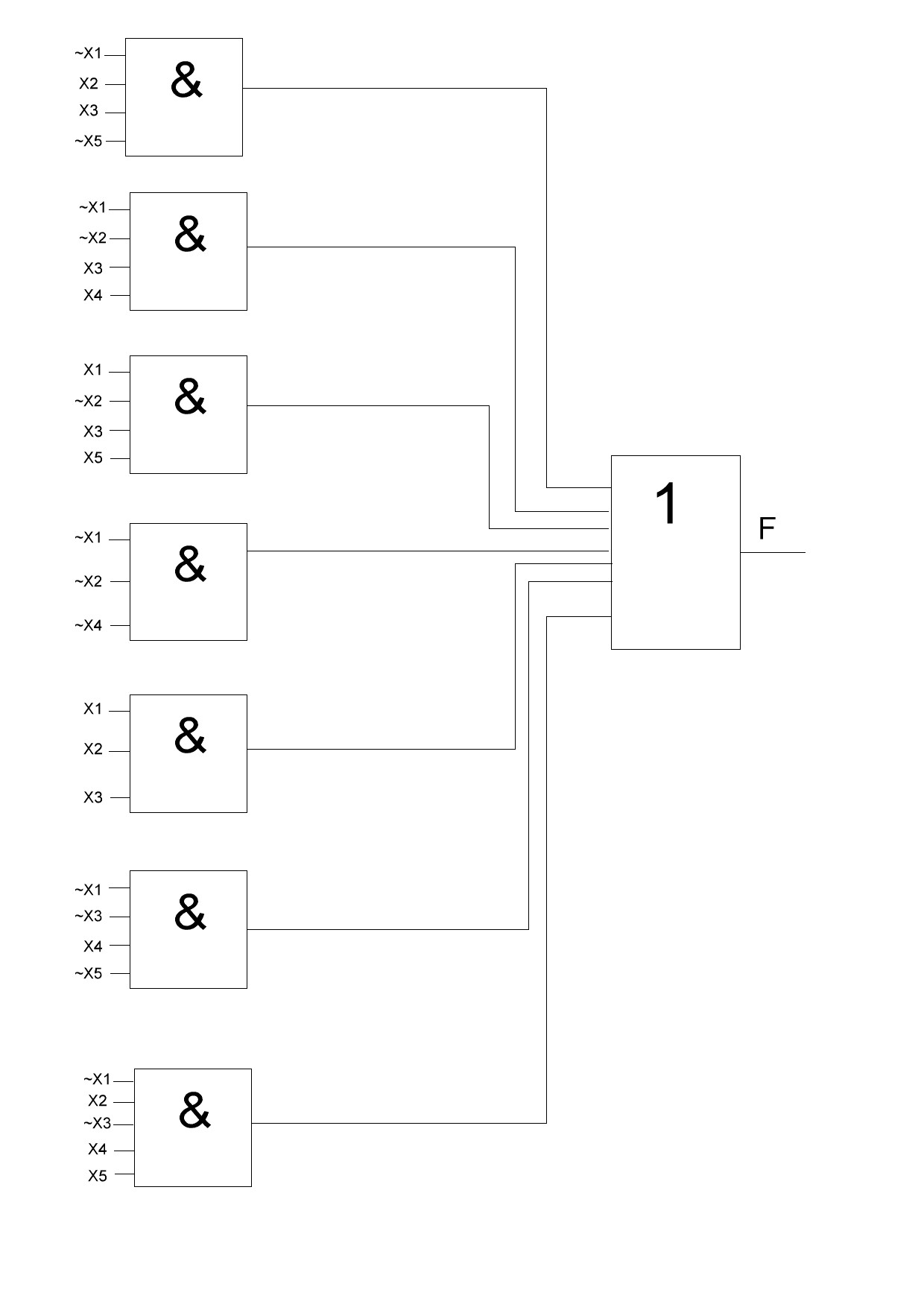
Рисунок 3 – функциональная схема

Найдем стоимость схемы по следующей формуле:

, (1)

Где n - общее число координат,

r – размерность куба

К - число кубов, на которых функция равна 1

4. Минимизация заданной функции

Используются следующие принципы минимизации:

1. Построить максимальные кубы на клетках, где функций 1 (простые импликанты).

2. Найти клетки, которые покрываются только одним кубом (обособленные клетки или вершины куба).

3. Включить в минимальное покрытие все кубы, которые покрывают обособленные клетки.

4. Удалить из рассмотрения покрытые клетки. Выбросить из рассмотрения кубы, которые покрывали что-то из выбранных клеток, если клетки, покрываемые отбрасываемыми кубами, имеют другое покрытие в виде другого куба равной или большей размерности по сравнению с отбрасываемым кубом.

5. Продолжить процесс поиска.

Таким образом следуя данному принципу минимизации отброшенными из рассмотрения кубами будут: 00Х0Х, 00ХХ0. 111ХХ.

Кубами вошедшими в минимальное покрытие станут:

1X1X1, 001XX, X11X0, 0101X, 0000X, 0X010

Окончательное минимальное покрытие будет выглядеть следующим образом:

Функциональная схема после минимизации

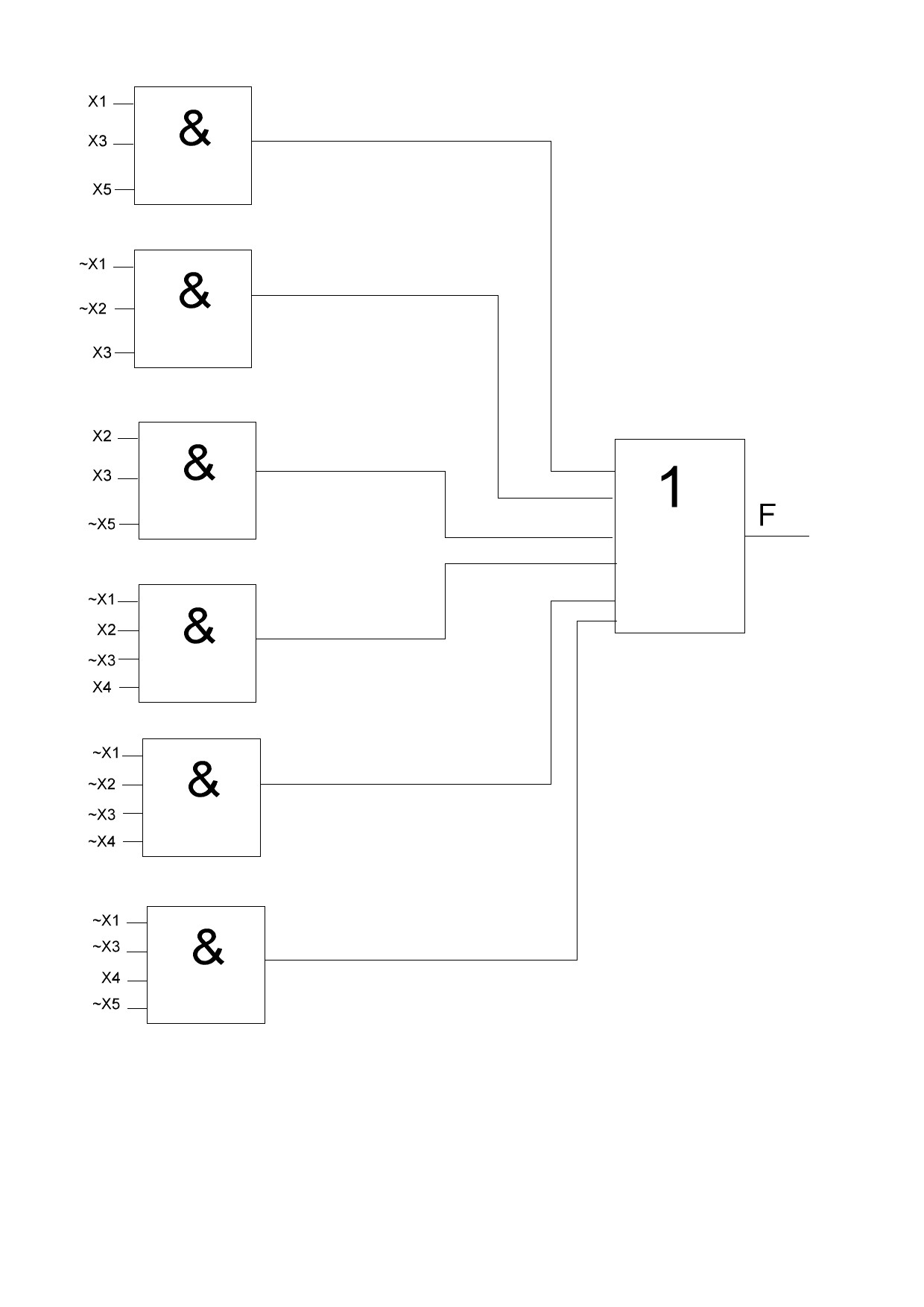
Рисунок 4 – Функциональная схема после минимизации функции

Рассчитаем стоимость:

Рассчитаем экономию:

Стоимость схемы до минимизации

W(C(F))=34

Стоимость после минимизации

W(C(F))_min=25

Выигрыш в стоимости составляет

ΔW=34-25=9