
- •9.Спиновые квантовые числа и спиновые моменты электрона. Опыты Штерна и Герлаха.
- •11. Главное квантовое число n – число, которое определяет энергетические уровни электрона в атоме и может принимать любые целые значения.
- •19. Распределение Ферми-Дирака:
- •23. Зависимость электрического сопротивления металлов от температуры
- •Вопрос 27
- •Вопрос 28
- •Вопрос 29
- •Вопрос 31.
- •Вопрос 32.
1.корпускулярно-волновой дуализм— принцип, согласно которому любой объект может проявлять как волновые, так и корпускулярные свойства.Корпускулярные свойства света проявляются при фотоэффекте и в эффекте Комптона. Фотон ведет себя и как частица, которая излучается или поглощается целиком объектами, размеры которых много меньше его длины волны (например, атомными ядрами), или вообще могут считаться точечными (например, электрон).
Волны
де бройля —
волны, связанные с любыми микрочастицами и
отражающие их волновую природу.![]() и
длина волны
и
длина волны ![]() ,
где
,
где ![]() — постоянная
Планка,р-импульс.
— постоянная
Планка,р-импульс.
2.
принцип необпред гейзенберга в квантовой
механике — фундаментальное
неравенство (соотношение неопределённостей),
устанавливающее предел точности
одновременного определения пары
характеризующих систему квантовых наблюдаемых,
описываемых некоммутирующими операторами (например,координаты и
импульса, тока и напряжения, электрического
и магнитного поля).Согласно принципу
неопределённостей у частицы не могут
быть одновременно точно измерены
положение и скорость (импульс). Принцип
неопределённости уже в виде, первоначально
предложенном Гейзенбергом, применим
и в случае, когда не реализуется ни одна
из двух крайних ситуаций. Соотношение
неопределенностей — строгий закон
природы, который никак не связан с
несовершенством наших приборов. Оно
утверждает: нельзя — принципиально
нельзя — определить одновременно
и координату и импульс частицы точнее,
чем это допускает приведенное неравенство.
![]()
![]()
3.Микрообъекты - к микрообъектам относятся молекулы, атомные ядра, элементарные частицы. Спин микрообъекта. Одной из важнейших специфических характеристикмикрообъекта является спин. Спин можно интерпретировать как
своеобразный момент импульса микрообъекта, не связанный с движениеммикрообъекта как целого, неуничтожимый, не зависящий от внешних условий (егочасто называют внутренним моментом импульса микрообъекта) . Квадрат этогомомента импульса равен h2s(s+1) . Здесь s – определенное для данногомикрообъекта целое или полуцелое положительное число (именно это число иназывают обычно спином) , h – универсальная физическая постоянная, играющая вквантовой механике исключительно важную роль. Ее называют постояннойПланка; Нестабильность микрообъектов. Все элементарные частицы, заисключением фотона, электрона, протона и обоих нейтрино, нестабильны.Это означает, что они самопроизвольно, без каких-либо внешних воздействий
распадаются, превращаясь в другие частицы волновому закону меняется не сама вероятность, а величина, названная амплитудой вероятности и обозначенная фи(x,y,z,t)Эту величину называют волновой функцией.Св-ва: функция фи должна быть конечной(вероятность не может быть>1),однозначной и непрерывной .
4.Движение
электрона в области одномерной
потенциальной ямы.
Изменение
потенциальной энергии по оси x описывается
формулой -![]() Всю
область изменения переменной x разобьем
на три. Вероятность нахождения частицы
в областях x < 0 и x > a равна
нулю, так что волновая функция Ψ(x) =
0. В центральной части мы положили для
удобства U(x) = 0. В этом случае уравнение
Шредингера принимает вид
Всю
область изменения переменной x разобьем
на три. Вероятность нахождения частицы
в областях x < 0 и x > a равна
нулю, так что волновая функция Ψ(x) =
0. В центральной части мы положили для
удобства U(x) = 0. В этом случае уравнение
Шредингера принимает вид
![]()
где m и E –
масса и полная энергия частицы,
соответственно. Введем обозначение
![]() Уравнение приобретает вид и имеет
решение
Уравнение приобретает вид и имеет
решение
![]() Постоянные A, α и β мы
найдем из условий непрерывности волновой
функции и нормировки. На левой
границе Ψ(0) = Asin(α) = 0 дает α =
0. На правой границе Ψ(a) = Asin(βa)
= 0 приводит к βa = πn, где n =
1, 2, 3, ... Движение частицы в потенциальной
яме описывается набором волновых
функций
Постоянные A, α и β мы
найдем из условий непрерывности волновой
функции и нормировки. На левой
границе Ψ(0) = Asin(α) = 0 дает α =
0. На правой границе Ψ(a) = Asin(βa)
= 0 приводит к βa = πn, где n =
1, 2, 3, ... Движение частицы в потенциальной
яме описывается набором волновых
функций
![]() Условие
нормировки
Условие
нормировки
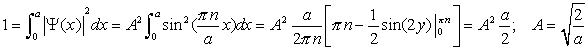 Окончательный
вид волновой функции
Окончательный
вид волновой функции
![]() Возведем
в квадрат левую и правую части
равенства βa = πn, и вспомним,
что значит β2. Тогда получим выражение
для энергии
Возведем
в квадрат левую и правую части
равенства βa = πn, и вспомним,
что значит β2. Тогда получим выражение
для энергии
![]() Самым важным результатом
является то, что возможны только такие
состояния, для которых E принимает
одно из дискретных значений. Введенное
выше число n называют квантовым
числом. Значения En называют уровнями
энергии. Состояние с минимальной
энергией (n = 1) называют основным,
остальные - возбужденными.
Самым важным результатом
является то, что возможны только такие
состояния, для которых E принимает
одно из дискретных значений. Введенное
выше число n называют квантовым
числом. Значения En называют уровнями
энергии. Состояние с минимальной
энергией (n = 1) называют основным,
остальные - возбужденными.
Распределение плотности вероятности по координате |Ψ(x)|2 неоднородно и зависит от n. Чем больше n, тем сильнее неоднородность. С классической точки зрения на частицу в яме не действуют никакие силы, и она с равной вероятностью может находиться в любой точке.
Расстояние между соседними уровнями энергии
![]()
Найдем еще относительное расстояние между уровнями
![]() Фактически
наблюдаем переход к непрерывному
изменению энергии.
Фактически
наблюдаем переход к непрерывному
изменению энергии.
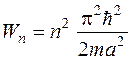 энергия
частицы в пот яме принимает лишь
определен дискрет значение,т.е
квантуется,квантованное значение назыв
уровнями энергии
энергия
частицы в пот яме принимает лишь
определен дискрет значение,т.е
квантуется,квантованное значение назыв
уровнями энергии
5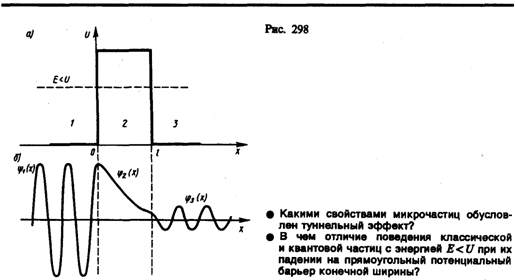
 .Прохождение
микрообъекта через потенциальный
барер.Туннельный эффект.
Туннельный
эффект – явление в рез которого
микрообъект может пройти сквозь потенц
барьер
Прохождение микрообъекта
через потенциальный барер -
.Прохождение
микрообъекта через потенциальный
барер.Туннельный эффект.
Туннельный
эффект – явление в рез которого
микрообъект может пройти сквозь потенц
барьер
Прохождение микрообъекта
через потенциальный барер -
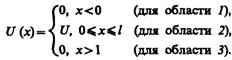 При
данных условиях задачи классическая
частица, обладая энергией Е, либо
беспрепятственно пройдет над барьером
(при Е>U), либо
отразится от него (приЕ<U) и
будет двигаться в обратную сторону, т.
е. она не может проникнуть сквозь барьер.
Для микрочастицы же, даже при Е>U, имеется
отличная от нуля вероятность, что
частица отразится от барьера и будет
двигаться в обратную сторону.
При E<U имеется
также отличная от нуля вероятность,
что частица окажется в области х>1, т.
е. проникает сквозь барьер.
Уравнение
Шредингера для стационарных состояний
для каждой из выделенных областей
имеет вид
6.
Уравнение Шредингера основное уравнение
нерелятивистской квантовой
механики
уравнение
шредингера — уравнение, описывающее
изменение в пространстве (в общем
случае, в конфигурационном
пространстве)
и во времени чистого
состояния,
задаваемого волновой
функцией,
в гамильтоновых квантовых
системах. Играет в квантовой
механике такую
же важную роль, как уравнение второго
закона Ньютона в классической
механике.
При
данных условиях задачи классическая
частица, обладая энергией Е, либо
беспрепятственно пройдет над барьером
(при Е>U), либо
отразится от него (приЕ<U) и
будет двигаться в обратную сторону, т.
е. она не может проникнуть сквозь барьер.
Для микрочастицы же, даже при Е>U, имеется
отличная от нуля вероятность, что
частица отразится от барьера и будет
двигаться в обратную сторону.
При E<U имеется
также отличная от нуля вероятность,
что частица окажется в области х>1, т.
е. проникает сквозь барьер.
Уравнение
Шредингера для стационарных состояний
для каждой из выделенных областей
имеет вид
6.
Уравнение Шредингера основное уравнение
нерелятивистской квантовой
механики
уравнение
шредингера — уравнение, описывающее
изменение в пространстве (в общем
случае, в конфигурационном
пространстве)
и во времени чистого
состояния,
задаваемого волновой
функцией,
в гамильтоновых квантовых
системах. Играет в квантовой
механике такую
же важную роль, как уравнение второго
закона Ньютона в классической
механике. 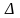 оператор
лапласа,hпостоянн лирака,Uпотенц энергия
частицы в силовом поле,в кот она
движется
оператор
лапласа,hпостоянн лирака,Uпотенц энергия
частицы в силовом поле,в кот она
движется
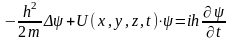
7.Стационарное уравнение Шредингера для электрона ВДПА. Главное квантовое число.
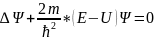 -уравнение
для стационарных состояний.
-уравнение
для стационарных состояний.
Атом водорода и водородоподобной системы – это система, состоящая из ядра с зарядом Ze и одного электрона.Главное квантовое число n – число, которое определяет энергетические уровни электрона в атоме и может принимать любые целые значения.
8.Орбитальное
квантовое число и орбитальные моменты
электрона. Магнитное орбитальное
квантовое число.Орбитальное
квантовое число l – число, которое при
заданном n принимает значения 0,1…(n-1),
т.е. всего n-значений и определяет момент
импульса электрона в атоме. Орбитальный
магнитный момент электрона:
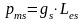
Орбитальный
механический момент электрона
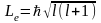
Магнитное
квантовое число
 определяет проекцию момента импульса
электрона на заданное направление,
причём вектор момента импульса электрона
в атоме может иметь в пространстве
(2l+1) ориентаций.
определяет проекцию момента импульса
электрона на заданное направление,
причём вектор момента импульса электрона
в атоме может иметь в пространстве
(2l+1) ориентаций.
9.Спиновые квантовые числа и спиновые моменты электрона. Опыты Штерна и Герлаха.
Электрон
обладает собственным неуничтожимым
механическим моментом импульса - спином.
Спин электрона и др. микрочастиц -
квантовая величина. Если электронам
приписывается собственный механический
момент импульса – спин
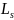 ,
то ему соответствует собственный
магнитный момент
,
то ему соответствует собственный
магнитный момент
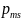 .
Спин квантуется по закону
.
Спин квантуется по закону
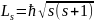
s-спиновое квантовое число.
Вектор
прнимает (2s+1) ориентацию, т.к. в опытах
Штерна и Герлаха наблюдаются только 2
ориентации, то 2s+1=2, s=1/2.,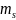 -магнитное
спиновое квантовое число
-магнитное
спиновое квантовое число
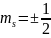 Магнитное спиновое квантовое число
-
число, которое определяет проекцию
спина на направление внешнего магнитного
поля.Целью опытов Штерна и Герлаха
являлось изменение магнитных моментов
атомов различных элементов. Идея опытов
заключалась в измерении силы действующей
на атом в неоднородном м.п. Опыты
обнаружили ошибочность предположения
о том, что магнитный момент
Магнитное спиновое квантовое число
-
число, которое определяет проекцию
спина на направление внешнего магнитного
поля.Целью опытов Штерна и Герлаха
являлось изменение магнитных моментов
атомов различных элементов. Идея опытов
заключалась в измерении силы действующей
на атом в неоднородном м.п. Опыты
обнаружили ошибочность предположения
о том, что магнитный момент
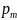 и механический момент импульса L атома
произвольно ориентирован относительно
напр. внешнего поля и подтвердили
наличие пространственного
квантования.Проводя прямые измерения
магнитных моментов Ш. и Г. обнаружили,
что узкий пучок атомов водорода,
находящийся в состоянии S в неоднородном
м.п. расщепляется на 2 пучка. В этом
состоянии момент импульса = 0, и м.п. не
должно оказывать влияние на движ. атомов
водорода в основном состоянии, т.е
расщепления быть не должно. В дальнейшем
было доказано, что спектральные лини
атома водорода обнаруж. тонкую
структуру(явл. дубликатами) даже в
отсутсвии м.п.
и механический момент импульса L атома
произвольно ориентирован относительно
напр. внешнего поля и подтвердили
наличие пространственного
квантования.Проводя прямые измерения
магнитных моментов Ш. и Г. обнаружили,
что узкий пучок атомов водорода,
находящийся в состоянии S в неоднородном
м.п. расщепляется на 2 пучка. В этом
состоянии момент импульса = 0, и м.п. не
должно оказывать влияние на движ. атомов
водорода в основном состоянии, т.е
расщепления быть не должно. В дальнейшем
было доказано, что спектральные лини
атома водорода обнаруж. тонкую
структуру(явл. дубликатами) даже в
отсутсвии м.п.
10.
Главное квантовое число n
– число, которое определяет энергетические
уровни электрона в атоме и может
принимать любые целые значения.. Атом
Н и ВДПА – система состоящая из ядра
с зарядом ze и одного е. Энергия электрона
в атоме водорода:
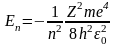
Z-поряд ном элем,зарядовое число,Амассовое число
11. Главное квантовое число n – число, которое определяет энергетические уровни электрона в атоме и может принимать любые целые значения.
Орбитальное квантовое число l – число, которое при заданном n принимает значения 0,1…(n-1), т.е. всего n-значений и определяет момент импульса электрона в атоме.
Магнитное квантовое число определяет проекцию момента импульса электрона на заданное направление, причём вектор момента импульса электрона в атоме может иметь в пространстве (2l+1) ориентаций.
Магнитное спиновое квантовое число - число, которое определяет проекцию спина на направление внешнего магнитного поля.
Орбитальный магнитный момент электрона: g-гиромаг отнош спиновых мом,Les-спинОрбитальный механический момент электрона l-орбит квант чис
12. Принцип Паули: обобщая общие данные Паули сформировал принцип, согласно которому система фермионов (частиц с полуцелым спином) встречается в природе только в состояниях, описываемых антисимметричными волновыми функциями. Принцип Паули помогает объяснить разнообразные физические явления. Следствием принципа является наличиеэлектронных оболочек в структуре атома, из чего, в свою очередь, следует разнообразие химических элементов и их соединений. Количество электронов в отдельном атоме равно количеству протонов. Распред эл по различ квант сост подчин принципу паули соглнасно кот в одном состоянии не может быть 2-х одинак эл(с одинак набором 4-х квантовых чисел)они должны отлич,например напревлением спина
13) Электронная оболочка – совокупность электронов в многоэлектронном атоме имеющих одно и то же главное квантовое число n.В каждой из оболочек электрона распределяются на подоболочки соответствующим данномуl. В многоэлектронных атомах на каждый электрон действует не только ядро, но и все остальные электроны. При этом электронные облака отдельных электронов как бы сливаются в одно общее многоэлектронное облако. Электроны в атоме расположены на энергетических уровнях, которые со- держат различные энергетические подуровни, состоящие, в свою очередь, из определенного количества атомных орбиталей: s- подуровень состоит из одной, р- подуровень ─ из трех, d- подуровень ─ из пяти и f- подуровень ─ из семи орбиталей.
14) Спектр – набор частот или длины волны излучения которое излучает тело. Линейчатый спектр – совокупность отдельных линий, появляющихся на фоне сплошного спектра.
Сплошной - это спектр, содержащий все длины волн определенного диапазона от красного с λ ≈ 7,6.10-7 м до фиолетового с λ ≈ 4.10-7 м. Сплошной спектр излучают нагретые твердые и жидкие вещества, газы, нагретые под большим давлением.Тормозной спектр – это сплошной рентгеновский спектр.
Обобщённая
формула Бальмера:
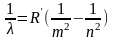
Больмер подобрал формулу описывающую все известные линии атома водорода в видимой области спектра. ТЕРМЫ СПЕКТРАЛЬНЫЕ -уровни энергии атома, иона или молекулы, характеризующиеся определ. значениями полного орбитального момента L и полного спина S электронов.Rштрих постоянная гидберга,R=Rштрх*с
15.16) Спонтанное излучение – процесс испускания фотона возбуждённым атомом без каких-либо внешних воздействий.Вынужденное излучение — излучение атомов фотона дополнительно к тому фотону, под действием которого произошёл переход.Структура энергетических уровней молекул определят их спектр излучения, возникающий при квантовых переходах между соответствующими энергетическими уровнями. Электроны в атоме расположены на энергетических уровнях, которые со- держат различные энергетические подуровни, состоящие, в свою очередь, из определенного количества атомных орбиталей: s- подуровень состоит из одной, р- подуровень ─ из трех, d- подуровень ─ из пяти и f- подуровень ─ из семи орбиталей. При распределении электронов по квантовым ячейкам следует руководство- ваться принципом Паули: в атоме не может быть двух электронов с одинаковым набором значений всех квантовых чисел, т. е. атомная орбиталь не может содер- жать более двух электронов, причем их спиновые моменты должны быть проти-воположными. Состояние с инверсией населенностей – неравномерное состояние системы, при котором число атомов в возбуждённых состояниях было больше, чем их число в искомом состоянии
18.
Периодический закон был сформулирован
Д. И. Менделеевым в следующем
виде (1871): «свойства простых тел, а также
формы и свойства соединений элементов,
а потому и свойства образуемых ими
простых и сложных тел, стоят в периодической
зависимости от их атомного веса».
Заполнение электронами состояний в
атомах происходит в порядке возрастания
их энергий и понижения полной энергии
атомов. При этом выполняется принцип
Паули, и каждое состояние может быть
занято либо одним, либо двумя электронами.
В последнем случае электроны обязательно
имеют противоположные спины и называются
спаренными Для нейтральных атомов в
основном состоянии последовательность
заполнения АО следующая:
![]()
