1.Предмет и основные задачи геодезии

Геодезия—наука о производстве измерений на местности, определении фигуры и размеров Земли и изображении земной поверхности в виде планов и карт.

Задачи геодезии:

1) НАУЧНАЯ(основная):определение формы и размеров Земли как планеты в целом.

Современные научные задачи:

• исследование динамики земной коры;

• определение разностей уровней морей;

• определение движения полюсов Земли;

- изучение внешнего гравитационного поля Земли и др.

2) НАУЧНО-ТЕХНИЧЕСКИЕ:

• распространение единой системы координат на обширные территории;

• создание геодезических сетей;

• создание и внедрение ГИС - геоинформационных систем;

• разработка способов, приемов и средств геодезических измерений на земной поверхности.

3) ПРИКЛАДНЫЕ ЗАДАЧИ:

• составление топографических карт и планов участков местности;

• геодезическое обеспечение строительства (проектирование, строительство и эксплуатация сооружений);

- создание государственных и локальных кадастров: земельного, водного, лесного, городского и т.д.

2.Системы координат применяемые в геодезии

Системы координат можно классифицировать по ряду признаков. Приведем некоторые из них.

1. По расположению начал. Если начало отсчета совпадает с центром масс Земли, то такая система называется геоцентрической. При расположении начала отсчета на поверхности Земли получим топоцентрическую систему.

2. По виду координатных линий.

Прямоугольные: x, y, z - в пространстве, x, y - на плоскости; криволинейные: сферические , , Н - на шаре, эллипсоидальные B, L, H - на эллипсоиде, последние часто называют просто геодезическими.

3. По назначению. Для описания положения небесных объектов используются звездные системы. Для объектов, участвующих в суточном вращении Земли, используются земные системы координат.

3.Понятие о форме и размерах Земли

Фигуру Землю в первом приближении можно считать шаром со средним радиусом 6371,3 км. В действительности Земля не является идеальной сферой. Из-за суточного вращения она сплюснута с полюсов; высоты материков различны; приливные деформации также искажают форму поверхности. В геодезии для описания фигуры Земли выбирают эллипсоид вращения или геоид.

Поверхность Земли S = 510 000 000 км.кв.

Из них 71% - океан, 29% - суша.

Средняя высота Земли H средняя = 875 м.

Средняя глубина океана D средняя= 3800 м

4 Что такое карта, план, профиль. Понятие о проекциях.

Топографическая карта — уменьшенное изображение на плоскости значительных участков земной поверхности, построенное в определенной картографической проекции, с учетом кривизны Земли.

План (топографический) — уменьшенное изображение проекций небольших участков земной поверхности на горизонтальную плоскость.

Планы составляются обычно в крупных масштабах, местность на них характеризуется, как правило, более детально, чем на картах.

Профилем местности называется уменьшенное изображение вертикального разреза земной поверхности по заданному направлению.

5.Разграфка и номенклатура карт

Разграфка карт — система деления карт на отдельные листы.

Система обозначения листов многолистной карты называется номенклатурой. В основу номенклатуру положено международная разграфка листов карты масштаба 1:100000. Листы карты этого масштаба ограничены меридианами и параллелями по широте 4 градуса, по долготе 6. Такой лист обозначается заглавной латинской буквой, определяющей горизонтальный полюс, и арабской буквой, определяющей номер вертикальной колонки. Разграфка карт масштаба крупнее 100000 получается последовательным делением листа карты масштаба 1:100000. Одному листу карты масштаба 1:100000 соответствует: 4 листа карты масштаба 1:500000, обозначаемые буквами АБВГ, 9 листов масштаба 1:300000 обозначаемыми римскими цифрами I..IX, 36 листов масштаба 1: 200000 обозначаемыми также римскими цифрами, 144 листа масштаба 1:100000 обозначаемыми цифрами от 1-144.

6. Масштаб, виды масштабов, точность масштаба.

Степень уменьшения горизонтальных проекций линий местности при изображении их на плане или карте называется масштабом.

Масштаб – это отношение длины отрезка s на плане или карте к горизонтальной проекции соответствующего отрезка S на местности.

Линейный масштаб представляет собой шкалу с делениями, соответствующими данному числовому масштабу. Для построения линейного масштаба на прямой линии откладывают несколько раз расстояние, называемое основанием масштаба

Поперечный масштаб применяют для измерений и построений повышенной точности. Как правило, поперечный масштаб гравируют на металлических пластинах, линейках или транспортирах.

Масштаб бывает численный (1:5000), именованный («в 1 см 50 м») и графический (линейный и поперечный).

Численный масштаб представляет собой правильную дробь, у которой числитель равен 1, а знаменатель указывает, во сколько раз уменьшена длина линии местности при ее изображении на карте:

где М – знаменатель численного масштаба. Чем больше знаменатель численного масштаба, тем больше степень уменьшения горизонтальных проекций линий местности, тем мельче масштаб плана или карты.

Масштабы выбирают кратными десяткам, сотням и тысячам чисел 1; 2; 5; 25, такие, как 1:5 000, 1:25 000, 1:200 000. Не выбирают масштабы типа 1:7000 или 1:33 000. Если знаменатель численного масштаба разделить на 100 (зачеркнуть два последних нуля), то получится число, которое укажет, сколько метров местности содержится в одном сантиметре карты.

Горизонтальное расстояние на местности, соответствующее 0,1мм (0,01см) на плане, называется предельной точностью масштаба t_пр, т.е.

,

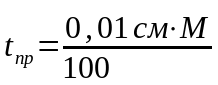Длина отрезка на плане или карте может быть оценена с точностью ±0,2мм. Горизонтальное расстояние на местности, соответствующее в данном масштабе 0,2мм (0,02см) на плане, называется графической точностью масштаба t_граф., т.е.

7.Основные формы рельефа. Способы отображения рельефа на планах и картах.

Гора (холм) - это возвышенность конусообразной формы. Она имеет характерную точку – вершину, боковые скаты (или склоны) и характерную линию – линию подошвы. Линия подошвы – это линия слияния боковых скатов с окружающей местностью. На скатах горы иногда бывают горизонтальные площадки – называемые уступами.

Котловина – это углубление конусообразной формы. Котловина имеет характерную точку – дно, боковые скаты (или склоны) и характерную линию бровки. Линия бровки - это линия слияния боковых скатов с окружающей местностью.

Хребет – это вытянутая и постепенно понижающаяся в одном направлении возвышенность. Он имеет характерные линии: - линию водораздела образуемую боковыми скатами при их слиянии вверху и две линии подошвы.

Лощина – это вытянутое и открытое с одного конца постепенно понижающееся углубление. Лощина имеет характерные линии: одну линию водослива образуемую боковыми скатами при их слиянии внизу и две линии бровки.

Овраг – резко выраженное углубление на равнине, растянутое в одном направлении, с крутыми склонами и временно действующими водостоками. Овраги часто имеют ответвления.

Седловина – это небольшое понижение между двумя соседними горами; как правило седловина является началом двух лощин понижающихся в противоположных направлениях. Седловина имеет одну характерную точку – точку седловины располагающуюся в самом низком месте.

Формы рельефа образуются из сочетания наклонных поверхностей, скатов: ровный скат, выпуклый скат, вогнутый скат, смешанный скат.

Неровности земной поверхности образованные естественным путем называются рельефом. Он изображается на планах и картах следующими методами: метод анимации, метод отмывки (цветная пластика), метод горизонталей.

8.Метод горизонталей. Высота сечения рельефа.

Горизонталь – плавная кривая линия на карте, соединяющая точки с одинаковыми высотными отметками.

Расстояние h между соседними секущими плоскостями называется высотой сечения рельефа, которая устанавливается в зависимости от характера рельефа местности и масштаба съёмки.

9. Ориентирование линий на местности. Азимуты и румбы. Сближение меридианов, склонение магнитной стрелки.

Ориентировать линию - это значит найти её направление относительно другого направления, принятого за исходное.

Угол между исходным направлением и данной линией называется ориентирным. В геодезии за исходное направление принимается истинный, магнитный и осевой меридиан (ось абсцисс) или линия, ему параллельная.

Угол, отсчитываемый от северного направления истинного меридиана по ходу часовой стрелки до данного направления называется истинным азимутом А

Румбом называется острый угол, отсчитываемый от ближайшего направления (северного или южного) исходного меридиана до данного направления.

Угол между направлением меридианов в данных двух точках одной и той же линии называется сближением меридианов γ.

 Магнитный меридиан, как правило, не совпадает с направлением истинного меридиана в данной точке, а образует с ним некоторый угол, называемый склонением магнитной стрелки δ.

10.Дирекционные углы. Прямое и обратное дирекционное направление.

Передача дирекционного угла на сторону при правых и левых измеренных углах.

Угол, отсчитываемый от северного направления осевого меридиана или линии параллельной ему по ходу часовой стрелки до данного направления называется дирекционным углом α. Измеряется от 0° до 360°.

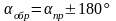
Передача дирекционного угла на сторону теодолитного хода

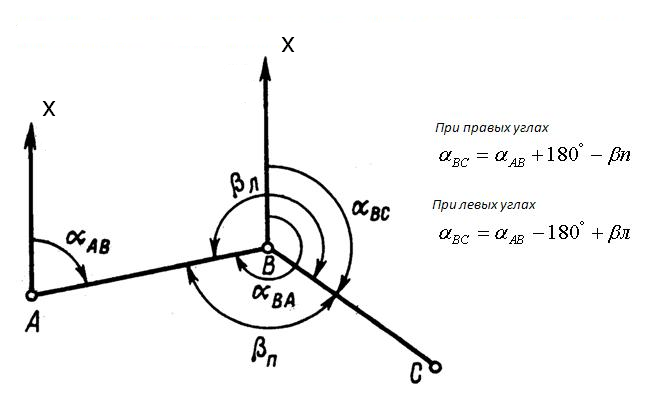
11.Формулы связи ориентирных углов: азимутов, румбов, дирекционных углов.

связь между ориентирными углами:

А=А_м +(±δ), α=А - (±γ);

α= А_м +(±δ)-(±γ).

12. Прямоугольная зональная система координат в проекции Гаусса – Крюгера.

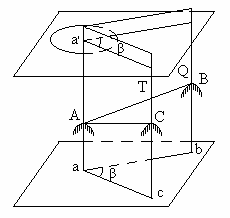
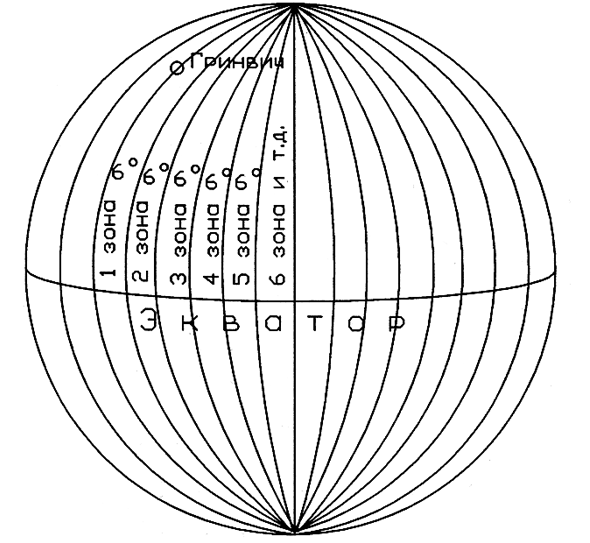
Для изображения земной поверхности К. Гаусс в 1820 г. предложил теорию плоских конформных координат, с помощью которых земной эллипсоид без больших искажений изображается на плоскости. Идея К.Гаусса была реализована Л.Крюгером в систему координат, хорошо удовлетворяющую требованиям практики. Сущность системы координат Гаусса – Крюгера заключается в том, что поверхность земного эллипсоида меридианами, проведенными через 6^О, делится на 60 зон. К центральному (осевому) меридиану каждой зоны проводится перпендикулярно по отношению к оси вращения Земли касательный цилиндр так (Рис.1), чтобы его ось лежала в плоскости экватора.

13.Как по карте определяются: отметки, координаты

При определении координат точек местности по карте применяют географические, плоские прямоугольные и полярные координаты.

ГЕОГРАФИЧЕСКИЕ КООРДИНАТЫ, широта и долгота, определяют положение точки на земной поверхности

Систему плоских прямоугольных координат образуют две взаимно перпендикулярные прямые линии, называемые осями координат; точка их пересечения называется началом или нулем системы координат. Ось абсцисс - OX, ось ординат – OY, делящие плоскость на четверти. Направлениям осей от начала координат приписываются знаки «+» и «-».

Полярные координаты точки на плоскости называются плоскими полярными координатами. Систему полярных координат образует направленный прямой луч OX. Начало координат - точка O - называется полюсом системы, линия OX - полярной осью.

14.Как по карте определяется крутизна ската. Графики заложений

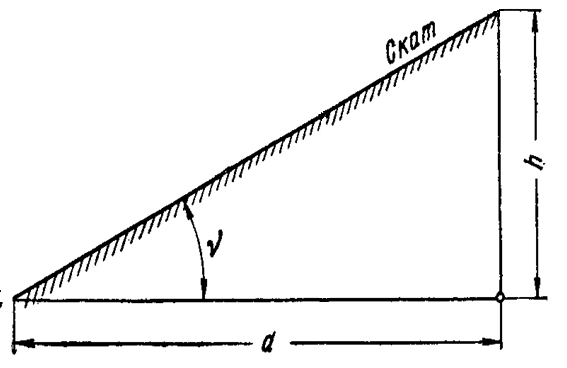
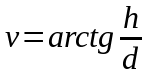
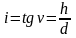
Уклон линии выражают в тысячных долях, процентах и промилле.

Например: h =1м, d =200м, тогда i=1/200 =0,005 =0,5% =5‰

чтобы избежать расчетов при определении крутизны скатов по плану или карте, пользуются специальными графиками, называемыми графиками заложений.

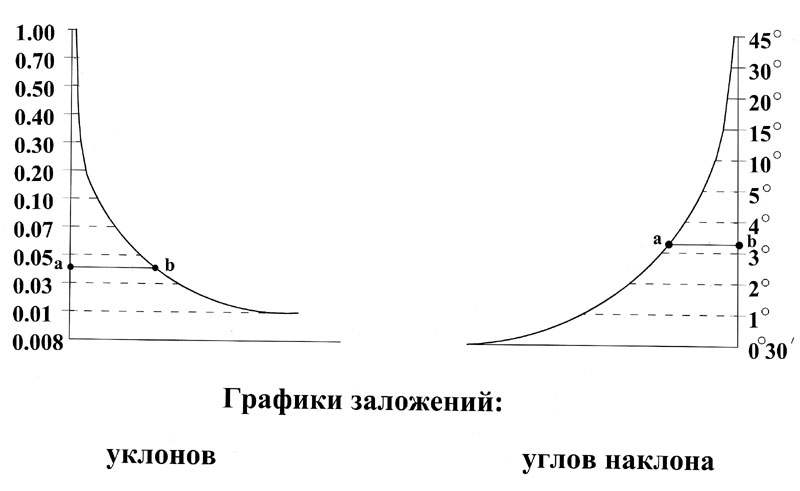
15.Определение площади по планам и картам.

Определение площадей по плану или карте

Способ определения

площади с разбивкой участка

на геометрические фигуры

Способы определения площадей с помощью палеток

а – квадратной; б – линейно

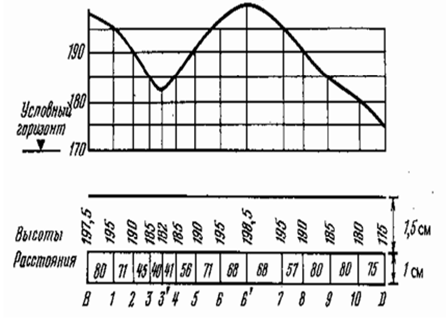
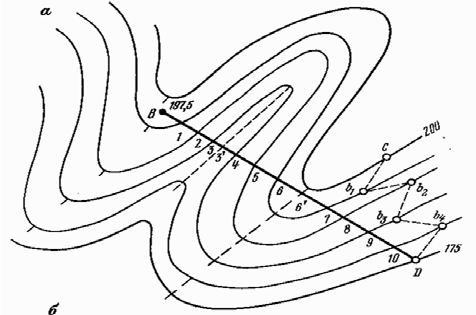
16. Построение продольного профиля по линии на карте, плане.

Для построения профиля по линии ВD (рис. а) на листе бумаги проводят горизонтальную линию, на ней в масштабе плана последовательно откладывают отрезки B–1, 1–2; 2–3, 3–3′...10-D, (точки пересечения линии профиля с горизонталями), выписывают их абсолютные отметки. В каждой из полученных точек восстанавливают перпендикуляры (рис. б) и на них в принятом вертикальном масштабе откладывают профильные отметки, равные разности абсолютных отметок точек и условного горизонта, т. е. Условный горизонт (УГ) выбирают таким образом, чтобы его линия не пересекалась с линией профиля (например, УГ = 170 м). Соединив концы перпендикуляров плавной кривой, получают профиль местности по линии BD.

17.Что понимают под погрешностью измерений. Абсолютная и относительная погрешность.

Погрешность измерений – это отклонение результатов измерения от истинного значения измеряемой величины.

Абсолютная погрешность – это погрешность, выражаемая в единицах измеряемой величины.

Относительная погрешность является отвлеченным числом и выражается чаще всего в виде простой дроби с числителем, равным единице, отношение абсолютной погрешности к значению измеряемой величины.

Измерения в геодезии рассматриваются с двух точек зрения: количественной, выражающей числовое значение измеренной величины, и качественной, характеризующей ее точность.

Из практики известно, что даже при самой тщательной и аккуратной работе многократные (повторные) измерения не дают одинаковых результатов. Это указывает на то, что получаемые результаты не являются точным значением измеряемой величины, а несколько отклоняются от него. Значение отклонения характеризует точность измерений

Относительная ошибка

В практике геодезических измерений о точности измерений судят не только по абсолютной величине средней квадратической или предельной погрешности, но и по величине относительной погрешности.

Относительной ошибкой называется отношение абсолютной ошибки к значению самой измеренной величины.

Относительную ошибку выражают в виде простой дроби, числитель которой — единица, а знаменатель — число, округленное до двух - трех значащих цифр с нулями.

Δ_отн = т_l /l =1/(l / т_l ),

где l - значение измеряемой величины.

Относительная предельная ошибка:

Δ_{отн. пр.} = Δ_пр / l, где Δ_пр = 2(3)m

18.Что такое грубые, случайные и систематические погрешности

Грубые ошибки резко отклоняют результаты измерений от истинного значения измеряемой величины. Это в основном промахи и просчеты исполнителя. Грубые погрешности обнаруживают путем повторения измерения и сравнения их результатов. Если расхождения между результатами превосходят заданный допуск, то эти измерения выбраковывают и производят заново.

Систематические ошибки входят в каждый результат измерений по определенному закону, однообразно повторяются в многократных измерениях. Систематические погрешности удается исключить или свести их до минимума тщательной проверкой измерительных приборов, применением соответствующей методики измерений , а также введением поправок в результаты измерений.

Случайные ошибки – это ошибки, размер и влияние которых на каждый отдельный результат измерения остается неизвестным. Закономерности случайных ошибок проявляются в массе, то есть, при большом количестве измерений; такие закономерности называют статистическими. Случайные ошибки подчинены определенным вероятностным закономерностям, изучение которых дает возможность получить наиболее надежный результат и оценить его точность. Теория ошибок занимается в основном изучением случайных ошибок.

19.Равноточные и неравноточные измерения

Результаты геодезических измерений в своей группе могут быть равноточными и неравноточными.

Если измерения выполнены прибором одного и того же класса точности, по одной и той же методике (программе), в одинаковых внешних условиях, одним и тем же наблюдателем (либо наблюдателями одной квалификации), то такие измерения относят к равноточным. При несоблюдении хотя бы одного из перечисленных выше условий результаты измерений классифицируют как неравноточные.

Примером равноточных измерений могут являться результаты измерений длины одной и той же линии либо линий, примерно равных друг другу, полученные при неизменных условиях внешней среды, одним и тем же измерительным средством (прибором), одними и теми же исполнителями работ, по общей для всех результатов измерений программе.

Если в процессе измерений длины линии, например, светодальномером, изменится температура окружающего воздуха, влажность, давление, то это может привести к получению части неравноточных результатов в общей группе результатов измерений, поскольку при изменении внешних условий может произойти и изменение характеристик измерительного прибора, характеристик прохождения светового луча в атмосфере.

20.Перечислить основные свойства случайных погрешностей

Свойства случайных ошибок

1. При определенных условиях измерений случайные ошибки по абсолютной величине не могут превышать известного предела, называемого предельной ошибкой. Это свойство позволяет обнаруживать и исключать из результатов измерений грубые погрешности.

2. Положительные и отрицательные случайные погрешности примерно одинаково часто встречаются в ряду измерений, что помогает выявлению систематических погрешностей.

3. Чем больше абсолютная величина погрешности, тем реже она встречается в ряду измерений.

4. Среднее арифметическое из случайных погрешностей измерений одной и той же величины, выполненных при одинаковых условиях, при неограниченном возрастании числа измерений стремится к нулю. Это свойство, называемое свойством компенсации, можно математически записать так:

5.Последнее свойство случайных ошибок позволяет установить принцип получения из ряда измерений одной и той же величины результата наиболее близкого к её истинному значению. Таким результатом является среднее арифметическое из измеренных значений данной величины.

21.Как определить среднюю квадратическую погрешность (формулы Гаусса и Бесселя).

Средняя квадратическая , предельная и относительная ошибки

Средняя квадратическая ошибка m введена в теорию ошибок для характеристики точности отдельного измерения

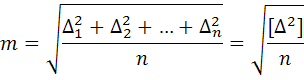где n — число измерений данной величины.

Формула (1), которую называют формулой Гаусса, применима для случаев, когда известно истинное значение измеряемой величины Х. Такие случаи в практике встречаются редко. В то же время из измерений можно получить результат, наиболее близкий к истинному значению, — арифметическую середину. Для этого случая средняя квадратическая погрешность одного измерения подсчитывается по формуле Бесселя:

где _i= l_i – X_o

— отклонения отдельных значений измеренной величины от арифметической средины, называемые вероятнейшими ошибками, причем [] = 0.

22.Виды нивелирования, физические основы.

Геометрическое нивелирование заключается в непосредственном определении разности высот точек с помощью горизонтального оптического визирного луча, задаваемого при помощи нивелира.

(горизонтальным лучом - нивелиром)

Тригонометрическое нивелирование заключается в определении превышений между точками по измеренному между ними расстоянию и углу наклона. Вычисление превышений ведут по формулам тригонометрии. (наклонным лучом - теодолитом )

Физическое нивелирование делится на три вида:

• гидростатическое, основанное на свойстве свободной поверхности жидкости в сообщающихся сосудах всегда находиться на одинаковом уровне независимо от превышения точек, на которых установлены эти сосуды; (сообщающиеся сосуды)

• барометрическое, в основу которого положена зависимость между величиной атмосферного давления на точке местности и ее высотой. Современные приборы барометрического нивелирования позволяют определять отметки точек с точностью 0,5 м и выше; (барометром-анероидом)

• радиолокационное нивелирование производят с летательных аппаратов посредством определения длины пути прохождения электромагнитных волн отраженных от земной поверхности.

• Механическое нивелирование производят с помощью специальных приборов (профилографов - автоматов), устанавливаемых на велосипедных рамах, автомобилях и т. д. При движении такого прибора автоматически регистрируются пройденные им расстояния, высоты точек и вычерчивается профиль пройденного пути.

• Стереофотограмметрическое нивелирование основано на определении превышений по паре фотоснимков одной и той же местности, полученных из двух точек базиса фотографирования.

23.Сущность геометрического нивелирования. . Сущность геометрического нивелирование заключается в следующем нивелир устанавливают горизонтально и по рейкам с делениями, стоящими на точках a и b, определяют превышение h как разность между отрезками a и b. Если известно отметка 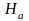, точки a и превышение h, отметку 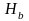, в точке в определяют как их сумму. .

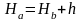24. Способы нивелирования из середины и вперед. Порядок измерения превышения на станции.

1 8. В чем сущность нивелирования из середины и его точность.

Нивелирование с середины (простое). Для определения между точками А и В достаточно один раз установить нивелир, такой случай называется простым нивелированием. Превышение h определяют как разность между отрезками a и b: h=a-b. Если известна отметка точки А и превышение h, отметку Н_b точки В определяют как их сумму .

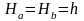При этом способе превышение между точками не зависит от высоты нивелира над землей.

В чем сущность нивелирования вперед и его точность

П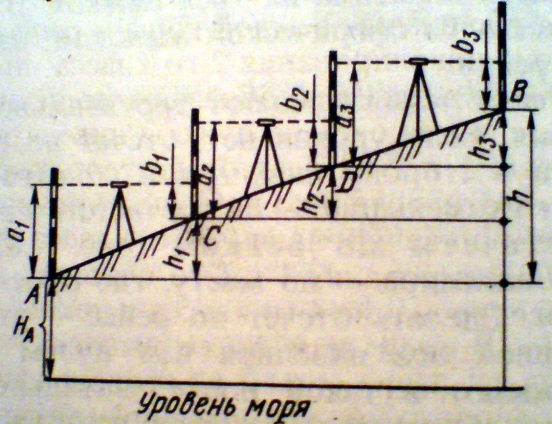 ревышение между точками можно определить только после нескольких установок нивелира, такое нивелирование условно называют сложным. В этом случае точки Д и С называются связующими. Превышение между ними определяют по схеме простого нивелирования. При сложном нивелировании превышение между точками А и В: 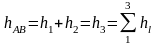. Если известна отметка точки А, можно определить отметку точки В: 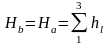. Такую схему нивелирования называют нивелирным ходом.

При этом способе оба отсчета a и b будут больше на одну и ту же величину, но разность между ними будут одинаковыми.

25.Что такое горизонт нивелира. Как вычислить отметки точек через горизонт нивелира.

В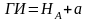 еличина H_i, называется горизонтом прибора (ГП) или горизонтом инструмента (ГИ) и, как это видно из рисунка, является высотой визирного луча над исходной уровенной поверхностью. Следовательно, горизонт прибора на данной станции равен отметке точки плюс отсчет по рейке, установленной в этой точке.

О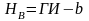 тсюда, отметка точки равна горизонту прибора минус отсчет по установленной в ней рейке:

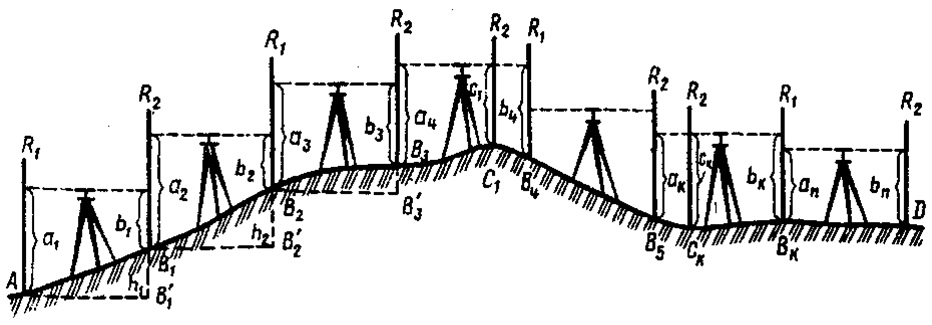
26.Понятие о нивелирном ходе: связующие и промежуточные точки.

Процесс измерения превышений одних точек относительно других на местности называется нивелированием. Геометрическое нивелирование или нивелирование горизонтальным лучом выполняется специальным прибором – нивелиром; отличительная особенность нивелира состоит в том, что визирная линия трубы во время работы приводится в горизонтальное положение.

Точки, общие для двух соседних станций, называются связующими, например В₁, В₂, В₃, В₄. Точки, расположенные между связующими, называются промежуточными, например C₁ и С_К. Такие точки служат для получения отметок характерных изломов местности.

27.Что такое тригонометрическое нивелирование и его точность.

Тригонометрическое нивелирование выполняется теодолитом или тахеометром; для определения превышения между двумя точками нужно измерить ν - угол наклона и d – горизонтальное проложение.

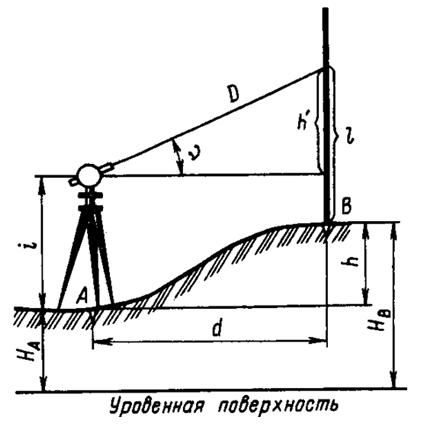
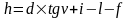где f – поправка за кривизну земли и рефракцию, её вводят при d>300 метров

Ошибка измерения превышения от 2 см до 10 см на 100 м расстояния.

28.Технический нивелир: устройство, геометрические условия основных осей.

Нивелир – геодезический прибор, предназначенный для измерения превышения между двумя точками при помощи горизонтального визирного луча и вертикально установленных в этих точках реек.

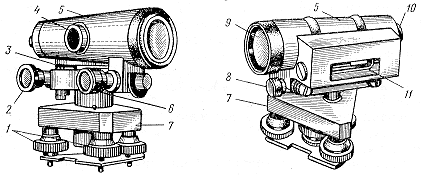а – вид со стороны круглого уровня; б – вид со стороны цилиндрического уровня:

1 – подъемные винты; 2 – элевационный винт; 3 – круглый уровень; 4 – кремальера; 5 – корпус зрительной трубы; 6 – наводящий винт; 7 – трегер; 8 – закрепительный винт; 9 – объектив; 10 – окуляр с диоптрийным кольцом; 11 – контактный цилиндрический уровень.

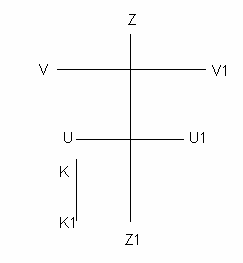ZZ₁ – ось вращения прибора,

VV₁ – визирная ось зрительной трубы,

КК1 – ось круглого уровня,

UU1 – ось цилиндрического уровня

29.Как выполняется поверка и юстировка круглого уровня нивелира

Ось круглого уровня должна быть параллельна оси вращения инструмента. Для поверки этого условия подъемными винтами приводят пузырек круглого уровня в центр ампулы и поворачивают верхнюю часть нивелира на 180°. Если после этого пузырек останется в центре ампулы, то условие выполнено. В противном случае исправительными винтами круглого уровня перемещают пузырек к центру на половину дуги отклонения и окончательно совмещают пузырек уровня с центром ампулы с помощью подъемных винтов. Поверку повторяют до полного выполнения требуемого условия.

30.Как выполняется поверка и юстировка сетки нитей нивелира

Вертикальная нить сетки должна быть параллельна оси нивелира. В защищенном от ветра месте подвешивают отвес. В 20 — 25 м от отвеса устанавливают нивелир, приводят его по круглому уровню в рабочее положение и совмещают один из концов вертикальной нити со шнуром отвеса. Если другой конец нити отклоняется от шнура не более 0,5 мм, то условие выполнено.

Если условие нарушено, то, ослабив крепежные винты, пластинку с сеткой нитей поворачивают до совмещения вертикальной нити со шнуром отвеса.

31.Как выполняется поверка и юстировка главного условия нивелира

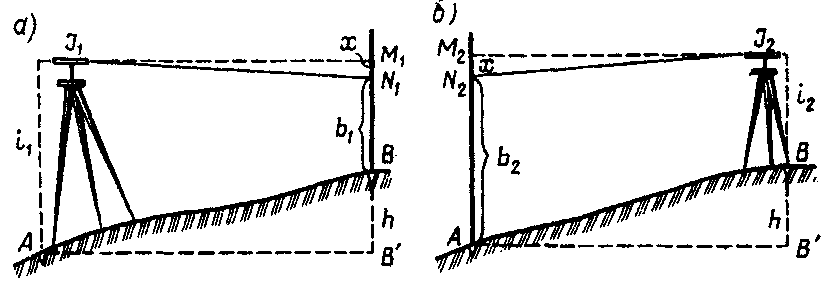
3. Визирная ось зрительной трубы должна быть параллельна оси цили-ндрического уровня. Это условие часто называют главным условием нивелира. Проверяют его двойным нивелированием одного и того же отрезка линии. С этой целью закрепляют колышками линию АВ (рис.) длиной 50 — 75 м. Нивелир устанавливают на станции (рис. а) так, чтобы окуляр находился над точкой А, и измеряют высоту инструмента i₁ , а по рейке, установленной в точке В, берут отсчет b₁. Затем нивелир и рейку меняют местами (рис. б), измеряют высоту инструмента i₂ и берут отсчет по рейке B₂.

32.Принцип измерения горизонтальных и вертикальных углов.