
- •7. Внутренняя энергия термодинамической системы.Изменение внутренней энергии.Энтальпия
- •Энтальпия
- •8. Теплоемкость газа. Виды теплоемкости. Уравнение Майера
- •9. Сушность первого закона термодинамики. Аналитическое выражение первого закона термодинамики.
- •10. Последовательность и обьем расчета термодинамических процессов
- •11. Определение, осуществление и исследование основных термодинамических процессов
- •12 Обобщающее значение политропных процесссов
- •13. Круговые процессы(циклы) Прямые и обратные
- •14 Цикл Карно и теорема Карно
12 Обобщающее значение политропных процесссов
политропный процесс – это термодинамический процесс, при осуществлении которого может изменяться любой из параметров состояния (p, υ, T), а также возможен теплообмен с окружающей средой.
Примерами политропных процессов могут служить процессы сжатия и расширения рабочего тела в ГТД с учётом сил трения.
1. Уравнение процесса: p·υn = const, где n показатель политропы. Показатель n может быть любым числом (–∞ < n < +∞), следовательно, политропных процессов бесконечное множество. Но в каждом конкретном процессе величина n постоянна.
2. Поскольку уравнение политропного процесса совпадает по форме с адиабатным, то легко можно получить соотношения между параметрами в начале и в конце политропного процесса
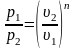 ;
;
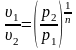
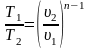 ;
;
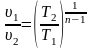
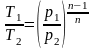 ;
;
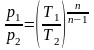
.
Определение величин, входящих в первый закон термодинамики
а) qn = Сn·(T2 – T1),
где Сn – теплоёмкость газа в политропном процессе.
б) –∆U = Cυ·(T2 – T1)
в) Ln
=
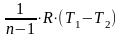 .
.
Это уравнение по форме одинаково с соответствующим уравнением для адиабатного процесса и отличается от него только значением показателя политропы n.
Найдём формулу для вычисления Сn в произвольном политропном процессе. Для этого подставим в уравнение первого закона термодинамики величины qn, ∆U, Ln их аналитическое выражение. В результате получим:
qn = ∆U + Ln
Сn·∆T
= Cυ·∆T
+
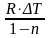
Сn
= Cυ
+
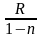 или Сn
= Cυ
·
или Сn
= Cυ
·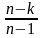 . (3.54)
. (3.54)
Из этого выражения видно, что если считать теплоёмкость Cυ не зависящей от температуры, то Сn для идеального газа в политропном процессе будет постоянна и её можно всегда найти, зная Cυ, R и n.
4. Каждому политропному процессу соответствует своё распределение энергии. Поскольку таких процессов множество, исследовать их все не представляется возможным. Однако качественное суждение о характере распределения энергии в любом политропном процессе можно сделать, рассмотрев его расположение по отношению к известным нам процессам: изохорному, изобарному, изотермическому и адиабатному, которые являются частными случаями политропных процессов. Уравнение каждого из них можно представить в виде p·υn = const со своим значением показателя политропы.
Действительно, при n = 0 уравнение политропы получает вид:
p·υ° = p·1 = const или p = const (изобарный процесс).
При n = 1 уравнение политропы описывает изотермический процесс:
p·υ1 = p·υ = const.
При n = k, политропы совпадают с адиабатой:
p·υk = const.
13. Круговые процессы(циклы) Прямые и обратные
Совокупность термодинамических процессов, в результате которых рабочее тело возвращается в первоначальное состояние, называется круговым процессом или циклом.
Циклы имеют большое практическое значение, так как они позволяют осуществлять превращение теплоты в работу, а также непрерывную передачу теплоты с низшего температурного уровня на высший.
Если за цикл совершается положительная работа A>0 (цикл протекает по часовой стрелке), то он называется прямым (если за цикл совершается отрицательная работа A<0 (цикл протекает против часовой стрелки), то он называется обратным
Перейдём к рассмотрению кругового процесса теплового двигателя

Рис.4.1. Круговой процесс (цикл) теплового двигателя: а – изображение прямого цикла в рабочей диаграмме, б – изображение прямого цикла в тепловой диаграмме, в – осуществление кругового процесса
