10. Последовательность и обьем расчета термодинамических процессов

В тепловых двигателях при их работе протекают разнообразные термодинамические процессы. Целью изучения термодинамических процессов является установление закономерностей изменения параметров состояния ТДС и особенностей преобразования энергии в этих процессах.

Знание указанных закономерностей имеет важное значение для понимания процессов, протекающих в элементах ГТД и ДВС.

Анализ (или расчёт) термодинамических процессов производится обычно в следующей последовательности:

1. Определяют уравнение процесса: исходя из условий протекания процессов и используя уравнение состояния идеального газа, находят уравнения процесса в виде зависимостей

p = f (υ); T = f (υ); T = f (p).

2. Определяют закон изменения параметров на основании уравнения процесса и уравнения состояния, используя известные по условиям задачи значения параметров состояния в начале процесса (p₁, υ₁, T₁), в конце процесса (p₂, υ₂, T₂), а если требуется – то и в промежуточных состояниях.

3. Осуществляют графическое построение процесса в рабочей “p-υ” диаграмме и тепловой “T-s” диаграмме.

4. Определяют величины, входящие в первый закон термодинамики.

q = ∆U + L; T∙∆s = ∆U + pdυ

а) q = ;

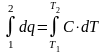б) ∆U = ;

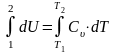в) L = ;

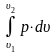г) ∆s_1-2 = 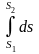= s₂ – s₁.

5. Определяют закон распределения энергии (α) для данного процесса по формуле α = ∆U/q.

Все величины, указанные в пунктах 2 и 4 могут, найдены как аналитически по уравнениям, так и графически с помощью рабочей “p-υ” диаграммы и тепловой “T-s” диаграммы. Поэтому любой расчёт процесса всегда сопровождается графическим построением процесса в этих координатах.

11. Определение, осуществление и исследование основных термодинамических процессов

Основными процессами в термодинамике являются:

• изохорный, протекающий при постоянном объеме;

• изобарный, протекающий при постоянном давлении;

• изотермический, происходящий при постоянной температуре;

• адиабатный, при котором теплообмен с окружающей средой отсутствует;

• политропный, удовлетворяющий уравнению pvⁿ= const.

Изохорный, изобарный, изотермический и адиабатный процессы являются частными случаями политропного процесса.

При исследовании термодинамических процессов определяют:

• уравнение процесса в p-v, иT-sкоординатах;

• связь между параметрами состояния газа;

• изменение внутренней энергии;

• величину внешней работы;

• количество подведенной теплоты на осуществление процесса или количество отведенной теплоты.

При изохорном процессе выполняется условие v = const.

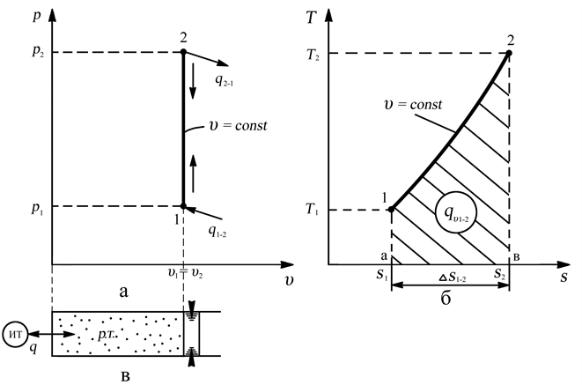Из уравнения состояния идеального газа (pv = RT) следует:

•  p/T = R/v = const,

т. е. давление газа прямо пропорционально его абсолютной температуре:

•  p₂/p₁ = T₂/T₁. 

Работа расширения в изохорном процессе равна нулю (l = 0), так как объем рабочего тела не меняется (Δv = const).

Количество теплоты, подведенной к рабочему телу в процессе 1-2 при c_v = const определяется по формуле:

• q= c_v(T₂ -  T₁). 

Т. к.l = 0, то на основании первого закона термодинамики Δu = q, а значит изменение внутренней энергии можно определить по формуле:

• Δu = c_v(T₂ — T₁).

Изменение энтропии в изохорном процессе определяется по формуле:

• s₂ – s₁= Δs = c_vln(p₂/p₁) = c_vln(T₂/T₁). 

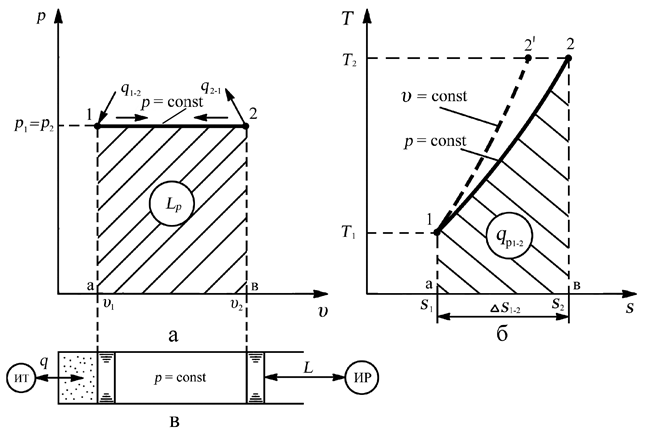
Изобарным называется процесс, протекающий при постоянном давлении p = const. Из уравнения состояния идеального газа слуедует:

v/T = R/p = const

или

v₂/v₁ = T₂/T₁,

т. е. в изобарном процессе объем газа пропорционален его абсолютной температуре.

Работа будет равна:

l = p(v₂ – v₁). 

Т. к. pv₁ = RT₁ и pv₂ = RT₂, то

l = R(T₂ – T₁).

Количество теплоты при c_p = const определяется по формуле:

q = c_p(T₂ – T₁). 

Изменение энтропии будет равно: 

s₂ – s₁= Δs = c_pln(T₂/T₁).

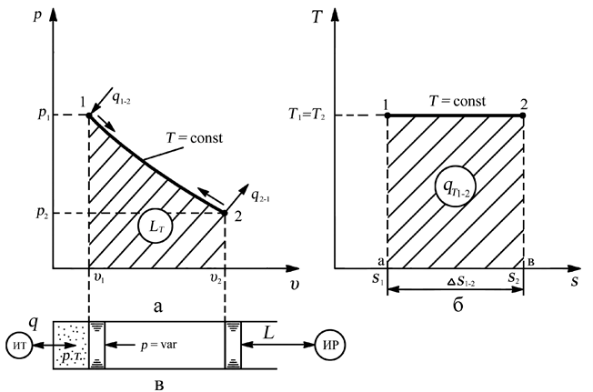
При изотермическом процессе температура рабочего тела остается постоянной T = const, следовательно:

pv = RT = const

или

p₂/p₁ = v₁/v₂, 

т. е. давление и объем обратно пропорциональны друг другу, так что при изотермическом сжатии давление газа возрастает, а при расширении – снижается.

Работа процесса будет равна:

l  = RTln (v₂ – v₁) = RTln (p₁ – p₂).

Так как температура остается неизменной, то и внутренняя энергия идеального газа в изотермическом процессе остается постоянной (Δu = 0) и вся подводимая к рабочему телу теплота полностью превращается в работу расширения:

q = l.

При изотермическом сжатии от рабочего тела отводится теплота в количестве, равном затраченной на сжатие работе.

Изменение энтропии равно:

s₂ – s₁= Δs = Rln(p₁/p₂) = Rln(v₂/v₁).

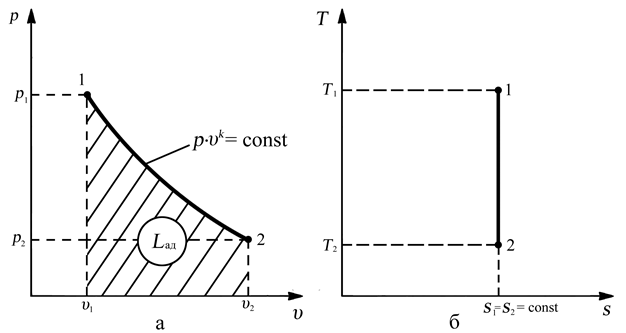
Адиабатным называется процесс изменения состояния газа, который происзодит без теплообмена с окружающей средой. Так как dq = 0, то уравнение первого закона термодинамики для адиабатного процесса будет иметь вид:

du + pdv = 0

или

Δu+ l = 0,

следовательно

Δu= -l. 

В адиабатном процессе работа расширения совершается только за счет расходования внутренней энергии газа, а при сжатии, происходящем за счет действия внешних сил, вся совершаемая ими работа идет на увеличение внутренней энергии газа.

Обозначим теплоемкость в адиабатном процессе через c_ад, и условие dq = 0 выразим следующим образом:

dq = c_адdT = 0. 

Это условие говорит о том, что теплоемкость в адиабатном процессе равна нулю (c_ад = 0).

Известно, что

с_p/c_v = k 

и уравнение кривой адиабатного процесса (адиабаты) в p, v-диаграмме имеет вид:

pv^k = const. 

В этом выражении k носит название показателя адиабаты (так же ее называют коэффициентом Пуассона).