1.4. Охолодження (нагрівання) необмеженої пластини

Н

Рис. 4.6. Охолодження необмеженої пластини в середовищі з постійною температурою.

ехай необмежена пластина товщиною 2 і з рівномірною початковою температурою занурюється в середовище з постійною температурою . Коефіцієнт тепловіддачі  на поверхні пластини постійний. Необхідно визначити температуру в будь-якій точці пластини в довільний момент часу (рис. 4.6).

Якісний аналіз такої задачі дозволяє затверджувати:

1. Задача симетрична, і при профіль температури є дзеркальним відображенням профілю при позитивних х. При цьому очевидно, що на осі пластини похідна температури і, отже, тепловий потік обертається в нуль.

2. Розв’язок задачі повинен бути достатньо складним, оскільки температурне збурення поступово охоплює всю товщину пластини (див. рис. 4.6).

Математичне формулювання задачі складається з диференціального рівняння теплопровідності

з початковою

,

та з граничними умовами

(4.21)

Введемо в розгляд безрозмірні величини, що дозволять скоротити число змінних і додати узагальненість розв’язку задачі:

.

Тоді диференціальне рівняння теплопровідності перепишеться у вигляді

або

, (4.22)

де - безрозмірний час. Умови однозначності (4.21) приймають вигляд

(4.23)

.

Комплекс носить назву числа (критерію) Біо і є відношенням внутрішнього термічного опору до зовнішнього, тобто .

Шукана функція Θ залежить як від часу, так і від координати, так що . Припустимо, що ця функція може бути представлена у вигляді добутку двох інших функцій, кожна з яких залежить тільки від однієї змінної:

. (4.24)

Цей метод розв’язання носить назву методу розподілу змінних Фур’є. Використовуючи (4.24), обчислимо похідні

Підставляючи одержаний результат в диференціальне рівняння теплопровідності (4.22), маємо

Оскільки х і – незалежні змінні, ліва частина повинна залежати тільки від х, а права – тільки від . Це можливо тільки в тому випадку, якщо обидва записаних відношення сталі:

. (4.25)

Вибір константи у вигляді означає, що вона завжди має від’ємне значення. Це безпосередньо випливає з фізичних міркувань, оскільки температура падає з часом і її похідна при цьому . Рівняння (4.25) розпадається на два звичайні лінійні диференціальні рівняння

розв’язками яких служить, відповідно,

Остаточно загальний розв’язок рівняння (1.22) має вигляд

(4.26)

Приступимо тепер до визначення постійних інтегрування. Легко передбачити, що А=0, оскільки умова симетрії температурного профілю припускає, що функція повинна бути парною. Цей же висновок може бути одержаний шляхом формального задоволення умови .

Тоді

. (4.27)

Задовольнимо тепер другу граничну умову (4.23): при Х=1

.

Звідси

. (4.28)

Це співвідношення, що називають характеристичним рівнянням, визначає величину μ як функцію числа Bi. Рівняння (4.28) є трансцендентним, тому його розв’язок може бути знайдено будь-яким наближеним способом, у тому числі і графічно (рис. 4.7)

З графіка видно, що рівняння (4.28) має незліченну безліч розв’язків . Оскільки рівняння (4.22) є лінійним, його загальний розв’язок є суперпозицією всіх частинних:

(4.29)

Визначимо лише величину B_n. Скористаємося для цього початковою умовою (4.23)

. (4.30)

Р івняння (4.30) є розкладом одиниці в ряд Фур’є по косинусах. Визначення B_n не складає складнощів, для цього достатньо помножити обидві частини (4.30) на і проінтегрувати в межах від 0 до 1:

Рис. 4.7. Графічний розв’язок характеристичного рівняння (4.28)

. (4.31)

Відомо, що функція є ортогональною. Це означає, що

Обчислюючи вказаний інтеграл для випадку m = n, отримаємо

.

Підставляючи цей результат в (4.31) і обчислюючи інтеграл в лівій частині, маємо

,

звідки

. (4.32)

Таким чином, остаточний розв’язок поставленої задачі приймає вигляд

, (4.33)

де μ_n визначається з рівняння (4.28).

А

Рис. 4.8. Зміна профілю температури в плоскій стінці при її охолодженні. Направляюча точка.

наліз розв’язку. Отриманий розв’язок, як і очікувалося, виявилося досить громіздким. Проте, в багатьох практично важливих випадках воно допускає значні спрощення. Перш за все вкажемо, що при ряд (4.23) настільки швидко сходиться, що для обчислення безрозмірної температури Θ цілком можна обмежиться першим членом розкладу

. (4.34)

Для фіксованої координати очевидно .

З метою полегшення практичних розрахунків для характерних точок (середина пластини, поверхня) в спеціальних довідкових виданнях містяться графіки функції . З (4.34) також витікає, що при просторова залежність Θ описується функцією косинуса, а часова – експонентою.

Вплив числа Bi, тобто умов теплообміну, зручно проілюструвати графічно за допомогою правила направляючої точки. Виявляється, що у будь-який момент часу дотичні до температурної кривої, проведені в точці Х=1, перетинаються в одній і тій же точці N, яка носить назву направляючої (рис. 4.8). З рисунка видно, що , але водночас ; отже:

. (4.35)

Я

Рис. 4.9. Зміна температури при охолодженні плоскої стінки при умові

кщо рівняння (4.35) порівняти з відповідною граничною умовою (4.23), то можна встановити, що . Таким чином, положення направляючої точки не змінюється з часом і залежить тільки від числа Bi. Зокрема при направляюча точка зміщується в нескінченність, а при виявляється на поверхні тіла. Оскільки обидва ці граничні випадки викликають особливу цікавість, розглянемо їх детальніше.

1. (практично Bi < 0.1). Умова рівнозначна твердженню . Інакше кажучи, стік тепла в даному випадку лімітується термічним опором тепловіддачі. Тому розподіл температури в пластині у будь-який момент часу є рівномірним (рис. 4.9).

Насправді, якщо , то (рис. 4.8) і всі коефіцієнти ряду (4.33), окрім першого, обертаються в нуль. Це випливає з рівняння (4.32). Що стосується першого коефіцієнта, то

.

Характеристичне рівняння (4.28) приймає вигляд , крім того, ясно, що при . Тоді з (4.33) слідує

, (4.36)

або в розмірній формі

. (4.37)

Підкреслимо, що при отриманні цих співвідношень умова не ставилося, тобто для температурна залежність від часу, починаючи з початку процесу охолоджування, описується простою експонентою.

2

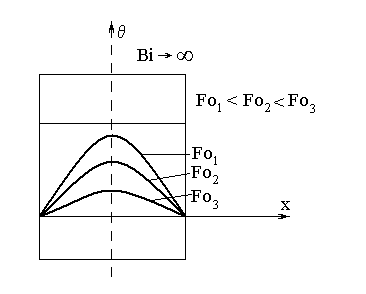
Рис. 4.10. Зміна температури при охолодженні плоскої стінки при умові

. (практично Bi > 100). Ця умова фізично означає, що на поверхні пластини відбувається інтенсивний відбір тепла або теплопровідність пластини дуже мала, тобто . В цих умовах температура поверхні практично миттєво падає до температури охолоджуючого середовища, так що протягом всього процесу теплообміну (рис. 4.10). Знайдемо розподіл температури в пластині, коли і можна обмежитися першим членом розкладу (4.33).

При ,

.

Розподіл температури приймає наступний вигляд:

. (4.38)

Неважко переконатися, що на поверхні (x = ) Θ = 0. На вісі пластини (x = 0)

. (4.39)

Рівняння (4.39) виявляється досить простим, як і (4.36), і дозволяє аналітично вирішити не тільки пряму, але і зворотну задачу – визначати час, необхідний для охолодження (прогрівання) пластини до заданої температури.