3. Нагрів (охолоджування) напівобмеженого масиву. Граничні умови 2-го роду.

Необхідно встановити розподіл температури в рівномірно прогрітому до температури напівобмеженому масиві, до поверхні якого підводиться постійний тепловий потік (рис. 4.4).

Математичне формулювання задачі:

;

; (4.10)

,

Для розв’язку виявляється зручним перехід від температури до теплового потоку, для чого достатньо продиференціювати диференціальне рівняння теплопровідності по координаті і домножити обидві його частини на –:

Рис. 4.4. Нестаціонарна теплопровідність в напівобмеженому масиві з граничними умовами ІІ-го роду.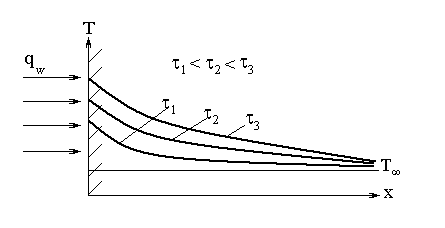

.

Враховуючи, що і ввівши нову змінну , одержимо

(4.11)

з початковою умовою

,

і граничними умовами

(4.12)

У такій постановці задача повністю аналогічна розглянутій в попередньому параграфі (див. рів. (4.2а) – (4.4а)). Отже, її розв’язок може бути записаний відразу:

. (4.13)

Тепер необхідно зробити зворотній перехід – від теплового потоку до температури. З одного боку:

,

З іншого:

.

Прирівнюючи праві частини і інтегруючи, одержимо

.

Інтеграл береться по частинах по формулі Ньютона – Лейбніца так, що

.

Тоді

.

Задовольнимо умові , помітимо при цьому, що при . Звідси витікає, що . Остаточно матимемо

. (4.14)

Перепад температур на поверхні

(4.16)

Таким чином, температура поверхні росте пропорційно кореню квадратному від часу.

Тепер встановимо, яким чином в цьому випадку розповсюджується фронт температурного збурення. Приведемо (4.15) до безрозмірного вигляду

. (4.17)

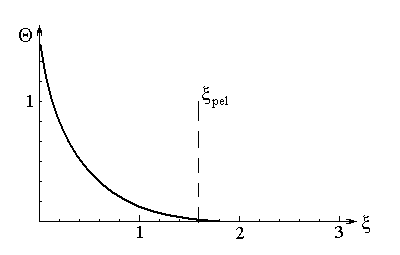
Вид функції показаний на рис. 4.5. Величина досягає значення 0,01 при . Це означає, що

. (4.18)

Т

Рис. 4.5. Залежність безрозмірної температури від параметра

аким чином, характер граничної умови впливає на швидкість переміщення фронту. При постійній температурі поверхні вона виявляється декілька вищою, ніж для випадку постійного теплового потоку.

На закінчення цього розділу покажемо, що одержані рішення, які вимагали ретельних і досить довгих математичних викладок, можна досить легко знайти, виходячи з простих фізичних міркувань. Насправді, для випадку тепловий потік на границі може бути оціненим як

,

якщо замінити похідну відношенням кінцевих різниць. Тут – деякий характерний лінійний розмір, який з умов задачі може бути представлений тільки у вигляді комбінації . Тоді

, (4.19)

що відрізняється від точного рішення (4.9) на коефіцієнт .

Аналогічна оцінка для температури поверхні у випадку дає

, (4.20)

яка відрізняється від точного рішення (4.16) на коефіцієнт .