Розділ 4. Нестаціонарна теплопровідність

4.1. Класифікація процесів

При розв’язуванні багатьох практичних задач розрахунку температурних полів різних конфігурацій доводиться досліджувати нестаціонарний процес теплопровідності в полях різної форми. Процеси теплопровідності, коли поле температур змінюється не тільки в просторі, але і в часі називають нестаціонарними. Такі процеси виникають в тілі при зменшенні умов його теплообміну з навколишнім середовищем або потужності енерговиділення внутрішніх джерел теплоти, які можуть діяти в об'ємі тіла .

Серед практичних задач нестаціонарної теплопровідності найважливіше значення мають дві групи процесів:

a) тіло прагне до теплової рівноваги;

b) температура тіла зазнає періодичних змін.

До першої групи відносяться процеси прогрівання або охолодження тіл, поміщених в середовище з заданим тепловим станом.

До другої групи відносяться процеси в періодично діючих підігрівачах. В міру нагрівання температура в кожній точці асимптотика наближається до температури нагріваючого середовища. Найшвидше змінюється температура точок, що лежать поблизу поверхні тіла. З часом ця різниця зменшуватиметься і теоретично через достатньо великий відрізок часу вона буде рівною нулю.

В умовах передачі теплоти через стінку при раптовій зміні температури одного з теплоносіїв не вся теплота передаватиметься через стінку: частина її піде на зміну внутрішньої енергії самої стінки (її температури), і лише при встановленні стаціонарного процесу вся теплота передаватиметься через стінку від однієї речовини до іншої.

Приведені приклади вказують на те, що нестаціонарні теплові процеси завжди пов'язані зі зміною внутрішньої енергії або ентальпії речовини.

В

Рис. 4.1 Класифікація процесів нестаціонарної теплопровідності

ивчимо процеси теплопровідності, в яких температура залежить від часу, тобто . Рівняння теплопровідності, що описує такі процеси, якщо фізичні властивості постійні і відсутні внутрішні джерела тепла, має вид рівняння (4.1):

. (4.1)

Існує три типи задач нестаціонарної теплопровідності залежно від характеру часової залежності температури (рис. 4.1):

1. Перехідні процеси. Температура змінюється від одного значення до іншого (рис. 4.1, а).

2. Безперервне нагрівання (охолодження) (рис. 4.1, б). Звичайно, це не потрібно розуміти так, що температура може рости або знижуватися безмежно. Тут мається на увазі те, що нас цікавить ділянка температурної кривої, коли температура не прагне до якогось певного значення.

3. Періодичні процеси. Температура коливається біля деякого середнього значення (мал. 4.1, в).

4.2. Нагрів (охолоджування) напівобмеженого масиву. Граничні умови 1-го роду.

Рис. 4.2. Нестаціонарна теплопровідність в напівобмеженому масиві з граничними умовами І роду.

У задачі необхідно встановити розподіл температури в рівномірно прогрітому до температури напівобмеженому масиві, на поверхні якого температура стрибком піднялася до (рис. 4.2).

Диференціальне рівняння теплопровідності в цьому випадку має вигляд

(4.2)

з початковими

(4.3)

і граничними умовами

(4.4)

Введемо в розгляд безрозмірну температуру . Тоді система рівнянь (4.3) – (4.4) прийме вигляд

, (4.2а)

(4.3а)

(4.4а)

Таким чином, шукана функція залежить від трьох величин – x, , a, що мають різну розмірність. В той же час відомо, що фізичні закономірності володіють властивістю інваріантності по відношенню до вибору одиниць вимірювання. Звідси безпосередньо витікає, що розмірні величини x, , a повинні утворити деяку безрозмірну комбінацію. Така комбінація може бути представлена у вигляді відношення , де m – будь-яке число. З практичних міркувань зручно ввести змінну (введення коефіцієнта 1/2 стане ясно з подальшого аналізу ) і шукати розв’язок у вигляді . Перейдемо в рівнянні теплопровідності до нової змінної, використовуючи при цьому відомі правила диференціювання складної функції:

;

;

.

Підставляючи обчислені значення похідних в рівняння (4.2а), одержимо

. (4.5)

Таким чином, за допомогою підстановки нам вдалося перейти від диференціального рівняння в частинних похідних (4.2а) до звичайного диференціального рівняння, граничні умови для якого запишуться в наступному вигляді:

(4.6)

Для розв’язку рівняння (4.5) позначимо , тоді

.

Це рівняння легко інтегрується, в результаті чого

,

де А – постійна. Враховуючи, що і ще раз виконуючи інтеграцію, одержимо

.

.

Використовуючи першу з граничних умов (4.6), визначимо константу В, яка виявляється рівній одиниці. Друга умова приводить до виразу

.

Невласний інтеграл є табличним, його значення відоме і рівне . Отже, . Остаточне шукане поле температур описується рівнянням вигляду

. (4.7)

Інтеграл є функцією  і часто зустрічається в різних задачах математичної фізики з заданою на нескінченності граничною умовою. Він носить спеціальне найменування інтеграла вірогідності Гауса (інтеграл помилок) і позначається

.

Таблиці функції містяться в математичних довідниках. Вид її, а також функції , приведений на рис. 4.3. Зробимо одне важливе зауваження щодо розповсюдження температурного збурення вглиб напівобмеженого масиву. На достатньо великій відстані від поверхні для будь-якого моменту часу завжди можна знайти таку точку, де відхилення температури від початкової величини незначне (припустимо, менше 1%). Величина _*, що відповідає цій точці, складає 1.84. Звідси

,

. (4.8)

Рівняння (4.8) описує рух фронту температурного збурення в напівобмеженому масиві.

Рис. 4.3. Залежність інтеграла ймовірності Гауса і безрозмірної температури від параметра .

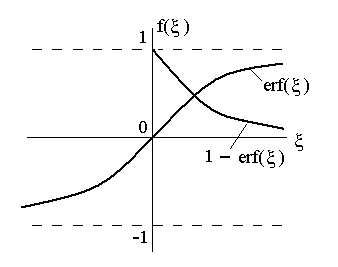Одержаний розподіл температури (4.7) дозволяє розрахувати величину теплового потоку на границі масиву

.

Обчислимо

.

При , і

,

тепловий потік

. (4.9)

Величина носить назву коефіцієнта теплової активності, що характеризує здатність тіла акумулювати (віддавати) тепло.