3.6. Метод Кольрауша.

В

Рис.3.6. Метод Кольрауша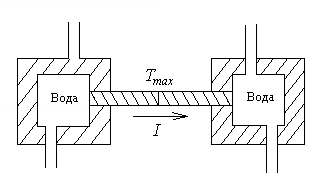

методі Кольрауша коефіцієнт те­плопровідності визначається за те­плотою, що виділяється в металевому стержні при проходженні через нього електричного струму.При чому ство­рені такі умови, що можемо нехту­вати молекулярно-конвективним та радіаційним потоками. При під­триманні на кінцях сержня постійної температури Т₀ спостерігається макси­мальна температура в середині стержня Т_max .

Коєфіцієнт теплопровідності знаходимо з (2.7):

.

Густина джоулевого тепловиді­лення в даному випадку визначаємо, як , де , U – на­пруга, прикладена до кінців дроту,  – пи­тома електропровідність металу, Ом/м; L– довжина дроту, – радіус дроту.

За допомогою наведених формул визначаємо коефіцієнт теплопровідності ме­талевого дроту:

.

Звідси і знаходиться значення коєфіцієнту Відемана-Франца:

,

де – коефіцієнт електропровідності.

Його можна визначити і іншим способом. Знайдемо середню температуру вздовд стержня, як наступний інтеграл:

.

Звідси .

3.7. Визначення коєфіцієнту теплопровідності металів при високих тем­пературах.

Так як для більшості металів та, особливо сплавів, невідома залежність повної випромінювальної здатності матеріалу від температури. Тому стає питання: як врахувати тепловтрати випромінюванням і при цьому не визначати залежність коефіцієнта чорноти від температури.

Розглянемо короткий металевий стержень, довжиною 2ℓ, у якого кінці х=0 і q=2ℓ знаходяться при температурі навколишнього середовища T_g. Почнемо на­грівати цей зразок електричним струмом I до якоїсь температури у вакуумі T(x). Тоді нехтуючи температурною залежністю λ, та ε та не враховуючи граді­єнт температури по радіусу (зразок повинен бути достатньо тоненький), можна отримати наступне рівняння теплового балансу при стаціонарному режимі

, (3.2)

де λ – коефіцієнт теплопровідності, S – площа поперечного перетину, p – пе­риметр стержню, ε – коефіцієнт чорноти, σ – константа Стефана-Больцмана, ρ – питомий електроопір матеріалу стержня. Температурну залежність питомого опору представимо у вигляді: , де T_m – максимальна температура дроту (в середині).

Розглянемо область 0 < х < ℓ з крайовими умовами:

ℓ (3.3)

Проінтегруємо один раз по Т рівняння (3.2). Для цього зробимо наступні пе­ретворення:

, .

В результаті маємо

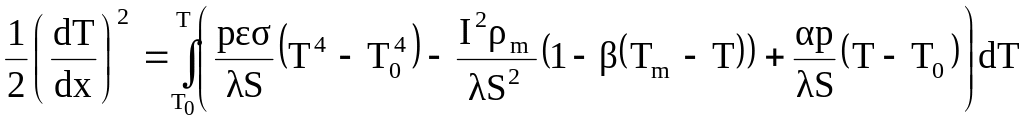
і

.

.

Константу інтегрування знаходимо з граничних умов (3.2), вважаючи що при х = ℓ, температура є максимальною .

Таким чином рівняння теплопровідності зводиться до інтегралу:

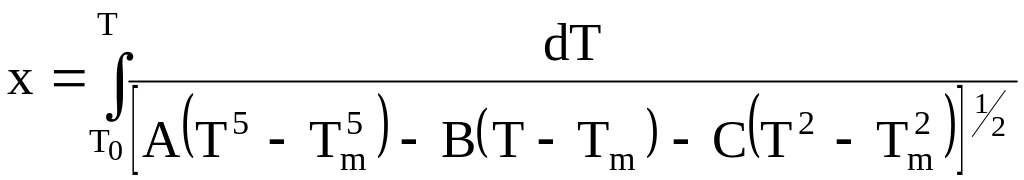, (3.4)

де ; (3.5)

Рівняння (3.4) неможливо прямо проінтегрувати. Тому припустимо, що тем­пература по стержню незначним чином відрізняється від температури в сере­дині стержня. Тоді можна зробити наближено заміни, позначивши різницю темпера­тури відносно температури середини стержня, як :

, .

Тоді рівняння (3.3) перепишеться у вигляді:

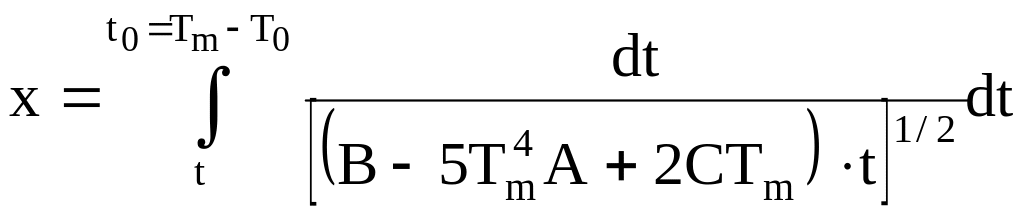
Перейдемо до інших координат  = ℓ – х. Вони більш зручні, адже тепер розподіл температури по  вздовж стержня є симетричним. Тоді попередній інтеграл:

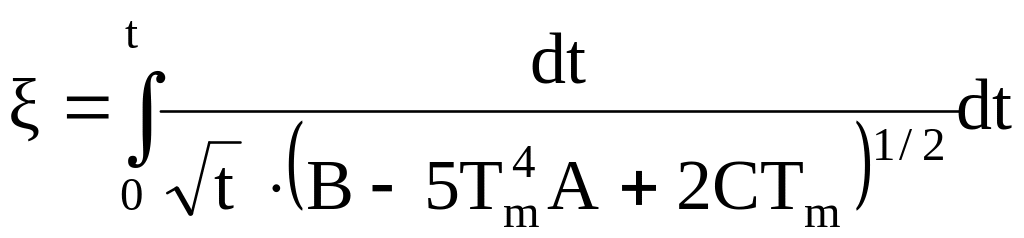і .

З цього рівняння видно, що розподіл температур в околі середини короткого металевого стержня підкоряється параболічному закону, що стверджується експериментально.

Отже , , де

. (3.6)

З формул (3.5) та (3.6) маємо

,

звідки можна визначити коефіцієнт теплопровідності

. (3.7)

Але у правій частині рівняння нам невідомий параметр повної випромінювальної здатності , так як його значення визначається з додаткового експерименту. Для визначення необхідно мати доволі довгі зразки, щоб можна було знехтувати втратами тепла на кінцях в порівнянні з радіацією в навколишнє середовище. Виготовлення довгих зразків не завжди можлива із-за крихкості вивчаючих матеріалів. У зв’язку з цим виникає необхідність у розробці метода визначення теплопровідності на зразках, налаштованих у лабораторній практиці .

Один з шляхів вирішення цієї задачі складається у наступному. Нехай існує два зразки однакового діаметру та хімічного змісту, але з різною довжиною. Припустимо також, що ці зразки нагріваються різним по силі струмом , відповідно I₁ та I₂, до однакової температури середини стержня T_m. Тоді можна вирішити систему рівнянь (3.7) і отримати формули розрахунків для визначення теплопровідності на зразках кінцевої довжини:

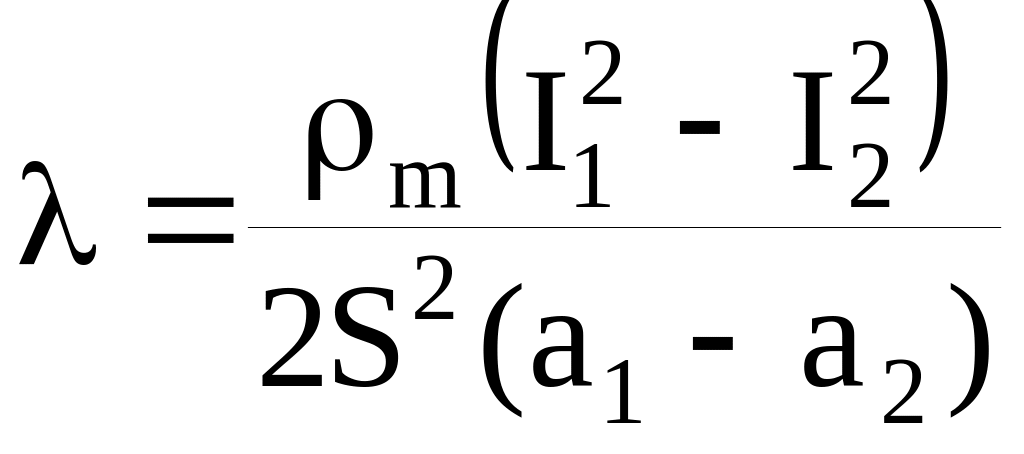. (3.8)

Однак для обчислення необхідно вивчати розподіл температури вздовж стержня, що створює значні експериментальні труднощі і вносить суттєву помилку в кінцевий результат.

Зробимо це наступним чином. Розглянемо ділянку зразка, що примикає до його середини. Координату , як ці раніше, відраховувати від середини. Нехай довжина вибраної ділянки буде 2L. Припустимо спочатку, що цей зразок рівномірно нагрівається до температури Т_m, його загальний опір дорівнює R_m, питомий електроопір ρ_m. Тоді маємо .

Тепер розглянемо ту саму ділянку, але нагріту нерівномірно. У цьому випадку можна записати:

де t = Tm – T(x) << T_m і - температурний коефіцієнт опору в даній області температур. Тоді повний опір стержня

.

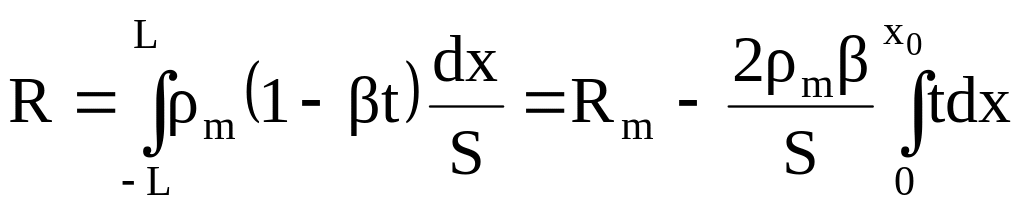У нашому випадку розподіл температури підкоряється параболічному закону. Це дає змогу написати для електричного опору

.

Звідси

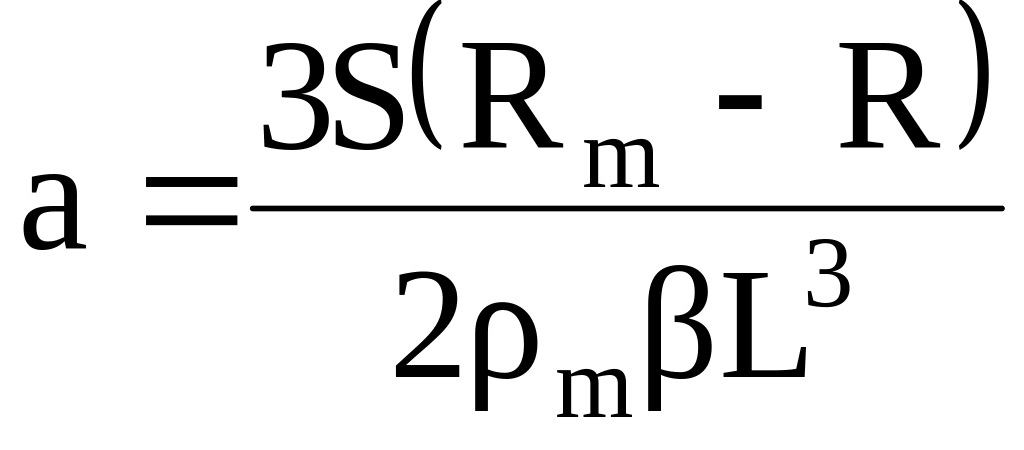. (3.9)

Тут R – опір ділянки довжиною 2L при наявності градієнта температури.

Таким чином, для зразків, у яких питомий опір помітно залежить від температури, можна з достатньою точністю вивчати розподіл температури за допомогою вимірювання опору на певній ділянці довжини.

Як видно з відношення (3.9), для визначення величини необхідно знати опір розглянутої ділянки R_m при відсутності градієнта температури, тобто для зразка у якого втрати тепла на кінцях незначні або, іншою мовою, для нескінченно довгого зразка. Така умова, як відзначалася раніше, неприпустима. У зв’язку з цим для визначення теплопровідності будемо розглядати два зразка з різними довжинами. Як видно, величина λ визначається із співвідношення (3.8).

Отже, необхідно знайти різницю величин

,

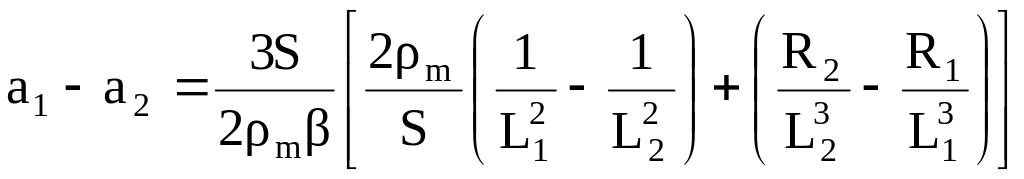де R₁ і R₂ – відповідно опори для першого та другого зразків довжиною 2L₁ і 2L₂. Температура середин цих зразків однакові і дорівнюють Т_m. В результаті маємо для коефіцієнта теплопровідності розрахункову формулу:

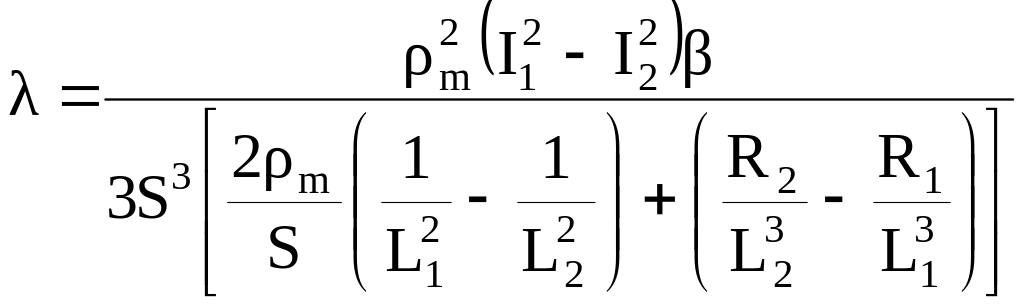
Дана залежність являється розрахунковою для визначення коефіцієнту теплопровідності. Слід відзначити, що зміна вивчення розподілу температури вимірюваннями електричного опору в значній ступені підвищує точність результатів, так як визначення величини опору може здійснюватися з великим ступенем точності у широкому температурному інтервалі.

У випадку, коли брати опір однакових ділянок різних дротиків, формула для визначення коефіцієнту теплопровідності спрощується:

,

де R₁ і R₂ – відповідно опори ділянки довжиною 2L для першого та другого зразків.