10.7. Реализация логических функций
Как отмечалось выше, функции ИЛИ—НЕ и И—НЕ являются универсальными, так как с их помощью можно реализовать любое логическое уравнение. Например, при помощи только элемента И-108 (2ИЛИ—НЕ) можно получить любую логическую функцию. На рис. 10.5, а приведена блок-схема элемента И-108 на два входа х1, х2. Цифровые обозначения 2, 5 являются входами схемы, а 3 — ее выходом. На рис. 10.5, б на элементе И-108 реализована функция «запрета». При отсутст-
Рис. 10.5. Реализация логических функций на элементах И-108
Рис. 10.6. Блок-схемы логических элементов серии И
вии на входе запрета х2 сигнал на выходе у появляется одновременно с х1, при наличии сигнала запрета х2, сигнал на выходе отсутствует.
Реализация функции «Память» на элементе И-108 приведена на рис. 10.5, в. При подаче сигнала на вход х1 (включение памяти) появляется сигнал на прямом выходе 3 и исчезает на инверсном 3'. Это состояние сохраняется до подачи на вход х2 сигнала отключения памяти. Реализация функции ИЛИ производится элементами типа И-105 (рис. 10.5, г). На рис. 10.5, д показан элемент И-106, реализующий функцию ЗИ.
Реализацию функции НЕ можно произвести на одном из входов элемента И-108 (рис. 10.5, е).
Характерной особенностью этих элементов является весьма широкий функциональный набор: например, элемент И-101 представляет собой семь независимых инверторов НЕ в одном блоке (рис. 10.6, а). Входами являются выводы 2, 5, 7, 8, 10,
12, 15. Выходами являются выводы 3, 4, 6, 9, 11, 13, 14. Пита-ние+15 В подается на вывод 1 и —15В на вывод 16 (на блок-схеме отмечены отдельно).
Элемент И-102 (рис. 10.6, б) состоит из двух независимых схем, каждая из которых реализует функцию 4И.
Выводы 4 и 13 являются расширительными.
Базовым элементом этой серии является элемент И-103 (рис. 10.6, в), который состоит из четырех независимых схем, каждая из которых реализует функцию 2И—НЕ. Остальные элементы реализуют следующие функции: И-104 (4И—НЕ); И-105 (4 ИЛИ). И-106 (ЗИ-3 ИЛИ); И-107 (2И-НЕ, НЕ); И-108 (2 ИЛИ—НЕ), И-109 (4И-2 ИЛИ-НЕ).
При помощи этих функциональных наборов можно реализовать любую функцию.
10.8. Реализация математико-логических операций на элементах и-108
Как отмечалось выше, при помощи элемента И-108 серии «Логика-И» можно реализовать (синтезировать) любую логическую функцию.
1. Логическое сложение. Задана функция у = х1+ х2, применяя закон двойной инверсии, ее можно записать как у = х1+ х2= = ¬¬(х1+ х2)· По полученному выражению синтезируется схема
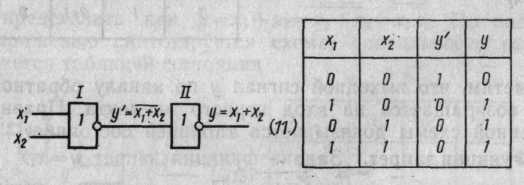
На первом элементе ИЛИ—НЕ (I) производится сложение х1+ х2, и результат на выходе инверсируется первый раз у' = = ¬(х1+ х2). Инверсируя на втором элементе II второй раз этот результат, получаем требуемую выходную функцию у = х1+ х2, что доказывается таблицей состояния.
2. Логическое умножение. Задана функция у = х1 х2, ее
можно записать как y= х1 х2= ¬¬(х1 х2)· Так как мы имеем элемент сложения (ИЛИ), то необходимо функцию преобразовать, т. е.
у =х1 х2 = ¬(х1 х2) = ¬(¬х1+ ¬х2) и по полученному выражению синтезируется схема.
На выходе первых I элементов получены инверсии х1, х2, которые суммируются вторым II элементом и результаты (общая черта) инверсируются. Полученный результат отвечает заданной функции у=х1х2, что доказывается таблицей состояния.
3. Функция память. Задана функция память у = (х1+у)¬х2, преобразуем ее
По полученному выражению синтезируется схема
Заметим, что выходной сигнал у по каналу обратной связи (ОС) возвращается на вход первого элемента. Правильность полученной схемы доказывается таблицей состояния.
4. Функция запрет. Задана функция запрет y=х1¬х2 . Преоб-
разуем ее
По полученному выражению синтезируется схема
Правильность полученной схемы доказывается таблицей состояния.