Глава 6 элементы и узлы цифровой автоматики

6.1. ФИЗИЧЕСКИЕ СИГНАЛЫ ПРЕДСТАВЛЕНИЯ ИНФОРМАЦИИ В ЦИФРОВОЙ АВТОМАТИКЕ, ДВОИЧНЫЕ ЧИСЛА

Физические сигналы. В цифровой автоматике информация представляется ρ основном в двоичном алфавите (0,1). Физическими аналогами знаков 0 и 1 служат сигналы, способные принимать два хорошо различимых значения, в частности отсутствие и наличие электрического импульса. При этом переменные и соответствующие им импульсные сигналы изменяются не непрерывно, а лишь в дискретные моменты времени, обозначаемые целыми неотрицательными числами: 0, 1, 2, 3,..., i,... Временной интервал между двумя соседними моментами дискретного времени называется тактом. Цифровые устройства часто имеют генератор синхронизирующих сигналов (СС), отмечающих такты в виде моментов дискретного времени.

При импульсном представлении информации (рис. 6.1) единичное и нулевое значение двоичной информации отображается наличием или отсутствием электрического импульса.

Импульсный сигнал можно характеризовать амплитудой U_m, продолжительностью импульса по основанию t_ОСН, длительностью фронта t_фр и среза t_cp.

Многоразрядные двоичные числа (слова) могут быть представлены последовательным или параллельным кодом.

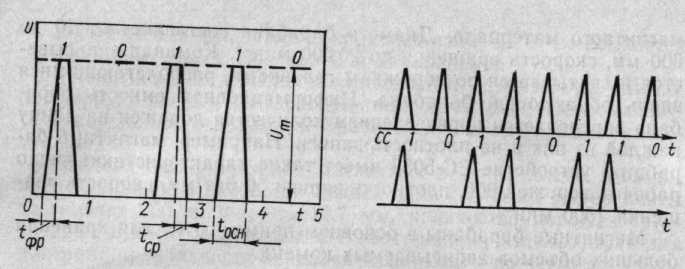
Рис. 6.1 Импульсное представление двоичной информации

Рис. 6.2. Последовательный импульсный код Рис. 6.3. Параллельный импульсный код

При последовательном коде каждый временной такт предназначен для отображения одного разряда кода слова (рис. 6.2). В этом случае все разряды слова фиксируются по очереди одним и тем же элементом и проходят через одну линию передачи информации.

При параллельном коде все разряды двоичного кода слова представляются в одном временном такте, фиксируются отдельными элементами и проходят через отдельные линии, каждая из которых служит для представления и передачи только одного разряда слова.

При параллельной передаче информации код слова развертывается не во времени, а в пространстве, так как значения всех разрядов слова передаются по нескольким линиям одновременно (рис. 6.3).

При использовании последовательного кода передача слов из одного узла в другой производится поочередно для каждого разряда слова, поэтому последовательные устройства работают медленнее, чем параллельные. Но последние требуют большего объема аппаратуры.

Двоичная система представления чисел и двоичная арифметика. Любое число x может быть записано в виде уравнения

x=a_m2^m+a_m-12^m-1+...+a₁2¹+a₀2⁰+a_-12^-1+

+а_-22^-2+ . . . , (6.1)

где a_i — коэффициенты, которые имеют значение 0 либо 1.

Эта формула дает выражение двоичного кода любого числа, например, число 173,626= 1 ·2⁷ + 0·2⁶ + 1 ·2⁵ + 0· 2⁴ + 1·2³ + + 1·2² + 0·2¹ + 1·2⁰+1·2^-1 + 0·2^-2+1·2^-3. Следовательно, двоичный код числа 173,626 имеет значение |0|0||0|, |0|.

Двоичные коды в цифровой автоматике весьма удобны, так как каждый разряд двоичного числа фиксируется простейшим элементом, имеющим два устойчивых состояния, в частности

триггером.

Кроме того, двоичная арифметика является наиболее простой, в чем мы ниже убедимся.

Правила выполнения арифметических действий над двоичными числами задаются таблицами двоичного сложения, вычитания, умножения.

Двоичное сложение:	Двоичное вычитание:	Двоичное умножение:
0+0=0	0—0=0	0×0=0
0+1=1	1—0=1	0×1=0
1+0=1	1—1=0	1×0=0
1+1=10	10—1=1	1×1=1

При сложении в каждом разряде производится сложение двух цифр слагаемых или этих цифр и единицы, если имеется перенос из соседнего младшего разряда. В результате получается цифра соответствующего разряда суммы и, возможно, также единица переноса в старший разряд.

Пример сложения двух десятичных и соответствующих им двоичных чисел:

При вычитании двоичных чисел в данном разряде при необходимости занимается 1 из следующего старшего разряда. Эта занимаемая 1 равна двум 1 данного разряда. Заем производится каждый раз, когда цифра в разряде вычитаемого больше цифры в том же разряде уменьшаемого.

Пример

Умножение двоичных многоразрядных чисел производится путем образования частичных произведений и последующего их суммирования. Каждое частичное произведение равно 0, если в соответствующем разряде множителя стоит 0, или равно

множимому, сдвинутому на соответствующее число разрядов влево, если в разряде множителя стоит 1. Следовательно, операция умножения многоразрядных двоичных чисел сводится к операциям сдвига и сложения.

Пример 1011,1×101,01 = 111100,011

Положение запятой определяется так же, как при умножении десятичных чисел.

Особенности выполнения деления двоичных чисел поясняется примером:

1100,011:10,01 = ?

Благодаря простоте правил двоичной арифметики применение двоичной системы представления чисел требует простых устройств цифровой автоматики.