63.Математичне сподівання та дисперсія випадкової величини, розподіленої за біномним законом.

D(ϻ)= D(ϻ₁+ϻ₂+…+ϻ_n)= D(ϻ₁)+D(ϻ₂)+..+D(ϻ_n)=npq.

E(x)=np.

64. Формула для дисперсії випадкової величини(ряд).

D(X)= _k=1∑^∞(x_k-E(X))² p_k.

65. Формула для дисперсії неперервної випадкової величини (інтеграл).

D(X)= _-∞∫^∞(x-E(X))²p(x)dx.

66. Означення коваріації випадкових величин. Коваріація випадкових величин Х та Y характеризує відхилення випадкового вектора х,у від точки з координатами (E(x),E(y)).

67.Означення коефіцієнта кореляції. Коефіцієнтом кореляції між випадковими величинами Х та Y називається відношення коваріації до добутку середніх квадратичних відхилень цих величин. 68. |ρ(X,Y)|=1, тоді і лише тоді, коли випадкові величини зв’язані лінійною залежністю Y=αX+β. Тоді:

P(X,Y)={1, якщо α>1;

{-1, якщо α<1.

69. Формули для α , β у рівнянні прямої регресії Y на X. ;

.

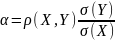70. Суть закону великих чисел. Полягає в тому, що в разі дуже великої кількості випадкових явищ усереднений їхній результат практично перестає бути випадковим і може бути передбачений із великю часткою вірогідності.

71. Теорема Маркова (закон великих чисел) Якщо випадкові величини Х₁, Х₂,…, Х_n ,… попарно незалежні, мають скінченні математичні сподівання і для їхніх дисперсій виконується рівність 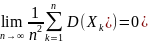, то для будь-якого числа ε > 0 виконується граничне співвідношення , яке означає, що послідовність середніх арифметичних цих випадкових величин збігається за ймовірністю до середнього арифметичного їхніх математичних сподівань.

72. Теорема Чебишова (закон великих чисел)

Якщо випадкові величини X₁, X₂,…, X_n… попарно незалежні, мають скінченні математичні сподівання та обмежені в сукупності дисперсії D(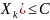 , K=1,2…, де C=const >0, то для будь-якого числа виконується граничне співвідношення

.

73. Суть центральної граничної теореми. Центральна гранична теорема встановлює умови, за яких розподіл суми випадкових величин наближається до нормального закону.

74. Теорема Глівенка. Для будь-якого дійсного числа х за необмеженого зростання обсягу вибірки n емпірична функція розподілу F_n(x) збігається за імовірністю до теоретичної функції розподілу F(x) тобто: будь–яке ε>0 і будь-який х є R; lim_n→∞P{|Fn(x)- F(x)|<ε}=1.

75. Умова слушності незміщеної оцінки. Якщо дисперсія незміщеної оцінки при необмеженому зростанні обсягу вибірки прямує до нуля, то така оцінка є слушною, тобто:

E(Ɵ*_n)=Ɵ ˅ n, lim_n→∞D(Ɵ*_n)=0 => ˅ ε>0 , lim_n→∞P(|Ɵ*_n-Ɵ|<ε}=1.

76.Незміщена і слушна оцінка математичного сподівання це…вибіркове середнє

a*_n=xˉ=1/n ∑_i=1 ⁿ x_i.

77. Точкова оцінка дисперсії – це…Якщо випадкова вибірка складається з результатів n незалежних випробувань х1,х2,..,хn над випадковою величиною Х із математичним сподіванням Е(х)=а і дисперсією D(x)= σ², то за точкову оцінку дисперсії беруть вибіркову дисперсію D_B=1/n∑_k=1 ⁿ(x_k -xˉ)², яка є зміщеною оцінкою параметра D(x)= σ².

78. Незміщена точкова оцінка дисперсії це–… підправлена вибіркова дисперсія: S2=1/n-1 ∑_x=1 ⁿ(x_k -xˉ)²

79. Означення інтервальної оцінки параметра розподілу. Інтервальною оцінкою називається інтервал (Ɵ*-δ, Ɵ*+δ), для якого виконується: P{|Ɵ-Ɵ*|<δ}= ϒ.

80. Дві теореми про надійні межі для математичного сподівання у випадку відомого середнього квадратичного відхилення Теорема 1: Нехай Х нормально розподілена ознака генеральної сукупності, для якої Е(Х)=а, D(X)= . 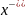- вибіркове середнє обчислюємо за вибіркою обсягу n з цієї генеральної сукупності. Тоді для випливає P . Теорема2: Нехай Х довільно розподілена ознака генеральної сукупності, для якої Е(Х)=а, D(X)= . - вибіркове середнє обчислюємо за вибіркою обсягу n з цієї генеральної сукупності. Тоді для випливає .

81. Інтервали довіри для математичного сподівання у випадку відомого середнього квадратичного відхилення Нехай x₁ , x₂,…,x_n– результати n незалежних спостережень за випадковою величиною Х, на підставі яких необхідно знайти інтервал довіри для невідомого параметра a = E(X ). Оскільки для математичного сподівання точковою оцінкою є вибіркове середнє x , то для знаходження інтервалу довіри x −δ < a < x +δ потрібно розв’язати рівняння: P{| x − a |<δ } = ⇔ P{x −δ < a < x +δ}= Якщо середнє квадратичне відхилення σ випадкової величини Х відоме, то розв’язок рівняння можна знайти, використовуючи рівності P і . Так, якщо σ відоме, Х – нормально розподілена випадкова величина або обсяг вибірки значний ( n > 30 ), то ми можемо записати, що P . Тоді, якщо t tγ = − розв’язок рівняння 2Φ(t) =γ , то з надійністю γ інтервал є інтервалом довіри для математичного сподівання a.

82. Інтервали довіри для математичного сподівання у випадку невідомого середнього квадратичного відхилення Якщо середнє квадратичне відхилення σ невідоме, але обсяг вибірки значний ( n > 30 ), то інтервал довіри можна записати у вигляді , де s − підправлене середнє квадратичне відхилення, знайдене за вибіркою обсягу n. Якщо середнє квадратичне відхилення σ невідоме, обсяг вибірки незначний ( n < 30 ), але Х – нормально розподілена випадкова величина, то інтервал довіри також записують у вигляді

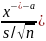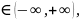, де значення t _γ = t (γ,n) шукають за таблицями як розв’язок рівняння P , де T= −випадкова величина, розподілена за законом Ст’юдента з k = n −1 ступенями вільності, який характеризується щільністю розподілу s(x, n)= x де n B – деяка нормуюча константа. Розподіл Ст’юдента залежить лише від одного параметра n і при n → ∞ наближається до нормального закону розподілу.