1.Формула для кількості перестановок з повтореннями. ( , ,…, ) =

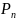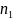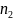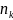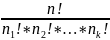
2.Теорема додавання ймовірностей.

∀ A, B P(A + B) = P(A) + P(B) − P(AB) 3. Означення несумісних подій і теорема додавання для них. Події А і В називаються несумісними, якщо їх добуток є неможливою подією, тобто А * В = порожня множина.

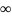
U від і=1 до 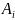= 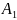+ + 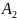+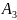… відбувається тоді, коли відбувається хоча б одна з подій , , ,…

4. Класичне означення ймовірності. ймовірністю події А називається відношення кількості сприятливих для події А елементарних подій до кількості всіх рівноможливих і попарно несумісних результатів випробування.

5. Означення геометричної ймовірності.

Геометричною ймовірністю події А називають відношення міри до міри 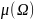, тобто

P(A) =

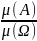
6.Умовна ймовірність (формула).

P(A/B) =

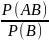
7. Теорема множення ймовірностей.

якщо P(A) > 0, P(B) > 0, то P(AB) = P(A)P(B/ A) = P(B)P(A/ B)

8. Теорема множення ймовірностей для незалежних подій.

P(AB) = P(A) * P(B)

9. Формула повної ймовірності та формули Байеса.

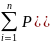P(A) = ) P(A/ )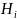

P( /A)= P( ) P(A/ ) поділити на ) P(A/ )

10. Біномна формула та пояснення до неї.

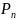(k) =

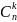
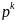
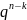
Вона виражає ймовірність того, що кількість успіхів в серії з п послідовних

незалежних випробувань за схемою Бернуллі дорівнює k.

11. Функція Лапласа (формула).

Ф(x) =

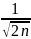
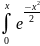
12. Φ(x)− функція Лапласа. Φ(0) =0 ; Φ(−∞) = -0,5 ; Φ(∞) = 0,5 13. Означення функції розподілу ймовірностей випадкової величини. Функція дійсної змінної х, x∈R = (−∞,+ ∞), визначена рівністю F(x) = P{ω : X (ω) < x} = P{X < x}, називається функцією розподілу випадкової величини X = X (ω) 14. Означення дискретної випадкової величини. Випадкова величина називається дискретною , якщо множина її можливих значень є скінченною або зліченною.

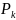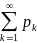15. Якщо X − дискретна випадкова величина і = P{X= }, то = 1

16. Формула для функції розподілу ймовірностей неперервної випадкової величини.

F(x) = P{X<x} =

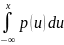
17.X − довільна випадкова величина, P{a ≤X <b} = F(b) – F(a) =

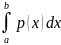
18. X − неперервна випадкова величина, P{a ≤X <b} = P{a <X <b} =

19. p(x) − щільність розподілу ймовірностей, = = = 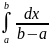1

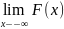20.F(x) – функція розподілу, = 1 , = 0

21. Означення математичного сподівання дискретної випадкової величини. Математичним сподіванням дискретної випадкової величини Х називається число E(X) = 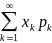= 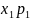+ + 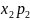….., якщо ряд у правій частині абсолютно збіжний.

22. Означення математичного сподівання неперервної випадкової величини.

Математичним сподіванням неперервної випадкової величини Х називається число

E(X) = , якщо інтеграл у правій частині абсолютно збіжний.

23. Означення дисперсії випадкової величини.

Дисперсією випадкової величини Х називається математичне сподівання квадрата відхилення цієї випадкової величини від її математичного сподівання, тобто

D(X) = E( X - E(X) ) в квадраті.

24. Математичне сподівання та дисперсія випадкової величини, розподіленої за законом Пуассона.

D(X ) = λ, E(X) = λ.

25. Математичне сподівання рівномірно розподіленої випадкової величини.

E(X) = `

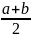26. X − неперервна випадкова величина, E( f (X )) =

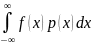
27. X − дискретна випадкова величина, E( f (X )) = ) 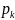28. Якщо випадкові величини Х і Y – незалежні, то E(XY) = E(X) * E(Y), D(X +Y) = D(X) + D(Y) , ρ(X,Y) = =0 29. Математичне сподівання та дисперсія нормально розподіленої випадкової величини.

E(X)=a, D(X) =

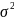
30. Нерівність Чебишова (перша форма).

Якщо X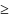 0, то P{X 1} 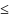E(X)

31. Нерівність Чебишова (друга форма).

Якщо випадкова величина Х має скінченні математичне сподівання E(X ) та дисперсію D(X ), то для будь-якого числа ε > 0 виконується нерівність P{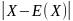 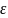} 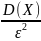33. Початкові та центральні моменти випадкової величини.

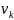= E( ), =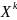

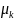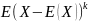
34. Означення емпіричної функції розподілу.

Емпіричною функцією розподілу випадкової величини X називають функцію 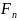(x) , що визначає для будь-якого дійсного числа х відносну частоту подій {X<x}, тобто (x) =

35. Означення незміщеної точкової оцінки параметра розподілу.

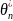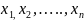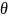Точкова оцінка = ( ) параметра розподілу випадкової величини X називається незміщеною, якщо її математичне сподівання дорівнює точному значенню цього параметра.

36. Означення слушної точкової оцінки параметра розподілу.

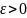
Точкова оцінка = ( ) параметра розподілу називається слушною, якщо збігається за ймовірністю до оцінюваного параметра при необженому зростанні обсягу вибірки, тобто виконується така рівність 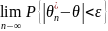= 1

37. Означення ефективної точкової оцінки параметра розподілу.

Незміщенна оцінка = ( ) називається ефективною, якщо вона має найменшу дисперсію серед усіх незміщених оцінок параметра . Обчислених за вибірками одного і того ж обсягу.