34 Вопрос Степенные ряды. Теорема Абеля Теорема об области сходимости степенного ряда.
Степенные ряды.
Основные понятия.
ряд по степеням
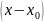
- коэффициент ряда
- цент сходимости, центр разложения.
Х=
-
точка сходимости степенного ряда, если
числовой ряд
сходится.
Совокупность всех точек сходимости степенного ряда называется областью остаточной сходимости.
Теорема Абеля.
Если
степенной ряд
сходится при х=
,
то он абсолютно сходится при любом x
удовлетворяющем неравенство
<
.
Следствие.
Если степенной ряд
расходится при х=
,
то он расходится при любом х
>
.
Теорема об области сходимости степенного ряда.
для этого ряда существует число R- радиус сходимости и интервал: <R. На этом интервале ряд сходится абсолютно, вне интервала ряд расходится в граничных точках х=±R требуется дополнительное исследование.
R= -0-интервальное выражение в точке 0 -Конечной величиной(собственного числа) -Бесконечной величиной (несобственного числа) -вся числовая ось является областью сходимости.
Свойства степенных рядов.
В интервале сходимости сумма степенного ряда является непрерывной функцией переменной х.
<R
x->
2.В интервале сходимости степенной ряд можно почленно дифференцировать произвольное число раз, при этом ряды для производного или исходного ряда имеет одинаковый интервал сходимости(интервал сходимости не меняется).
=S(x).
3.В интервале сходимости степенной ряд можно почленно интегрировать.
=S(x).
4.Арифметические свойства степенных рядов.
абсолютно сходится
на интервале(
-
,
+
)
-//-//-(
-
,
+
),
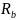то на пересечении интервалов сходимости,
степенные ряды можно складывать,
вычитать, перемножать и делить подобно
многочленам при отличие от нуля. Новые
ряды также сходятся.
35 Вопрос. Ряды Тейлора и Маклорена. Теорема о единственности разложения. Теорема о необходимых и достаточных условиях разложимости; теорема о достаточных условиях разложимости функции в ряд Тейлора.
Ряды Тейлора
Степенной
ряд
называется рядом Тейлора , для функции
f(x)
на (
-
,
+
),
если в каждой точке этого интервала
ряд сходится абсолютно и его сумма =
f(x)=
Теорема Тейлора
Если функция разлагается в ряд Тейлора на некотором интервале , то коэффициент разложения вычисляется по формулам:
=
n=0,1,2…..
=
=
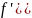=f
=
=
f
Теорема о необходимых и достаточных условиях разложимости.
Чтобы функция f(x) разлагалась в ряд Тейлора по степеням двучлена на <R необходимо и достаточно:
1.Чтобы в каждой точке этого интервала существует непрерывная производственная функция n=0,1,2
2.Остаточный
член Тейлора
=0
имея предел, где
=
Q(0;1)
Ряды Маклорена.
=0
n=0,1,2….
36
вопрос
Разложение в ряды Маклорена
основных элементарных функций (
,
cosx,
sinx,
1/(1+x),
ln(1+x),
+…..+
+…,
<
Sinx=x-
+….+
+….
Cosx=1-
+….+(
+…..
38 Вопрос. Комплексные ряды. Сходящиеся абсолютно сходящиеся и условно сходящиеся ряды. Формулы Эйлера.
) – комплексный ряд (1)
i-мнимая единица
Называется сходящимся, если и составлен из действительных и мнимых частей заданного ряда.
Называется абсолютно сходящимся , если
сходятся
Z=x+iy
=
Называется условно сходящимся, если он сходится, а ряд модулей расходится
Все свойства абсолютно сходящихся рядов действительной области переносятся на комплексные ряды, абсолютно сходящиеся в комплексной области.
Формулы Эйлера:
,
Где e — основание натурального логарифма,
i— мнимая единица.
,
