3)Орнына қоямыз.

2.Ықтималдықтар теориясы. Негізгі ұғымдар..

Ықтималдылық теориясының негізі-тәжірбие, сынақ, бақылау. Ең жиі кезд ж\е қарапайым тәжірб\р-теңге лақтыру, нысанаға оқ ату, қораптан шар суыру. Ықтималдылықтың негізгі ұғымд\ы-оқиғалар ж\е олардың п.б. ықт\ы. Оқиға д\з-белгілі бір себептерден туатын ж\е орындалатын құбылыс. 1. Ақиқат-міндетті түрде сынақ нәтижесәнде п.б. оқиға. 2.мүмкін емес-сынақ нәтижесінде п.б. мүмкіндігі жоқ оқиға. 3.кездейсоқ-сынақ нәт\е п.б. да п.болмауы дамүмкін оқиға. Ықтималдықтың классикалық анықтамасы Жалғыз ж\е тең мүмкіндікті үйлесімсіз оқиғалардың ішінен А оқиғасының орындалу ықт\ы P(A)=m\n

Емтихан билеті №8

1.Бірінші ретті біртекті және біртекті емес сызықтық дифференциалдық теңдеулер.

2.Ықтималдықтарды қосу және көбейту формулалары. А мен Б ның көб\і деп олардың бірге п.б тұратын оұиғаны айт. А мен Б ның үйлесімді қосынд\ы деп кемінде біреуінің п.б тұратын оқиға.

Емтихан билеті №7

1.Бірінші ретті біртекті дифференциалдық теңдеулер.

2.Қос интегралдың механикада қолданылуы. Oxy жазықтығында аумағы Dоблысы , ал тығыздығы γ=γ(x,y) болатын пластинаның массасы :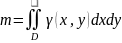 Ох жəне Оу осьтеріне қарағандағы статикалық моменттері формулаларымен анықталады . Пластинаның ауырлық центрінің координаттары 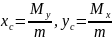формулаларымен

анықталады . Ох , Оу осьтеріне жəне координата бас нүктесіне қарағандағы инерция моменттері

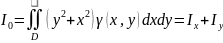формулаларымен анықталады .

Емтихан билеті №6

1.Айнымалылары ажыратылған және ажыратылатын дифференциалдық теңдеулер.

2.Қос интегралдың геометрияда қолданылуы.

3.Екi мергеннiң әрқайсысы атқан кезде дәл тигізу ықтималдылығы: Р₁=0,9, Р₂=0,7. Нысанаға екеуi бір-бірден оқ атқанда тек біреуінің дәл тигiзу ықтималдылығы қандай?

Емтихан билеті №5

1.Бірінші ретті дифференциалдық теңдеулер. Анықтамасы, реті. Жалпы және дара шешімдері.

2.Үштік интегралда айнымалыны алмастыру. Декарттық координаталардан цилиндрлік координаталарға көшу. Үштік интегралда x,y,z координаталарынан x=x(u,v,w), y=y(u,v,w), z=z(u,v,w) формулаларының көмегімен u,v,w координатасына көшу формуласымен жүзеге асады , мұндағы J= -якобиан

x=x(u,v,w), y=y(u,v,w), z=z(u,v,w)-үш өлшемді V аймағында үзіліссіз , əрі үзіліссіз бірінші ретті дербес туындылары бар функциялар . Дербес жағдайда x,y,z тікбұрышты координаттардан

) формулаларының көмегімен цилиндрлік координаттарға көшкенде якобиан J=r болады

Емтихан билеті №4

1.Көп айнымалылы функциялардың экстремумы. D облысында анықталған z=f(x.y) функциясы берілсін. Осы облыста жататын 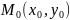нүктесінің маңайындағы барлық M(x,y) нүктелерінде теңсіздігі орындалса, z=f(x.y) онда функциясы 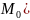нүктесінде максимум ( минимум ) мəнін қабылдайды . " Максимум " жəне " минимум " мəндері экстремум мəндері деп аталады. Қажетті және жеткілікті шарттары.

2.Қос интегралда айнымалыны алмастыру. Қос интегралда x,y координаталарынан x=x(u,v,), y=y(u,v), z=z(u,v) формулаларының көмегімен u,v, координатасына көшу 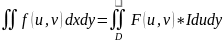формуласымен жүзеге асады , мұндағы 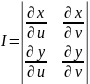якобиан. x=x(u,v), y=y(u,v) өзара бірмәнді, D облысында үзіліссіз , əрі үзіліссіз бірінші ретті дербес туындылары бар функциялар

Декарттық координаталардан полярлық координаталарға көшу.Қос интегралда тік бұрышты x,y координаттарынан 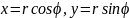формулаларының көмегімен ϕ ,r полярлық

координаталарына көшу 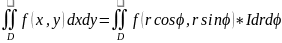формуласымен жүзеге асады . Мұндағы 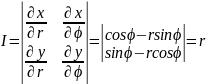болады. Егер интегралдау D облысы 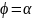ж\е 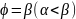сəулелерімен, 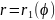ж\е 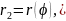жатқанда 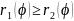болса қисық сызықтармен шектелсе , онда қос интеграл формуласымен есептелінеді

Емтихан билеті №3