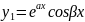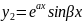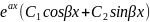- •2.Геометриялық (прогрессия) және жалпы гармоникалық қатарлар жинақтылығы.
- •1.Қатарлар. Оң таңбалы сандық қатарлардың жинақтылық белгілері.
- •2.Көп айнымалылы күрделі функцияның туындысы.
- •2.Дәрежелік қатарлар. Дәрежелік қатардың жинақтылық радиусы және интервалы.
- •1.Оң таңбалы сандық қатарлардың жинақтылық белгілері.
- •2.Бірінші ретті біртектіге келтірілетін дифференциалдық теңдеулер.
- •2.Бірінші ретті біртектіге келтірілетін дифференциалдық теңдеулер.
- •3)Орнына қоямыз.
- •2.Ықтималдықтар теориясы. Негізгі ұғымдар..
- •1.Бірінші ретті біртекті және біртекті емес сызықтық дифференциалдық теңдеулер.
- •1.Бірінші ретті біртекті дифференциалдық теңдеулер.
- •1.Айнымалылары ажыратылған және ажыратылатын дифференциалдық теңдеулер.
- •1.Бірінші ретті дифференциалдық теңдеулер. Анықтамасы, реті. Жалпы және дара шешімдері.
- •1.Көп айнымалылы функцияның дербес туындылары. Жоғарғы ретті дербес туындылар.
- •2.Қос интегралдар. Қасиеттері. Декарттық координаталарда есептелінуі.
- •2.Комбинаторика формулаларын қолданып ықтималдықты есептеу.
Емтихан билеті №25
1.Бірінші
ретті толық дифференциалды теңдеулер.
Егер P(x;y)dx+Q(x;y)dy=0 теңдеуі
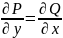 шартын
қанағаттандырса , яғни теңдеудің сол
жағы қайсыбір u (x;y) функциясының
дифференциалы болса , онда ол толық
дифференциалды теңдеу деп
аталады .
шартын
қанағаттандырса , яғни теңдеудің сол
жағы қайсыбір u (x;y) функциясының
дифференциалы болса , онда ол толық
дифференциалды теңдеу деп
аталады .
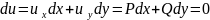
1)
u`x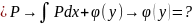
2)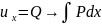
3)орнына қоямыз.
2.Толық
ықтималдық формуласы.
Егер А оқиғасы , өзара үйлесімсіз толық
топ құратын
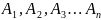 оқиғасының
біреуімен бірге н\е біреуінен кейін
п.б. онда А оқиғасы келесі формуламен
анықталады:
оқиғасының
біреуімен бірге н\е біреуінен кейін
п.б. онда А оқиғасы келесі формуламен
анықталады:
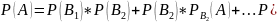 )*
)*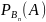 Мұндағы
Мұндағы
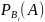 шартты ықт\р.
шартты ықт\р.
Бейес
формуласы. Жоғарыдағы
шарттар орындалғанда Бейес ф\ы орынд.
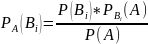 Бұл ф\а оқиға ықтималдылығының А оқиғасы
п.б. кейін есептеуде қолд.
Бұл ф\а оқиға ықтималдылығының А оқиғасы
п.б. кейін есептеуде қолд.
Емтихан билеті №24
1.Тұрақты
коэффициентті екінші ретті оң жағы
арнайы түрде болатын сызықтық
дифференциалдық теңдеулер.
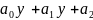 y=0түріндегі теңдеу II ретті коэффициенттері
тұрақты біртекті сызықты теңдеу деп
аталады .
y=0түріндегі теңдеу II ретті коэффициенттері
тұрақты біртекті сызықты теңдеу деп
аталады .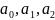 коэффициенттері тұрақты дифференциалдық
теңдеудің шешімін табу үшін алдымен .
коэффициенттері тұрақты дифференциалдық
теңдеудің шешімін табу үшін алдымен .
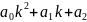 =0 сипаттамалық ( квадраттық болады )
теңдеуін шешу керек .
=0 сипаттамалық ( квадраттық болады )
теңдеуін шешу керек .
Квадрат теңд\ң түбірлері |
Дара шешімі |
Жалпы шешім |
|
|
|
|
|
|
|
|
|
2.Функциялық
қатарлар.
Анықталу облысы ортақ функ\р тізбегі
берілсін
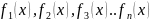
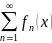 шексіз
қосындысы функциялық
қатарлар
д.а.
Жинақталу облысы.
Функц\қ қатар жинақты болатын аргумент
х тің мәндер жиыны осы қатардың жинақталу
облысы д.а.
шексіз
қосындысы функциялық
қатарлар
д.а.
Жинақталу облысы.
Функц\қ қатар жинақты болатын аргумент
х тің мәндер жиыны осы қатардың жинақталу
облысы д.а.
Емтихан билеті №23
1.Дифференциалдық теңдеулер. Айнымалылары ажыратылған және ажыратылатын теңдеулер.Тəуелсіз айнымалы, ізделінді функция жəне оның туындыларын байланыстыратын теңдеу дифференциалдық теңдеу деп аталады . Егер ізделінді функция тек бір ғана айнымалыдан тəуелді болса , онда дифференциалдық теңдеу қарапайым деп аталады . Біз тек қарапайым дифференциалдық теңдеулерді қарастырамыз. Теңдеудің құрамындағы ең жоғарғы туындының реті дифференциалдық теңдеудің реті деп аталады. Дифференциалдық теңдеудің шешімі немесе интегралы деп теңдеуге қойғанда оны тура теңдікке айналдыратын кез келген f(xy) функциясын айтады . Дифференциалдық теңдеудің шешімін анықтау дифференциалдық теңдеуді интегралдау делінеді . Егер дифференциалдық теңдеудің шешімі , саны теңдеудің ретіне сəйкес келетін тəуелсіз кез келген тұрақтылардан тұрса , онда ол берілген теңдеудің жалпы шешімі деп аталады.
2.Геометриялық (прогрессия) және жалпы гармоникалық қатарлар жинақтылығы.
Емтихан билеті №22
1.Дифференциалдық теңдеулер. Анықтамасы, реті. Шешімдері. Коши есебі. Тəуелсіз айнымалы , ізделінді функция жəне оның туындыларын байланыстыратын теңдеу дифференциалдық теңдеу деп аталады . Егер ізделінді функция тек бір ғана айнымалыдан тəуелді болса , онда дифференциалдық теңдеу қарапайым деп аталады . Біз тек қарапайым дифференциалдық теңдеулерді қарастырамыз. Теңдеудің құрамындағы ең жоғарғы туындының реті дифференциалдық теңдеудің реті деп аталады. Дифференциалдық теңдеудің шешімі немесе интегралы деп теңдеуге қойғанда оны тура теңдікке айналдыратын кез келген f(xy) функциясын айтады . Дифференциалдық теңдеудің шешімін анықтау дифференциалдық теңдеуді интегралдау делінеді . Егер дифференциалдық теңдеудің шешімі , саны теңдеудің ретіне сəйкес келетін тəуелсіз кез келген тұрақтылардан тұрса , онда ол берілген теңдеудің жалпы шешімі деп аталады.
Мысалы - n-ші ретті дифференциалдық теңдеудің
шешімі . Мұндағы
- n-ші ретті дифференциалдық теңдеудің
шешімі . Мұндағы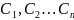 тұрақтыларының орнына мəндер қойып
дара шешімдер алуға болады . n-ші ретті
дифференциалдық теңдеудің
тұрақтыларының орнына мəндер қойып
дара шешімдер алуға болады . n-ші ретті
дифференциалдық теңдеудің
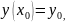
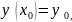
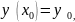
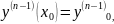 -
бастапқы деп аталатын шарттарды
қанағаттандыратын дара шешімін табу
Коши
есебі
деп аталады .
-
бастапқы деп аталатын шарттарды
қанағаттандыратын дара шешімін табу
Коши
есебі
деп аталады .
2.Үштік
интегралда айнымалыны алмастыру.
Декарттық координаталардан цилиндрлік.
Үштік интегралда x,y,z координаталарынан
x=x(u,v,w),
y=y(u,v,w), z=z(u,v,w) формулаларының
көмегімен u,v,w координатасына көшу
 формуласымен
жүзеге асады , мұндағы
формуласымен
жүзеге асады , мұндағы
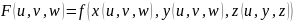 J=
J=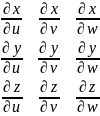 -якобиан
-якобиан
x=x(u,v,w),
y=y(u,v,w), z=z(u,v,w)-үш
өлшемді V аймағында үзіліссіз , əрі
үзіліссіз бірінші ретті дербес туындылары
бар функциялар . Дербес жағдайда x,y,z
тікбұрышты
координаттардан
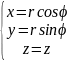
 )
формулаларының
көмегімен
)
формулаларының
көмегімен
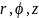 цилиндрлік
координаттарға көшкенде якобиан J=r
болады
цилиндрлік
координаттарға көшкенде якобиан J=r
болады
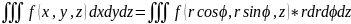
Емтихан билеті №21
1.Қатарлар. Оң таңбалы сандық қатарлардың жинақтылық белгілері.
2.Көп айнымалылы күрделі функцияның туындысы.

Айқын емес функцияның туындысы.
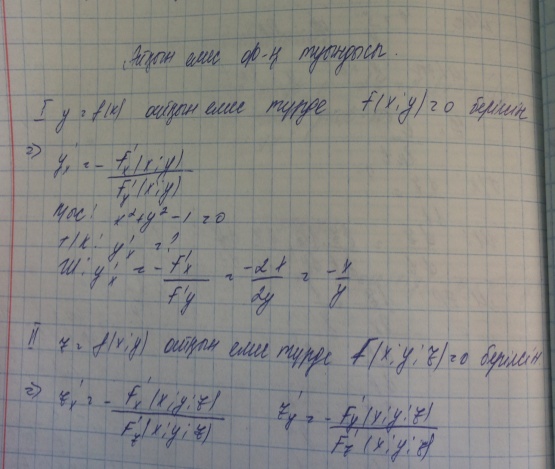
Емтихан билеті №20
1.Кез
келген периоды бар функцияны Фурье
қатарына жіктеу.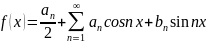 мұндағы
мұндағы
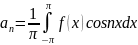 ,
,
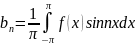
2.Көп айнымалылы функция. Егер D облысында бір -бірінен тəуелсіз х,у айнымалыларының мəндер жұбына z айнымалының анықталған бір мəні сəйкес келсе , онда z айнымалы х жəне у айнымалыларына тəуелді екі айнымалылы функция деп аталады жəне оны f(x,y)=z деп белгілейді .
Z=f(x,y)
функциясы анықталатын х жəне у қос
мəндерінің (x,y) жиынын осы функцияның
анықталу
облысы (аймағы)
деп атайды.
Z=f(x,y
) функциясының анықталу облысы Оху
жазықтығындағы нүктелер жиыны болады.
Дербес жағдайда , бүкіл Оху жазықтығы
не Оху жазықтығының тұйық сызықтармен
шектелген бөлігі немесе осы жазықтықтың
бірнеше бөліктерінің жиынтығы болады.
Z=f(x,y
)функциясының Оху тік бұрышты координаттар
жүйесіндегі геометриялық бейнесі (
графигі ) осы теңдеумен анықталатын
бет
болып табылады. Егер бір -бірінен
тəуелсіз
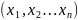 айнымалыларының
əрбір мəніне u айнымалысының анықталған
бір мəні сəйкес келсе , онда u айнымалысы
айнымалыларының
əрбір мəніне u айнымалысының анықталған
бір мəні сəйкес келсе , онда u айнымалысы айнымалыларына байланысты көп
айнымалы функция
деп аталады да
айнымалыларына байланысты көп
айнымалы функция
деп аталады да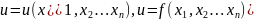 символдарымен белгіленеді .
символдарымен белгіленеді .
Күрделі көп айнымалылы функцияның туындысы.

Емтихан билеті №19
1.Фурье қатары. мұндағы ,
Жұп
және тақ периодтық функцияларды Фурье
қатарына жіктеу. Егер
f(x)-жұп ф\я болса, яғни f(-x)=f(x) б\а онда ол
Фурье қатарында sin nx болмайды.
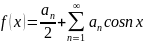 мұндағы
мұндағы
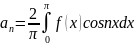 Егер f(x)-тақ
ф\я болса, яғни f(-x)=-f(x) б\а онда ол
Егер f(x)-тақ
ф\я болса, яғни f(-x)=-f(x) б\а онда ол
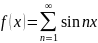
Мұндағы
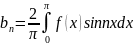
2.Үш
еселі интегралдың механикада қолданылуы.
Vденесінің көлемі
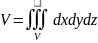
формуласымен
есептеледі. Тығыздығы
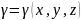 болатын
V денесінің массасы
болатын
V денесінің массасы
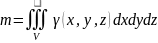 ал
Oxz Oxy Oyz , , жазықтықтарына қарағандағы
статикалық моменттері сəйкесінше
ал
Oxz Oxy Oyz , , жазықтықтарына қарағандағы
статикалық моменттері сəйкесінше
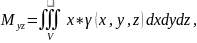
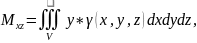
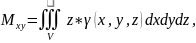 формуласымен есептелінеді.Біртекті
дене үшін const= γ Дененің ауырлық центрінің
координаттары
формуласымен есептелінеді.Біртекті
дене үшін const= γ Дененің ауырлық центрінің
координаттары
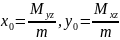 ,
,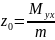 формулаларымен анықталады. Ox,Oy,Oz
осьтеріне жəне О нүктесіне қарағандағы
инерция моменттері ( екпіндік қарымдары
) сəйкес
формулаларымен анықталады. Ox,Oy,Oz
осьтеріне жəне О нүктесіне қарағандағы
инерция моменттері ( екпіндік қарымдары
) сəйкес
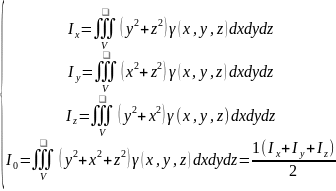 формулаларымен
есептеледі .
формулаларымен
есептеледі .
Емтихан билеті №18
1.Көп
айнымалылы функцияның дербес және
толық өсімшелері.
Z=f(x,y)
функциясымен анықталған бетті
қарастырайық. Оны const y = жазықтығымен
қияйық. Бұл жазықтықта у -тұрақты , х
айнымалысына x ∆ өсімшесін берейік .
Сонда х
айнымалысы бойынша
z
функциясының z x∆ дербес өсімшесі
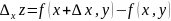 формуласымен
анықталады. Сол сияқты
Z=f(x,y)
функциясы үшін х – тұрақты болып , ал
у
айнымалысы бойынша у ∆ өсімшесін алса
, онда у айнымалысы бойынша дербес
өсімшесі
формуласымен
анықталады. Сол сияқты
Z=f(x,y)
функциясы үшін х – тұрақты болып , ал
у
айнымалысы бойынша у ∆ өсімшесін алса
, онда у айнымалысы бойынша дербес
өсімшесі
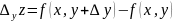 формуласымен
анықталады. Егер х жəне у айнымалылары
бойынша x ∆ жəне у ∆ өсімшілерін
қабылдаса , онда z функциясының толық
өсімшесі
формуласымен
анықталады. Егер х жəне у айнымалылары
бойынша x ∆ жəне у ∆ өсімшілерін
қабылдаса , онда z функциясының толық
өсімшесі
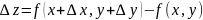 формуласымен
анықталады.
формуласымен
анықталады.
Толық
дифференциал.
 функциясының
толық өсімшесі z ∆ -ті дербес
функциясының
толық өсімшесі z ∆ -ті дербес
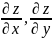 туындылары
арқылы
туындылары
арқылы
 түрінде жазуға болады , мұндағы алдыңғы
екі қосынды өсімшенің негізгі
бөлігі
, ал кейінгі екі қосынды қосалқы бөлігі
деп аталады. х ∆ жəне у ∆ шамаларымен
салыстырғанда қосалқы бөлігі жоғары
ретті шексіз аз шама болғандықтан
ұмтылғанда
түрінде жазуға болады , мұндағы алдыңғы
екі қосынды өсімшенің негізгі
бөлігі
, ал кейінгі екі қосынды қосалқы бөлігі
деп аталады. х ∆ жəне у ∆ шамаларымен
салыстырғанда қосалқы бөлігі жоғары
ретті шексіз аз шама болғандықтан
ұмтылғанда
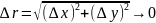 Толық өсімшенің негізгі бөлігі
функцияның
толық дифференциалы
деп аталып ,
Толық өсімшенің негізгі бөлігі
функцияның
толық дифференциалы
деп аталып ,

деп
белгіленеді . Мұндағы
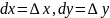

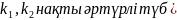
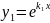
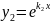
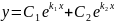
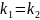 нақты
бірдей түб\р
нақты
бірдей түб\р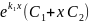
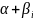 комплекс
сандар
комплекс
сандар