3. Элементы теории кодирования информации

3.1. Алфавитное кодирование информации

Ранее средства кодирования играли вспомогательную роль и не рассматривались как отдельный предмет математического изучения, но с появлением компьютеров ситуация радикально изменилась. Кодирование буквально пронизывает информационные технологии и является центральным вопросом при решении самых разных (практически всех) задач программирования:

– представление данных произвольной природы (например, чисел, текста, графики) в памяти компьютера;

– защита информации от несанкционированного доступа;

– обеспечение помехоустойчивости при передаче данных по каналам связи;

– сжатие информации в базах данных.

Теория кодирования – это раздел теории информации, изучающий способы отождествления сообщений с отображающими их сигналами.

Задача: Согласовать источник информации с каналом связи.

Объект: Дискретная или непрерывная информация, поступающая к потребителю через источник информации.

Кодирование – это преобразование информации в форму удобную для передачи по определенному каналу связи.

Примером кодирования в математике является метод координат, введенный Декартом, который дает возможность изучать геометрические объекты через их аналитическое выражение в виде чисел, букв и их комбинаций – формул.

Понятие кодирование означает преобразование информации в форму, удобную для передачи по определенному каналу связи.

Декодирование – восстановление принятого сообщения из-за кодированного вида в вид доступный для потребителя.

В общем случае задачу кодирования можно представить следующим образом. Пусть заданы два алфавита А и В, состоящие из конечного числа символов:

, .

Элементы алфавита называются буквами. Упорядоченный набор в алфавите А назовем словом

,

где , число п показывает количество букв в слове и называется длиной слова α, обозначается: п =l(α)=|α|.

Пустое слово обозначается:

Для слова

буква a₁, называется началом, или префиксом, слова α, а буква a_n – окончанием, или постфиксом, слова α. Слова можно соединять. Для этого префикс второго слова должен следовать сразу за постфиксом первого, при этом в новом слове они, естественно, утрачивают свой статус, если только одно из слов не было пустым. Соединение слов α₁ и α₂ обозначается α₁, α₂, соединение п одинаковых слов α обозначается αⁿ, причем α⁰=^. Множество всех непустых слов алфавита А обозначим А*:

Множество А называют алфавитом сообщений, а множество В – кодирующим алфавитом. Множество слов, составленных в алфавите В, обозначим В*. Обозначим через F отображение слов алфавита А в алфавит В. Тогда слово β=F(α) назовем кодом слова α.

Кодированием называют универсальный способ отображения информации при ее хранении, передаче и обработке в виде системы соответствий между элементами сообщений и сигналами, при помощи которых эти элементы можно зафиксировать. Таким образом, код – правило однозначного преобразования (т.е. функция) сообщения из одной символической формы представления (исходного алфавита А) в другую (объектный алфавит В), обычно без каких-либо потерь информации. Процесс преобразования F: А*→В* слов исходного алфавита А в алфавит В называется кодированием информации. Процесс обратного преобразования слова βЄB* в слово αЄA* называется декодированием. Таким образом, декодирование – функция, обратная F, т.е.

F-1. Так как для любого кодирования должна выполняться операция декодирования, то отображение должно быть обратимым (биекция).

Если |B|=m, то F называется m-ичным кодированием, наиболее распространенный случай В={0, 1} – двоичное кодирование. Именно этот случай и рассматривается в дальнейшем.

Если все кодовые слова имеют одинаковую длину, то код называется равномерным, или блочным.

Алфавитное (или побуквенное), кодирование можно задать таблицей кодов. Кодом или кодирующей функцией, будет служить некоторая подстановка σ. Тогда

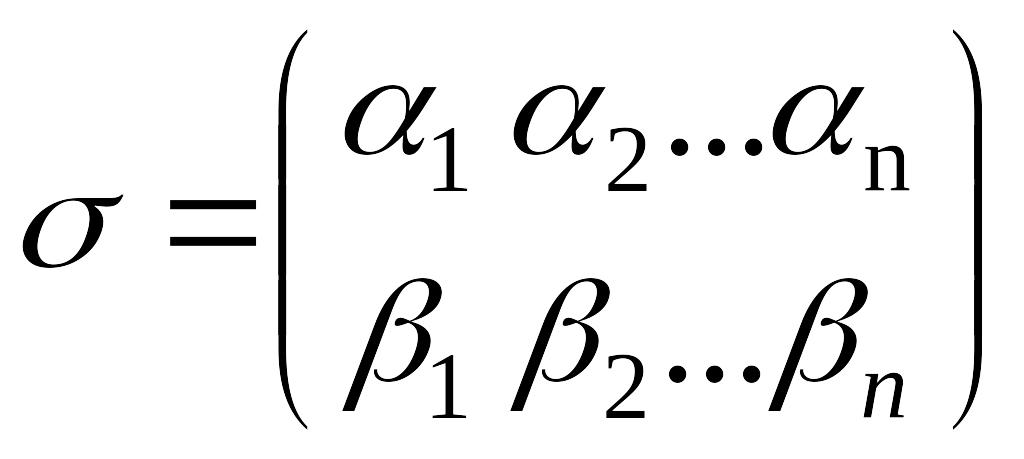
Такое побуквенное кодирование обозначается K^α_β. Множество кодов букв {β_i} называется множеством элементарных кодов. Алфавитное кодирование можно использовать для любого множества сообщений. Таким образом, алфавитное кодирование является самым простым, и его всегда можно ввести на непустых алфавитах.

Пример: Пусть заданы алфавиты

А = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, В = {0, 1}.

Тогда таблица кодирования может быть подстановкой:

.

Это двоично-десятичное кодирование, оно является взаимно-однозначным и потому допускает декодирование.

Однако схема

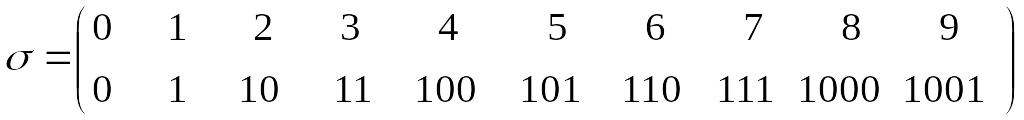
не является взаимно-однозначной. Например, набор из шести единиц 111111 может соответствовать как слову 333, так и 77, а также 111111, 137, 3311 или 7111 плюс любая перестановка.

Схема алфавитного кодирования называется префиксной, если элементарный код одной буквы не является префиксом элементарного кода другой буквы. Схема алфавитного кодирования называется разделимой, если любое слово, составленное из элементарных кодов, разлагается на элементарные коды единственным образом.

Алфавитное кодирование с разделимой схемой допускает декодирование. Можно доказать, что префиксная схема является разделимой. Для того чтобы схема алфавитного кодирования была разделимой, необходимо, чтобы длины элементарных кодов удовлетворяли соотношению, известному как неравенство Макмиллана.

Если схема алфавитного кодирования

разделима, то справедливо неравенство

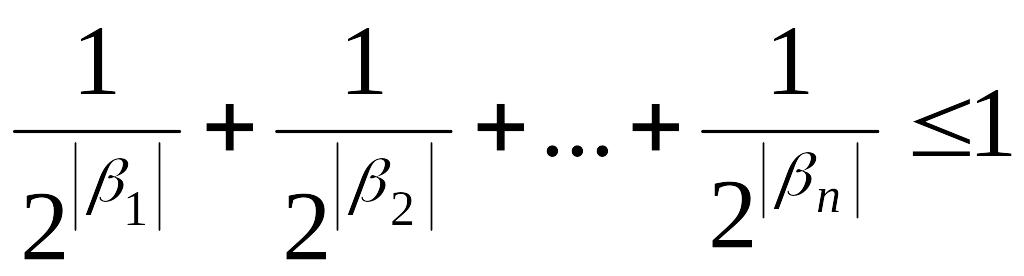
Пример: Схема алфавитного кодирования

А={а, b} и В={0, 1},

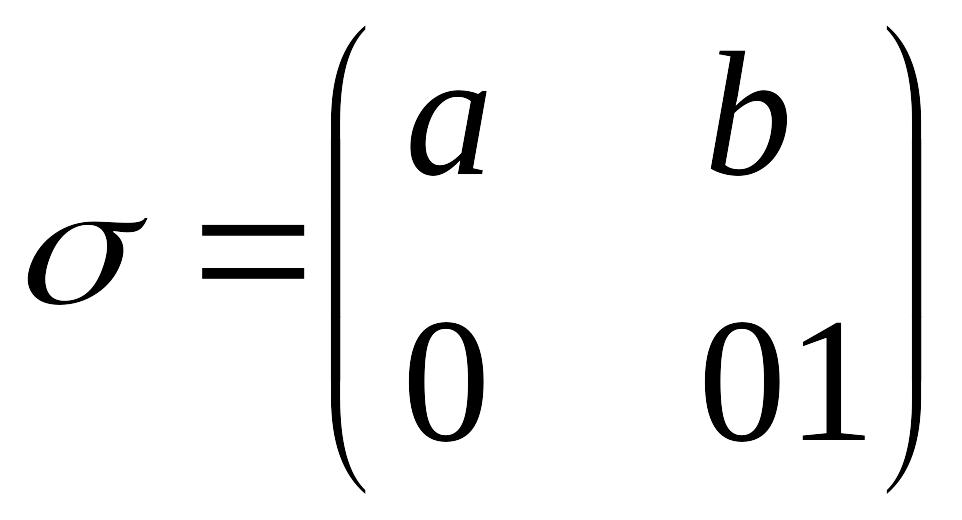
является разделимой, т.к. , ,

и, значит, выполняется неравенство Макмиллана

.

Данная схема префиксной не является, т.к. элементарный код буквы а является префиксом элементарного кода буквы b.