
- •Требования к оформлению контрольной работы
- •Вопросы к экзамену.
- •1. Введение в математический анализ
- •2. Производная и дифференциал функции
- •3. Применение производных к исследованию свойств функции
- •4. Функция нескольких переменных. Производные и дифференциалы функций нескольких переменных
- •5. Неопределенный интеграл
- •11. Степенные и функциональные ряды
- •12. Теория вероятностей и элементы математической статистики
- •Список основной литературы
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к выполнению контрольной работы
по дисциплине «Математика»
Ставрополь 2012
Методические указания к выполнению контрольной работы составлены в соответствие с требованиями государственного образовательного стандарта высшего профессионального образования и программой дисциплины «Математика» для студентов первого курса. Они содержат задания контрольной работы, а также вопросы к экзамену.
Составители: Обласова И.Н.
Формулировка задания и его объем
В контрольной работе предлагается решить 11 задач по вариантам, включающим соответствующие задания. Каждое задание (их одиннадцать) включает десять задач. Студент должен решить одну задачу из задания в соответствии со своим вариантом.
В задания включены задачи по разделам: математический анализ.
Студент должен выполнять решение задач по варианту, номер которого совпадает с двумя последними цифрами номера зачетной книжки.
В таблице приведены номера задач, предлагаемые студентам для выполнения контрольной работы. Вариант контрольной работы определяется по таблице в зависимости от двух последних цифр шифра (номера зачетной книжки) студента. В колонке таблицы по вертикали расположены цифры от 0 до 9, каждая из которых является предпоследней цифрой шифра. В верхней строке по горизонтали размещены также цифры от 0 до 9, каждая из которых является последней цифрой шифра. Пересечение вертикальной (А) и горизонтальной (В) линий определяет номера заданий контрольной работы.
А\В |
Последняя цифра шифра |
||||||||||
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
||
Предпоследняя цифра шифра |
0 |
6, 16, 24, 35, 46, 51, 66, 76, 84, 95, 106 |
4, 17, 23, 39, 50, 56, 64, 77, 83, 99, 110 |
3, 14, 29, 36, 45, 57, 63, 74, 89, 96, 105 |
9, 13, 28, 31, 41, 54, 69, 73, 88, 91, 101 |
1, 20, 30, 33, 43, 55, 61, 80, 90, 93, 103 |
10, 12, 22, 32, 49, 53, 70, 72, 82, 92, 109 |
2, 18, 21, 38, 42, 60, 62, 78, 81, 98, 102 |
8, 19, 27, 34, 48, 52, 68, 79, 87, 94, 108 |
7, 15, 26, 37, 47, 58, 67, 75, 86, 97, 107 |
5, 11, 25, 40, 44, 59, 65, 71, 85, 100, 104 |
1 |
4, 20, 27, 33, 43, 54, 64, 80, 87, 93, 103 |
1, 12, 21, 37, 45, 56, 61, 72, 81, 97, 105 |
9, 19, 25, 31, 41, 55, 69, 79, 85, 91, 101 |
7, 17, 23, 34, 47, 59, 67, 77, 83, 94, 107 |
5, 16, 22, 40, 50, 58, 65, 76, 82, 100, 110 |
8, 14, 30, 38, 46, 57, 68, 74, 90, 98, 106 |
6, 18, 24, 35, 48, 60, 66, 78, 84, 95, 108 |
10, 13, 26, 32, 44, 52, 70, 73, 86, 92, 104 |
3, 15, 29, 39, 49, 51, 63, 75, 89, 99, 109 |
2, 11, 28, 36, 42, 53, 62, 71, 88, 96, 102 |
|
2 |
5, 16, 26, 38, 45, 60, 65, 76, 86, 98, 105 |
2, 19, 29, 32, 43, 57, 62, 79, 89, 92, 103 |
9, 12, 22, 39, 44, 56, 69, 72, 82, 99, 104 |
4, 17, 27, 34, 47, 54, 64, 77, 87, 94, 107 |
1, 20, 30, 31, 49, 51, 61, 80, 90, 91, 109 |
6, 15, 25, 37, 46, 52, 66, 75, 85, 97, 106 |
7, 14, 24, 36, 42, 53, 67, 74, 84, 96, 102 |
8, 13, 23, 35, 48, 55, 68, 73, 83, 95, 108 |
3, 18, 28, 33, 41, 58, 63, 78, 88, 93, 101 |
10, 11, 21, 40, 50, 59, 70, 71, 81, 100, 110 |
|
3 |
5, 16, 26, 31, 45, 54, 65, 76, 86, 91, 105 |
4, 15, 25, 32, 50, 56, 64, 75, 85, 92, 110 |
7, 20, 28, 36, 46, 55, 67, 80, 88, 96, 106 |
3, 14, 24, 33, 41, 60, 63, 74, 84, 93, 101 |
9, 19, 30, 39, 43, 57, 69, 79, 90, 99, 103 |
6, 17, 27, 35, 48, 53, 66, 77, 87, 95, 108 |
2, 11, 22, 38, 47, 52, 62, 71, 82, 98, 107 |
10, 18, 29, 40, 44, 58, 70, 78, 89, 100, 104 |
1, 12, 23, 34, 42, 59, 61, 72, 83, 94, 102 |
8, 13, 21, 37, 49, 51, 68, 73, 81, 97, 109 |
|
4 |
6, 14, 27, 34, 47, 51, 66, 74, 87, 94, 107 |
5, 20, 25, 33, 50, 59, 62, 73, 88, 97, 106 |
2, 13, 28, 37, 46, 54, 65, 80, 85, 93, 110 |
10, 17, 24, 32, 41, 58, 70, 77, 84, 92, 101 |
1, 15, 29, 38, 45, 53, 61, 75, 89, 98, 105 |
4, 12, 23, 35, 42, 55, 64, 72, 83, 95, 102 |
3, 16, 26, 40, 44, 52, 63, 76, 86, 100, 104 |
8, 18, 22, 36, 48, 57, 68, 78, 82, 96, 108 |
9, 11, 30, 39, 43, 56, 69, 71, 90, 99, 103 |
7, 19, 21, 31, 49, 60, 67, 79, 81, 91, 109 |
|
5 |
10, 12, 21, 37, 48, 53, 70, 72, 81, 97, 108 |
9, 18, 22, 38, 41, 54, 69, 78, 82, 98, 101 |
8, 19, 23, 36, 46, 55, 68, 79, 83, 96, 106 |
7, 17, 25, 35, 45, 56, 67, 77, 85, 95, 105 |
1, 11, 30, 39, 44, 57, 61, 71, 90, 99, 104 |
5, 15, 26, 33, 49, 60, 65, 75, 86, 93, 109 |
4, 14, 27, 32, 43, 58, 64, 74, 87, 92, 103 |
3, 13, 28, 31, 50, 59, 63, 73, 88, 91, 110 |
2, 20, 29, 40, 47, 52, 62, 80, 89, 100, 107 |
6, 16, 24, 34, 42, 51, 66, 76, 84, 94, 102 |
|
6 |
9, 20, 21, 35, 48, 51, 69, 80, 81, 95, 108 |
4, 18, 24, 37, 47, 52, 64, 78, 84, 97, 107 |
5, 17, 27, 33, 50, 59, 65, 77, 87, 93, 110 |
6, 14, 22, 39, 44, 55, 66, 74, 82, 99, 104 |
8, 16, 25, 31, 43, 56, 68, 76, 85, 91, 103 |
10, 19, 29, 38, 42, 57, 70, 79, 89, 98, 102 |
7, 11, 23, 36, 46, 53, 67, 71, 83, 96, 106 |
3, 15, 26, 32, 41, 58, 63, 75, 86, 92, 101 |
1, 13, 30, 34, 45, 54, 61, 73, 90, 94, 105 |
2, 12, 28, 40, 49, 60, 62, 72, 88, 100, 109 |
|
7 |
10, 15, 27, 32, 46, 58, 70, 75, 87, 92, 106 |
6, 17, 26, 39, 41, 56, 66, 77, 86, 99, 101 |
7, 20, 22, 36, 47, 59, 67, 80, 82, 96, 107 |
1, 11, 29, 35, 45, 57, 61, 71, 89, 95, 105 |
9, 19, 23, 34, 48, 60, 69, 79, 83, 94, 108 |
8, 18, 24, 33, 50, 55, 68, 78, 84, 93, 110 |
2, 12, 30, 38, 42, 54, 62, 72, 90, 98, 102 |
3, 13, 28, 40, 44, 53, 63, 73, 88, 100, 104 |
5, 16, 25, 31, 43, 52, 65, 76, 85, 91, 103 |
4, 14, 21, 37, 49, 51, 64, 74, 81, 97, 109 |
|
8 |
8, 17, 21, 36, 46, 54, 68, 77, 81, 96, 106 |
10, 11, 23, 37, 48, 55, 70, 71, 83, 97, 108 |
6, 20, 24, 33, 43, 51, 66, 80, 84, 93, 103 |
9, 16, 22, 38, 47, 60, 69, 76, 82, 98, 107 |
5, 19, 25, 39, 50, 53, 65, 79, 85, 99, 110 |
7, 18, 27, 40, 49, 52, 67, 78, 87, 100, 109 |
1, 12, 30, 35, 45, 56, 61, 72, 90, 95, 105 |
3, 15, 28, 31, 41, 57, 63, 75, 88, 91, 101 |
4, 14, 26, 32, 44, 58, 64, 74, 86, 92, 104 |
2, 13, 29, 34, 42, 59, 62, 73, 89, 94, 102 |
|
9 |
8, 19, 28, 38, 44, 54, 68, 79, 88, 98, 104 |
4, 16, 21, 34, 42, 52, 64, 76, 81, 94, 102 |
10, 11, 29, 36, 47, 57, 70, 71, 89, 96, 107 |
3, 13, 27, 31, 50, 60, 63, 73, 87, 91, 110 |
7, 12, 23, 35, 46, 56, 67, 72, 83, 95, 106 |
5, 14, 22, 37, 45, 55, 65, 74, 82, 97, 105 |
6, 20, 26, 40, 49, 59, 66, 80, 86, 100, 109 |
1, 15, 30, 32, 43, 53, 61, 75, 90, 92, 103 |
2, 17, 25, 33, 48, 58, 62, 77, 85, 93, 108 |
9, 18, 24, 39, 41, 51, 69, 78, 84, 99, 101 |
|
Задания.
1. Исследовать на экстремум функции.
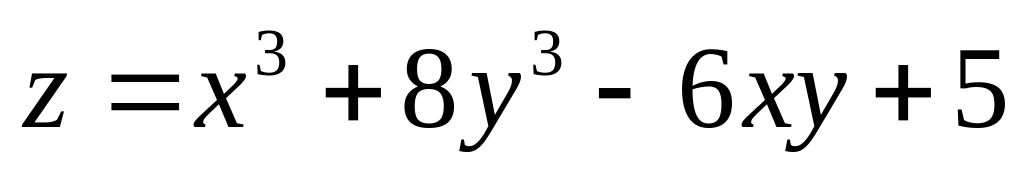 ;
;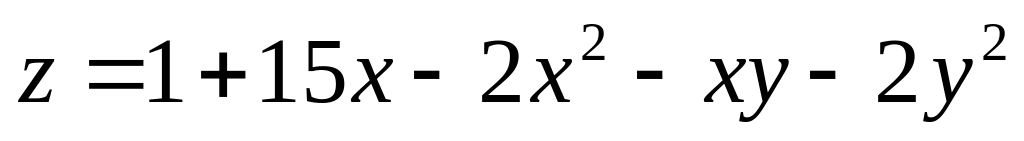 ;
;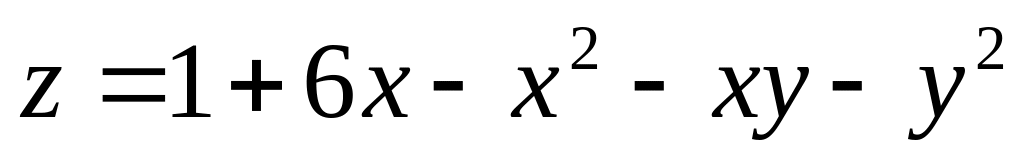 ;
;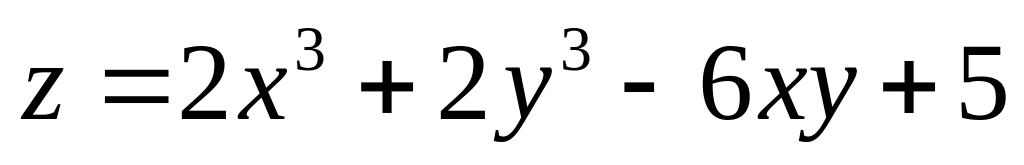 ;
;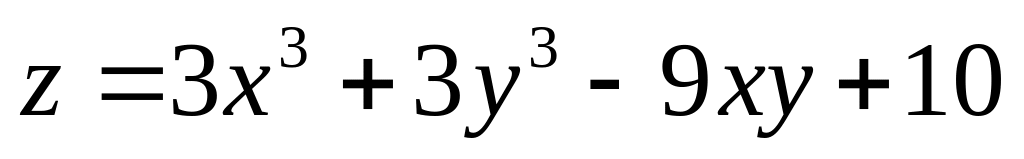 ;
;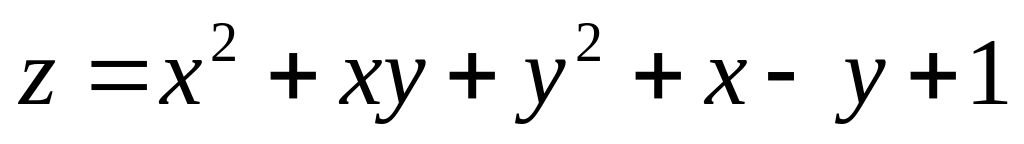 ;
;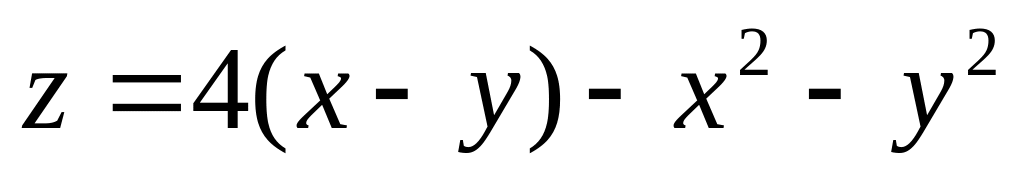 ;
;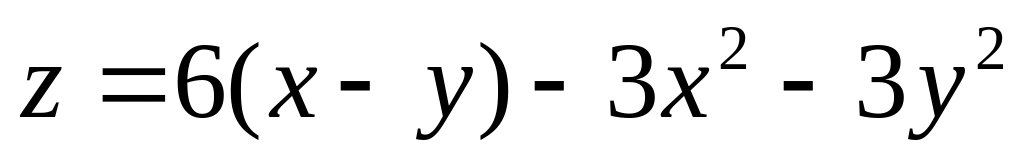 ;
;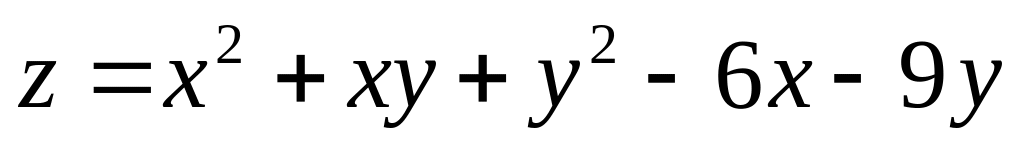 ;
;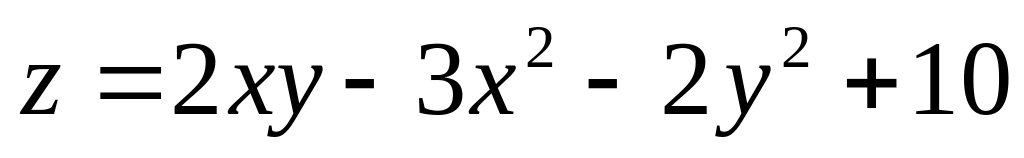 .
.
2. Найти
наибольшее и наименьшее значения функции
![]() в замкнутой области
в замкнутой области
![]() ,
заданной системой неравенств.
,
заданной системой неравенств.
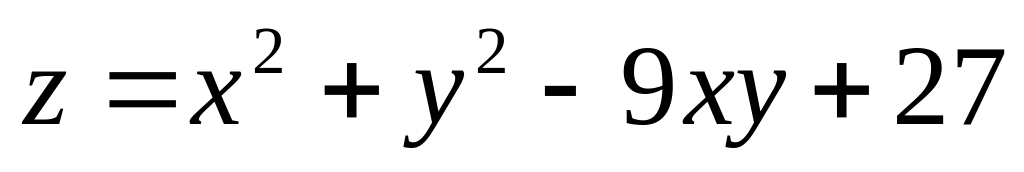 ;
;
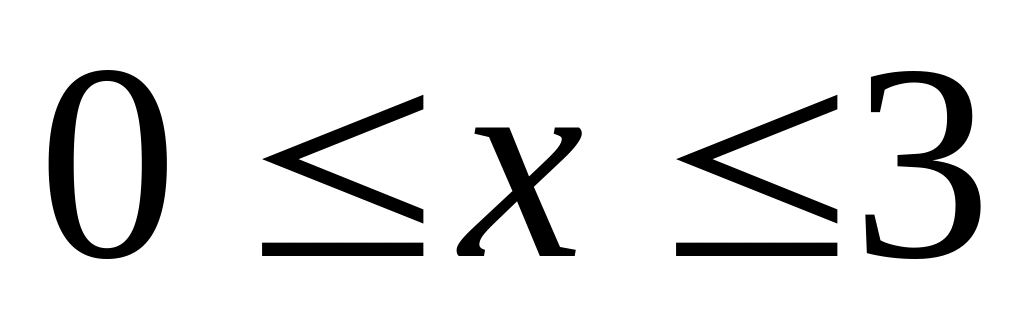 ,
,
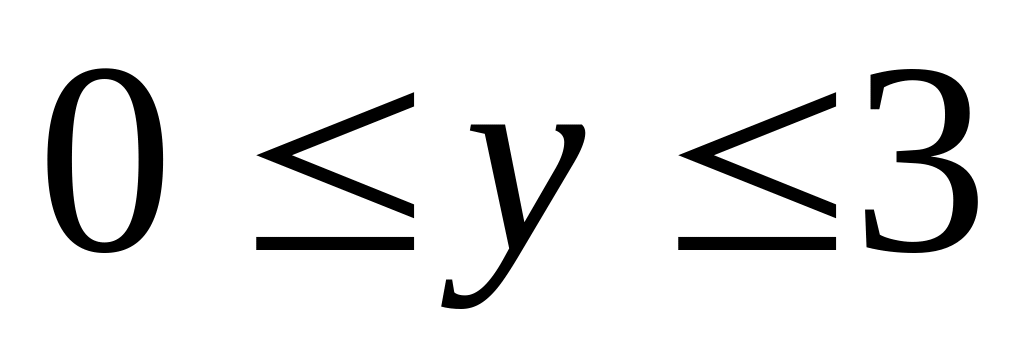 .
.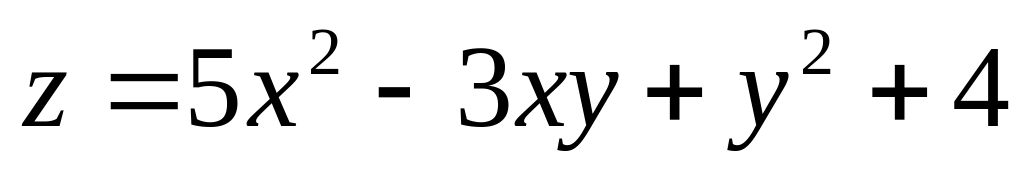 ;
;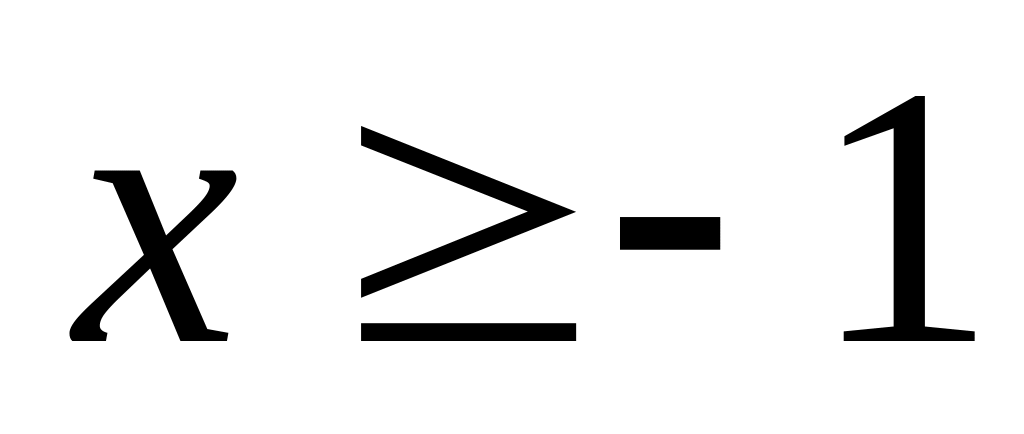 ,
,
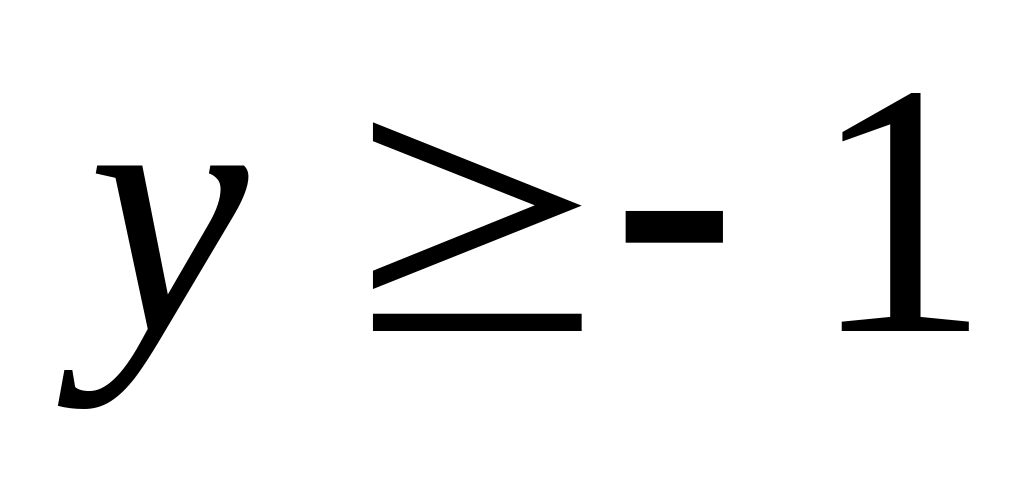 ,
,
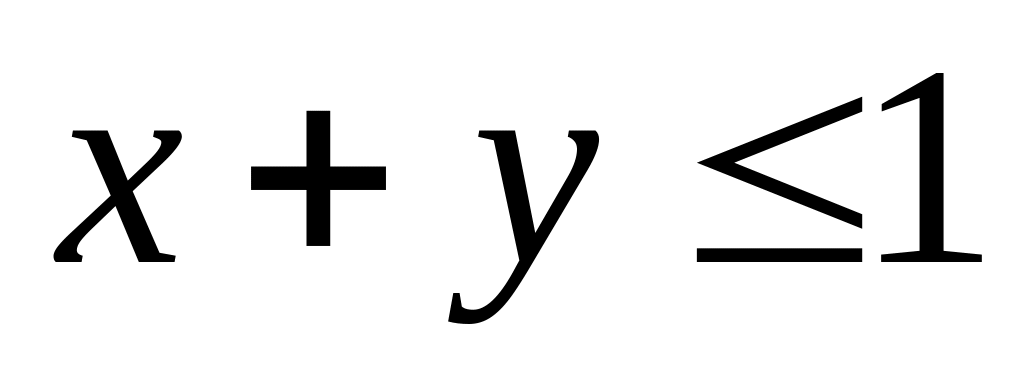 .
.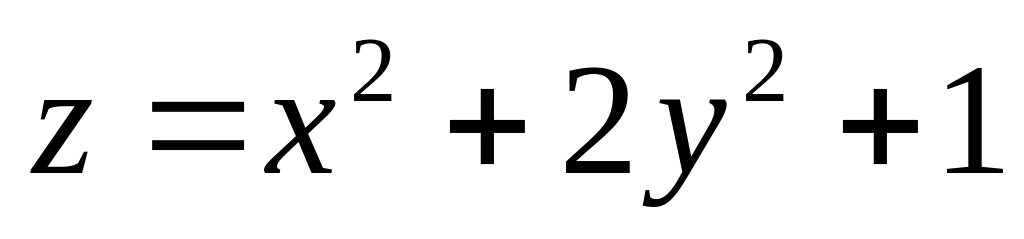 ;
;
 ,
,
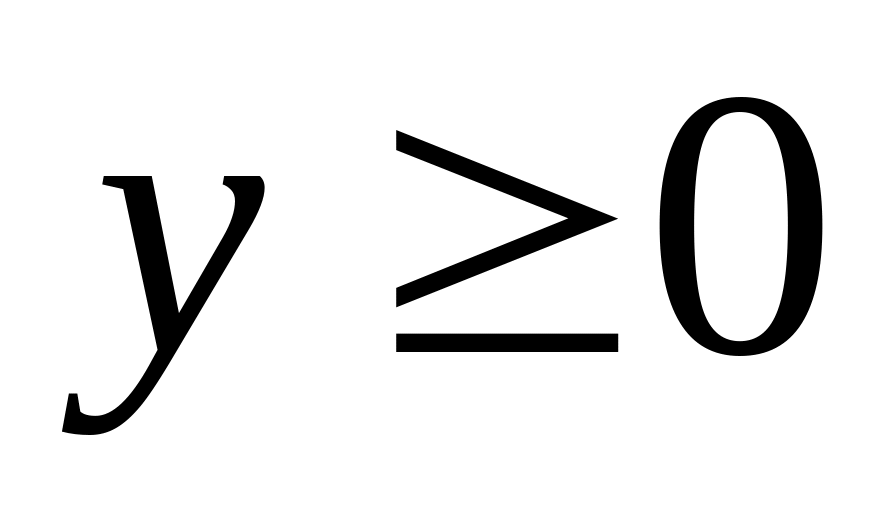 ,
,
 .
.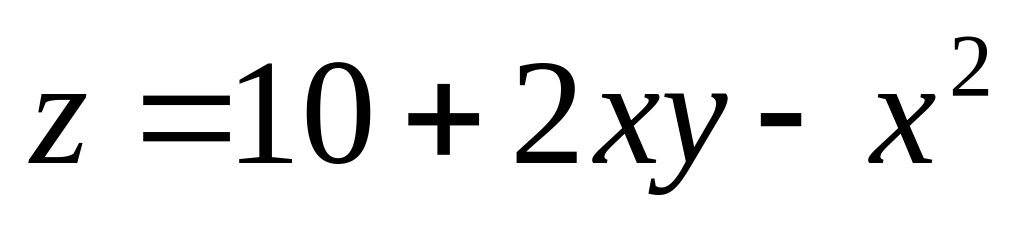 ;
;
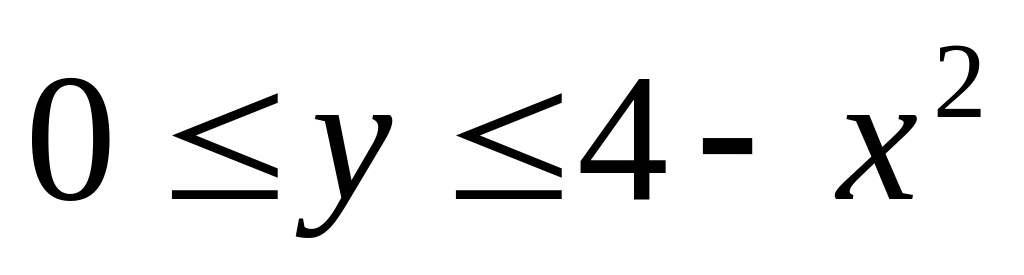 .
.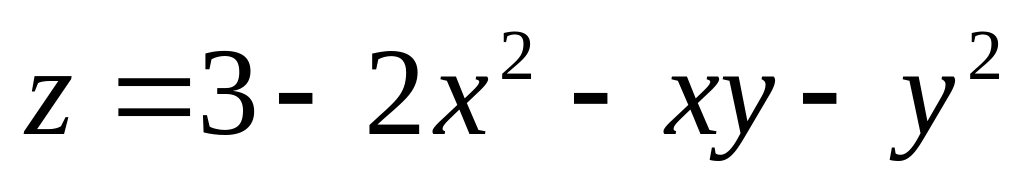 ;
;
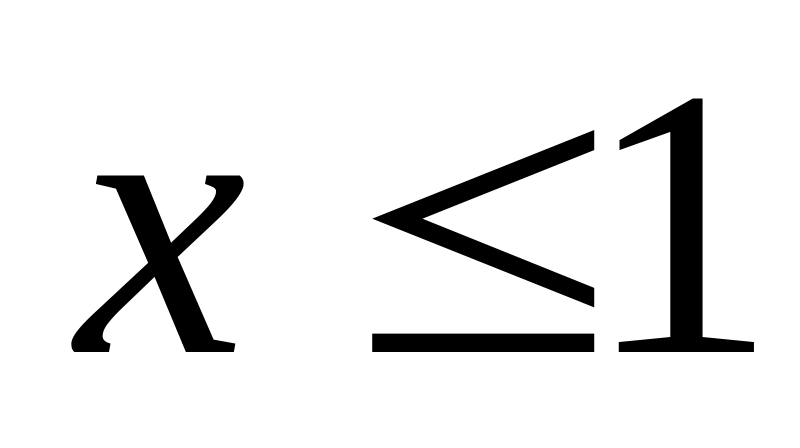 ,
,
,
,
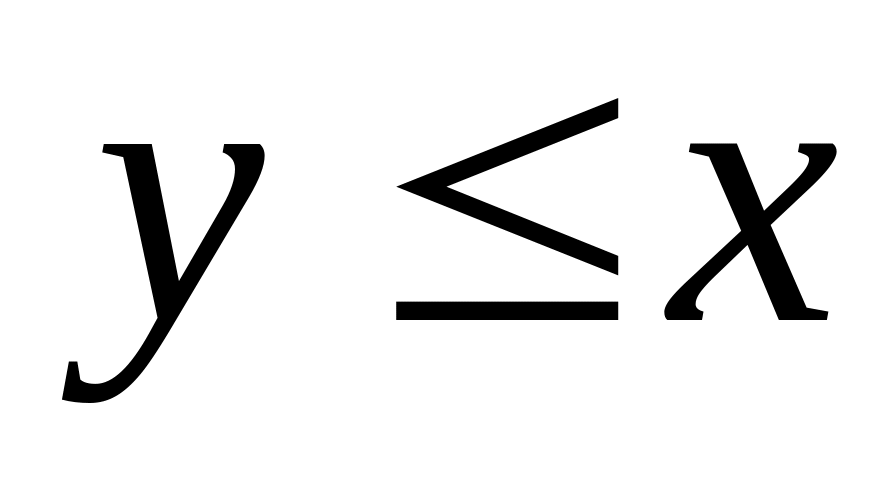 .
.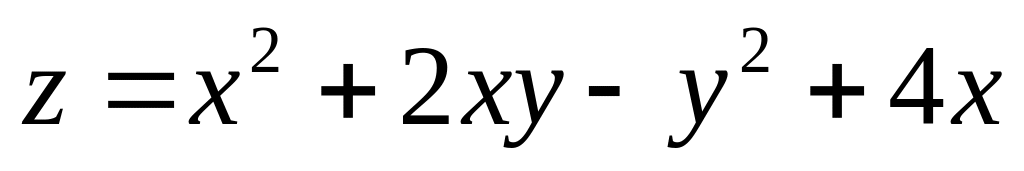 ;
;
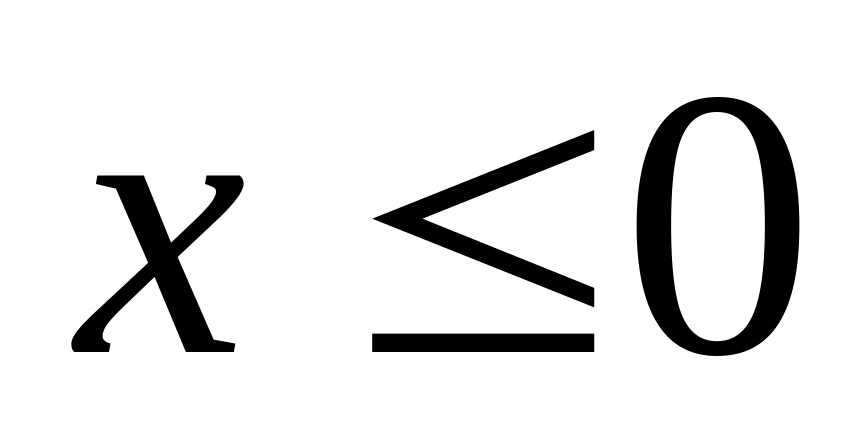 ,
,
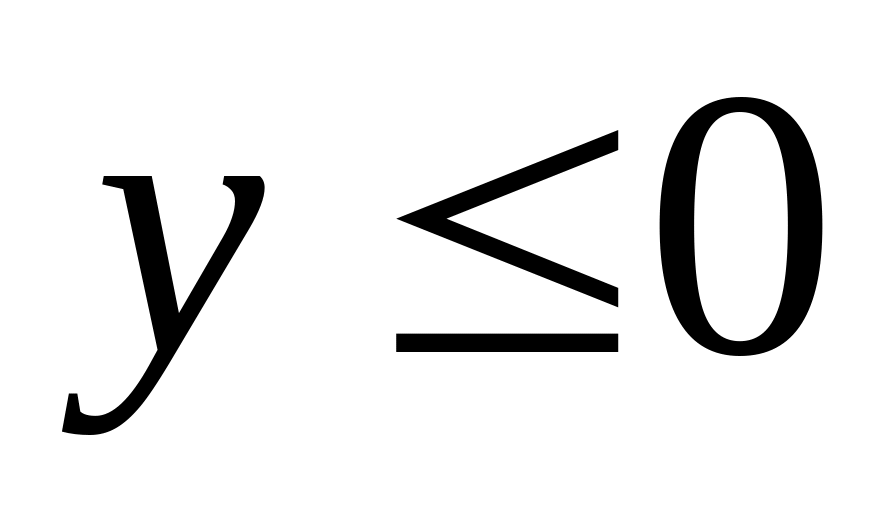 ,
,
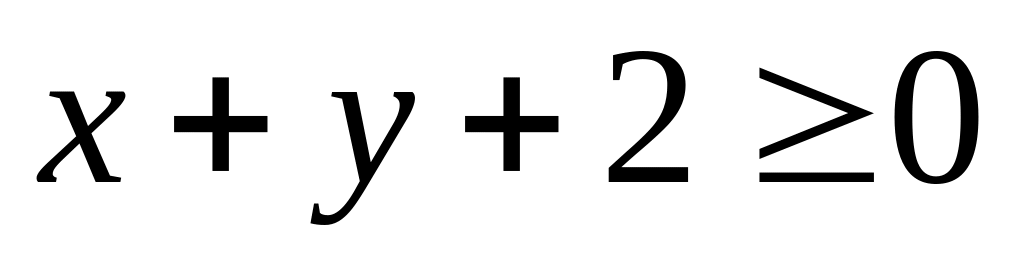 .
.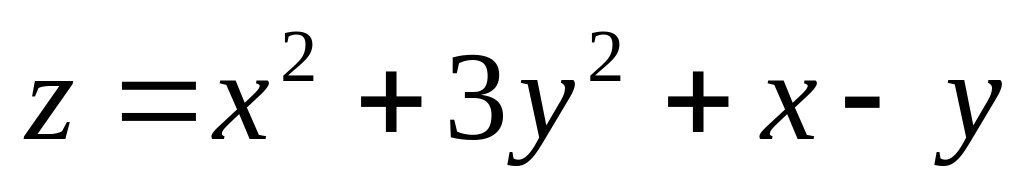 ;
,
,
.
;
,
,
.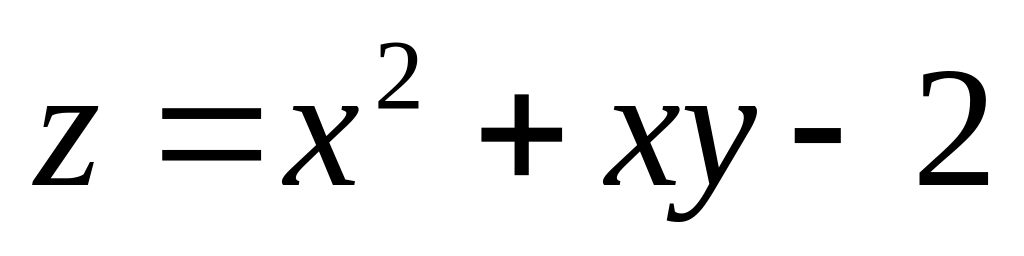 ;
;
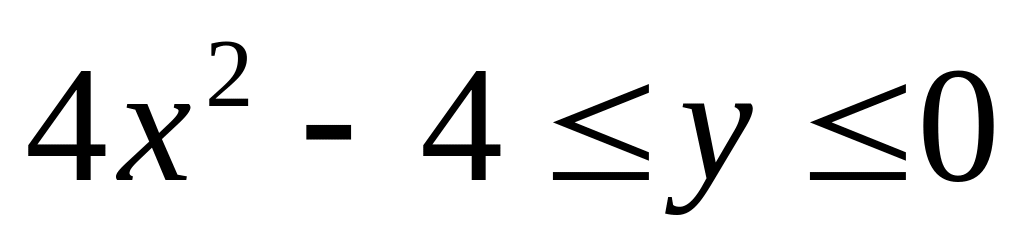 .
. ;
;
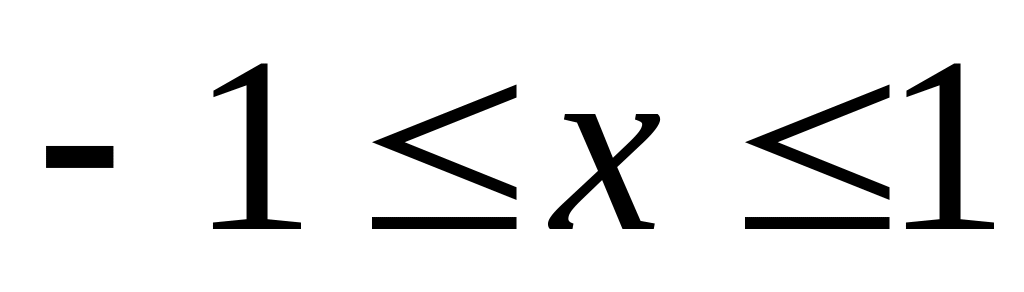 ,
,
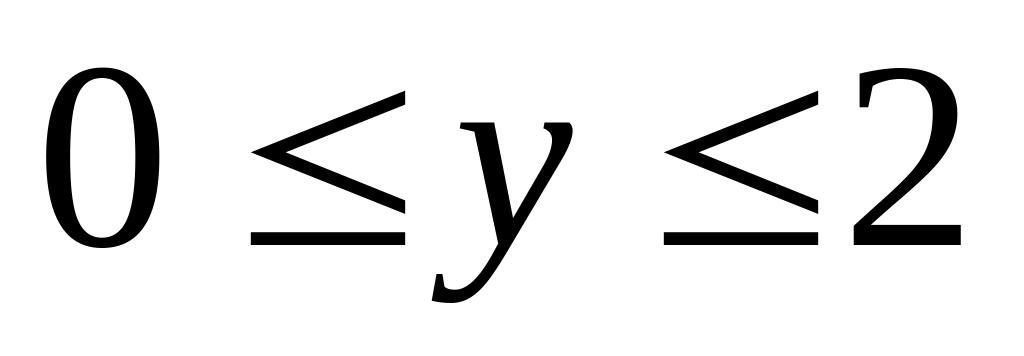 .
.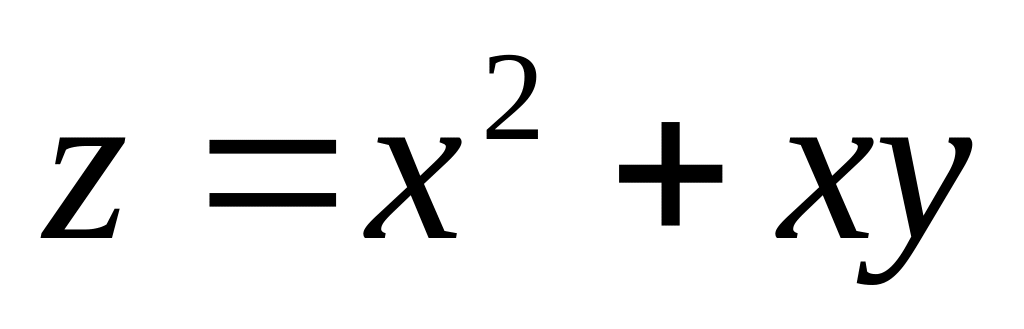 ;
,
.
;
,
.
3. Найти неопределенные интегралы. В пунктах а) и б) результаты проверить дифференцированием.
а)
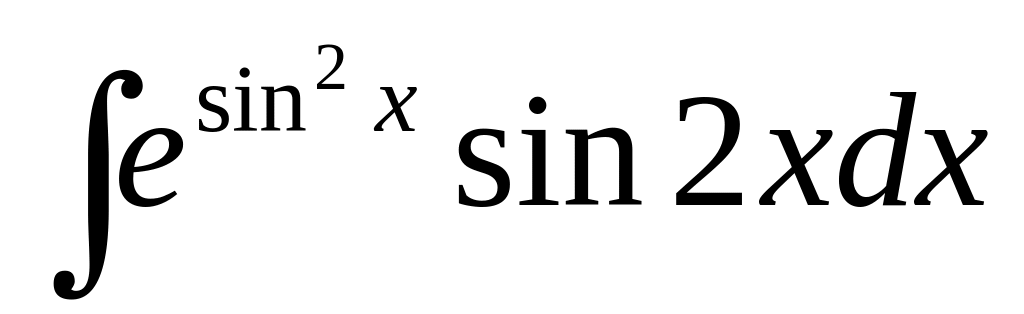 ,
б)
,
б) ,
в)
,
в)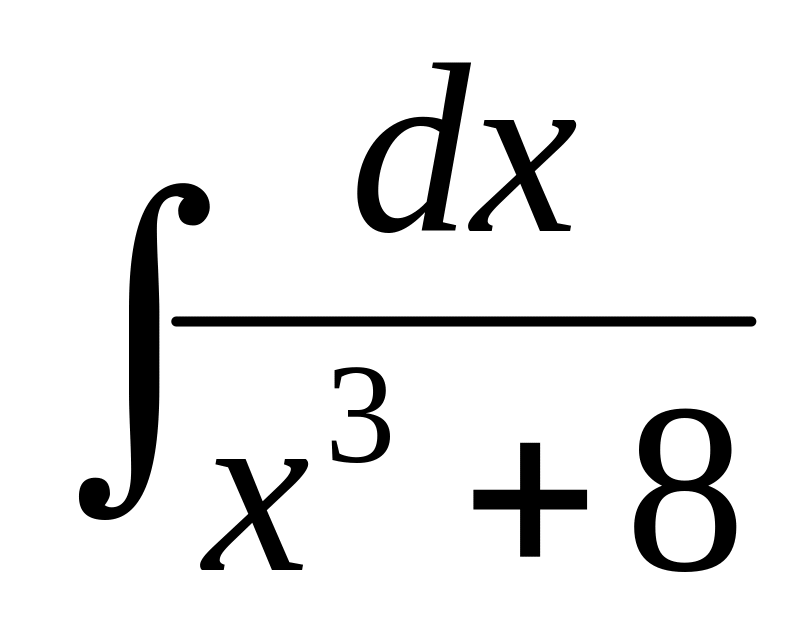 ,
г)
,
г)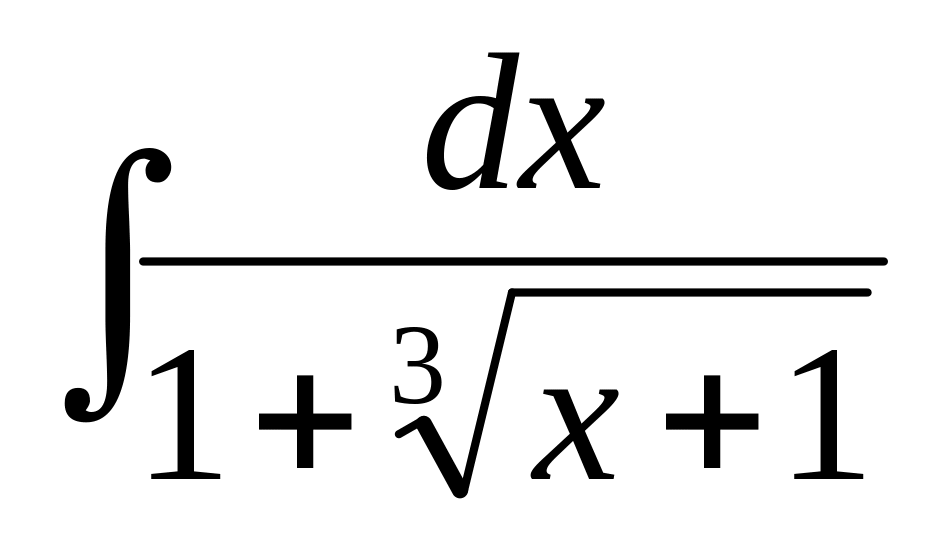 .
.а)
 ,
б)
,
б) ,
в)
,
в)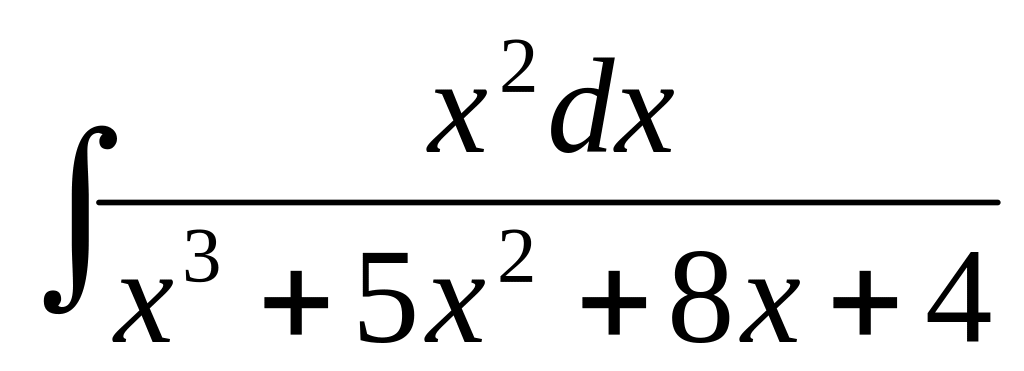 ,
г)
,
г)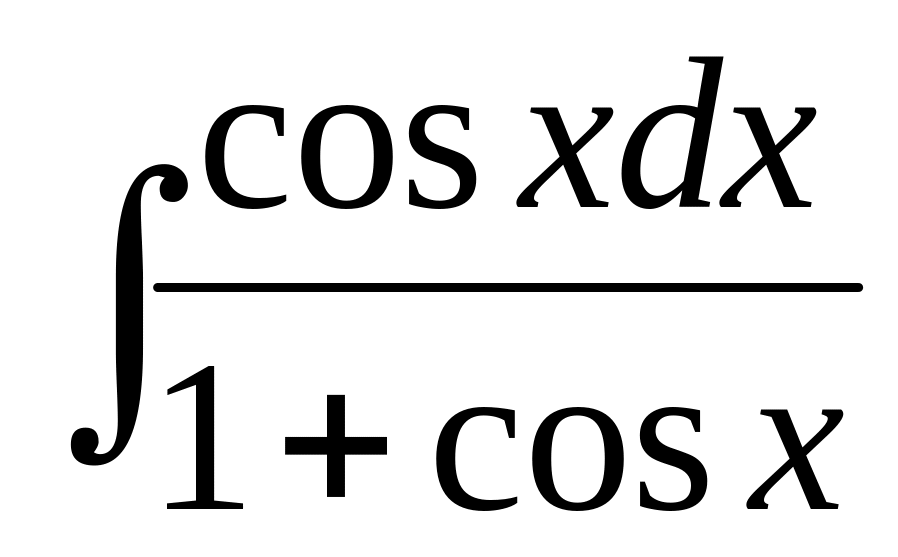 .
.а)
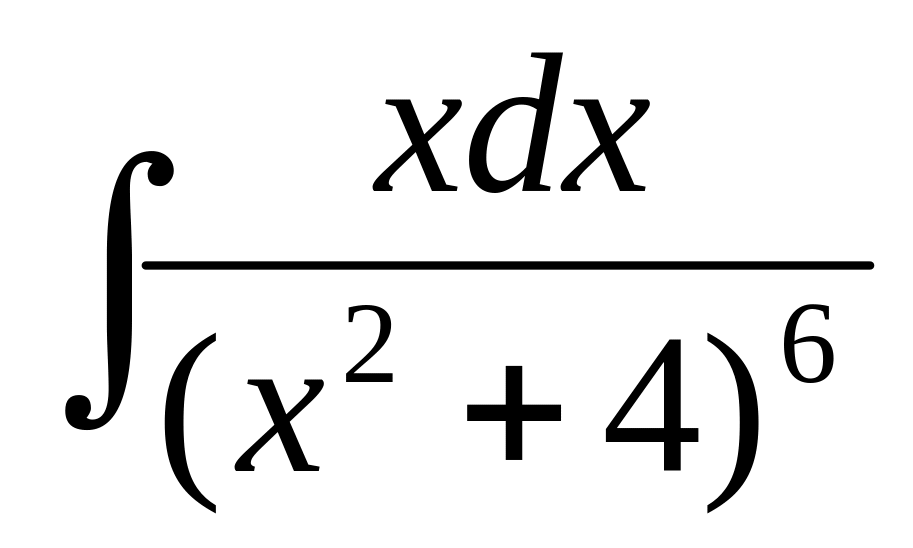 ,
б)
,
б)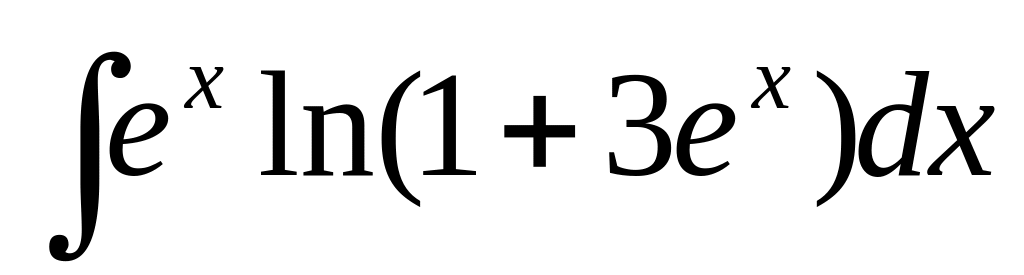 ,
в)
,
в)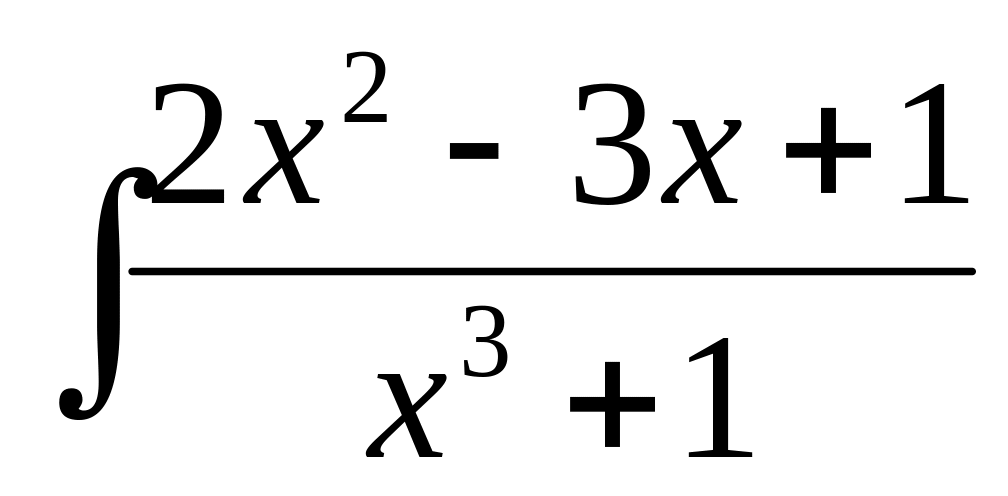 ,
г)
,
г)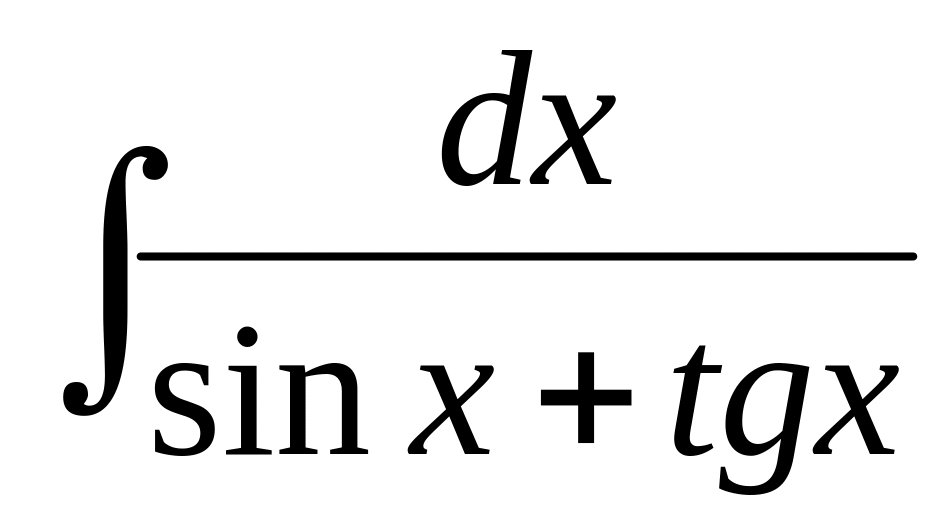 .
.а)
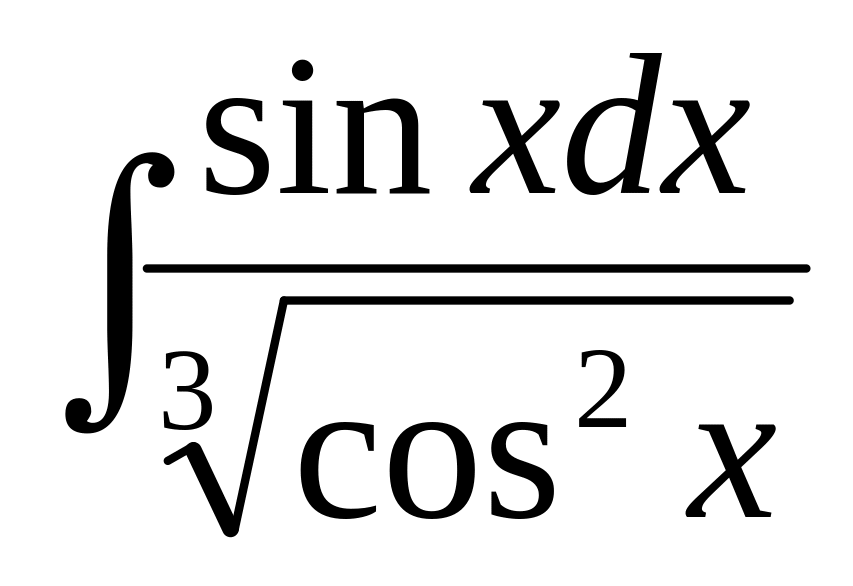 ,
б)
,
б)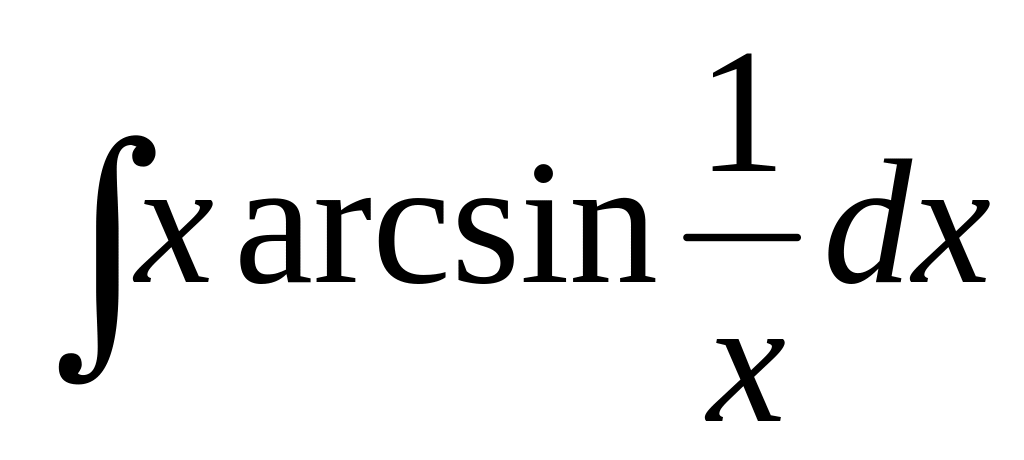 ,
в)
,
в)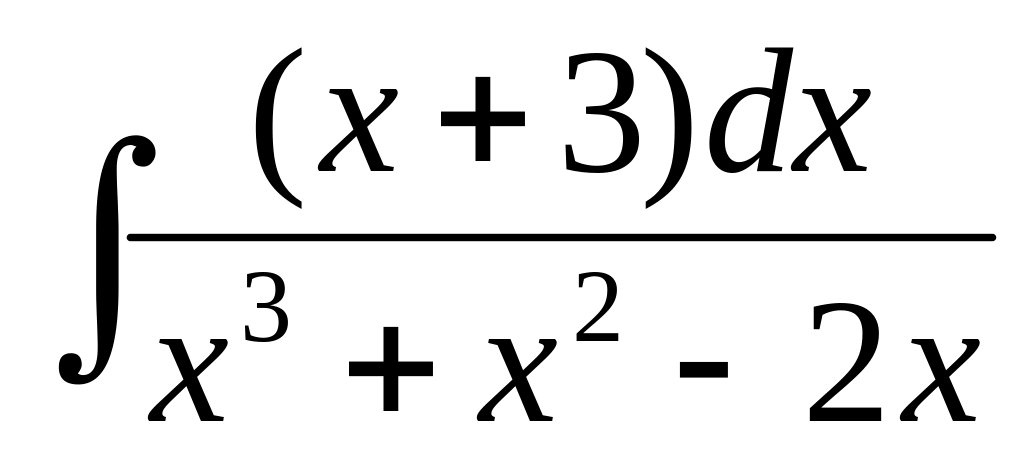 ,
г)
,
г)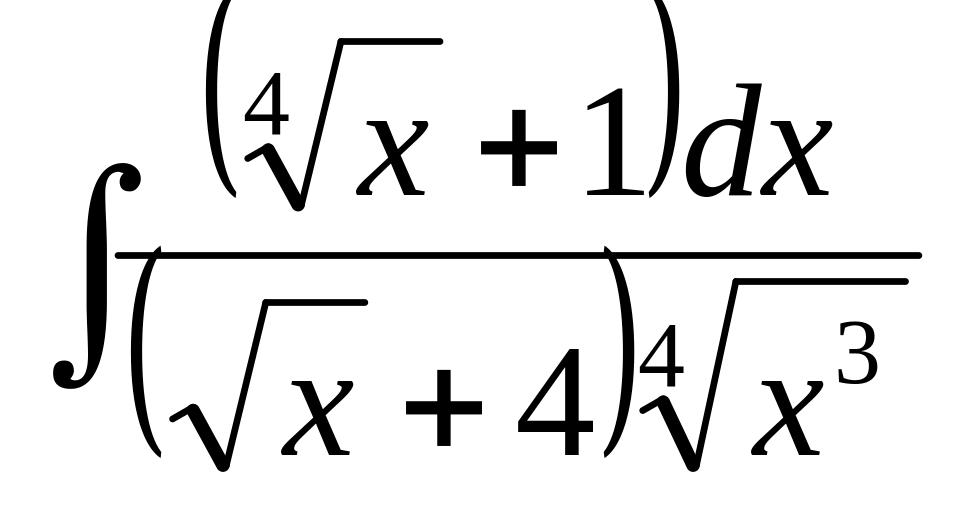 .
.а)
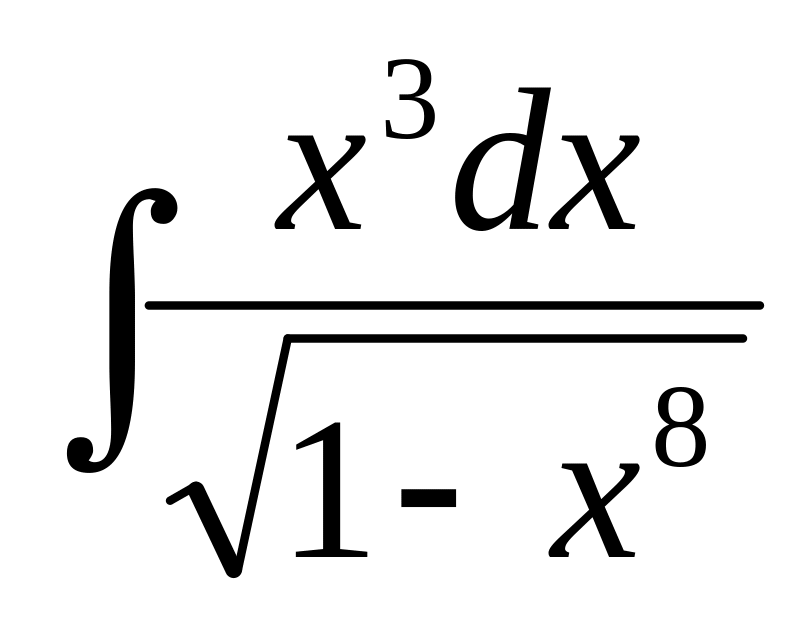 ,
б)
,
б) ,
в)
,
в)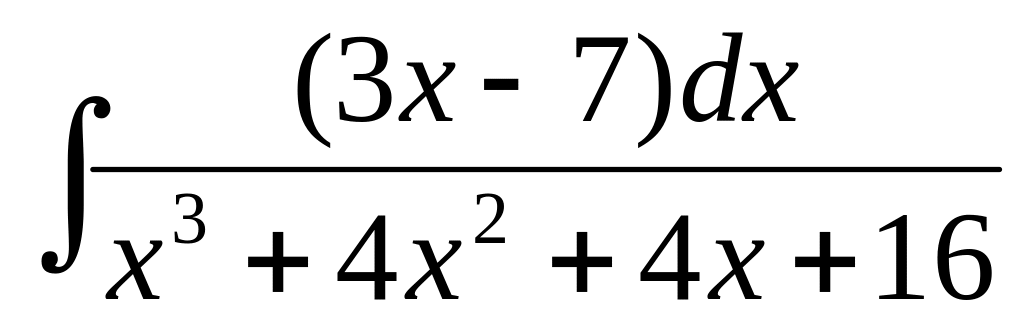 ,
г)
,
г)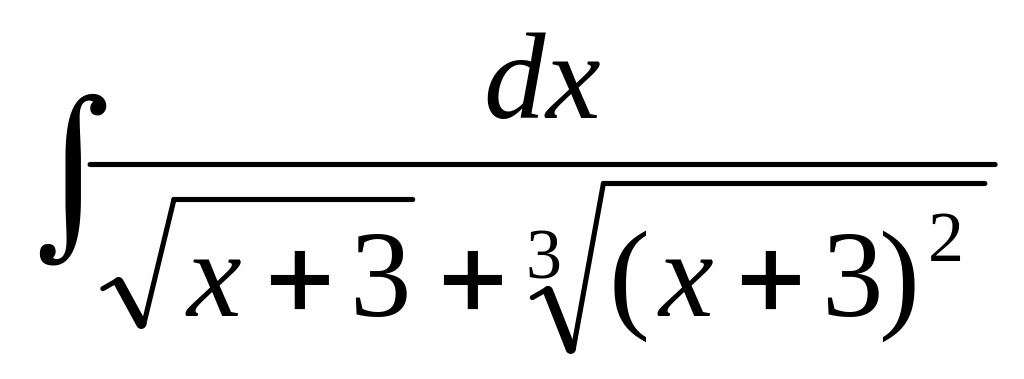 .
.а)
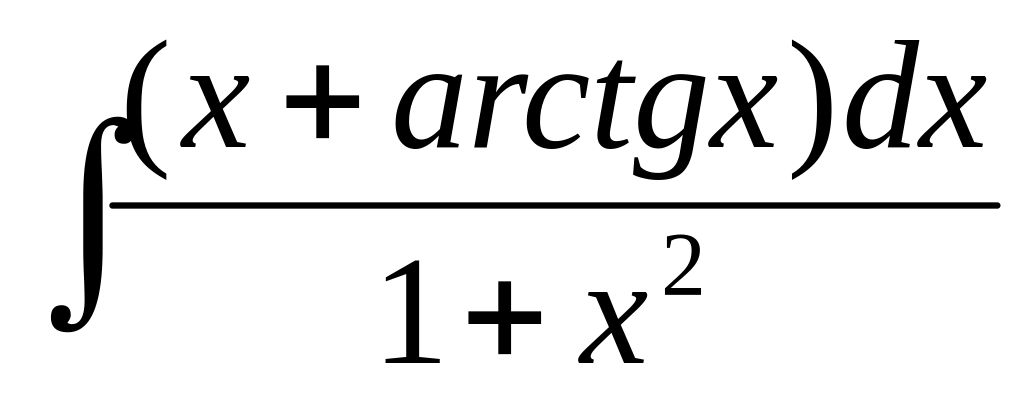 ,
б)
,
б)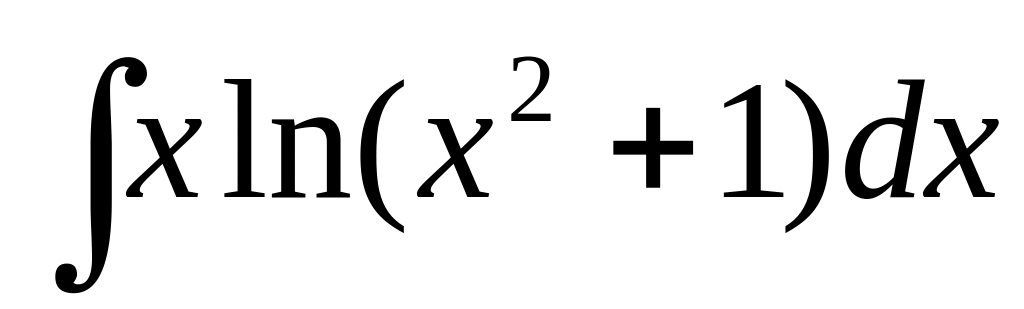 ,
в)
,
в)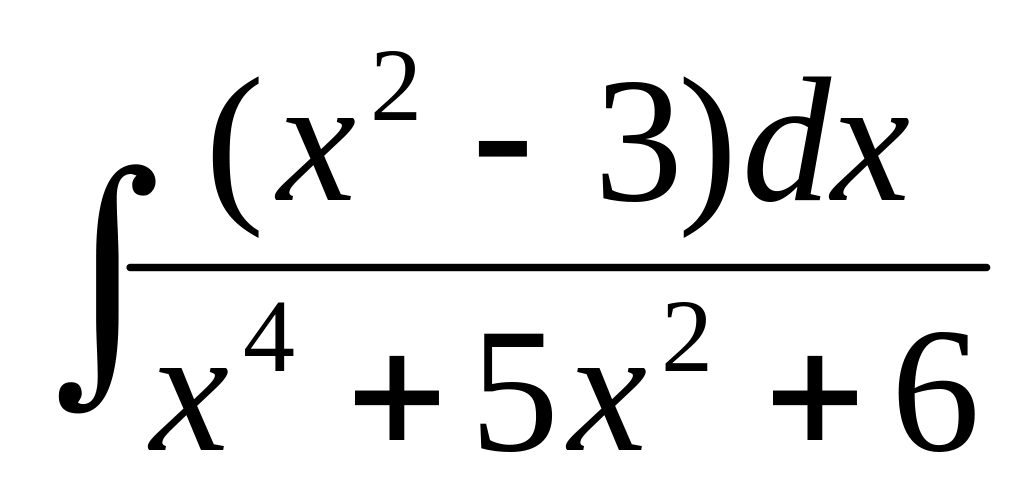 ,
г)
,
г)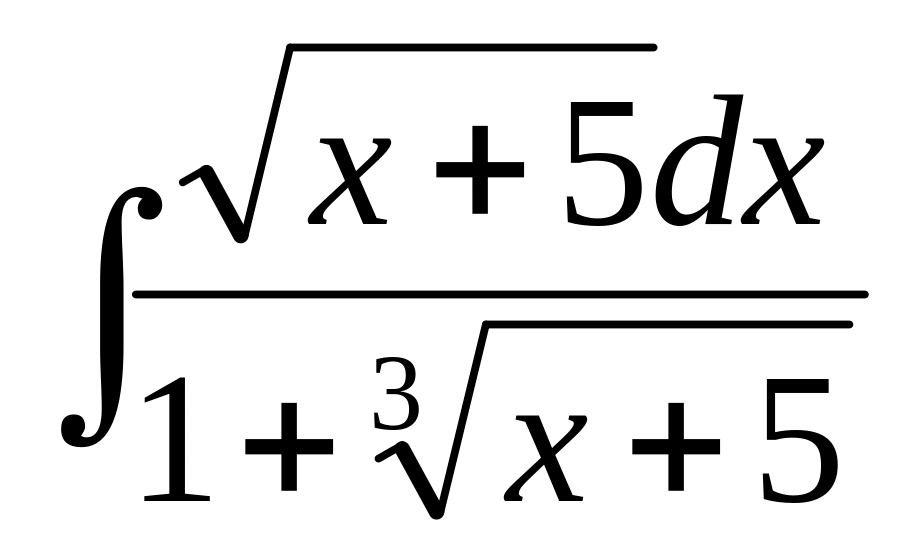 .
.а)
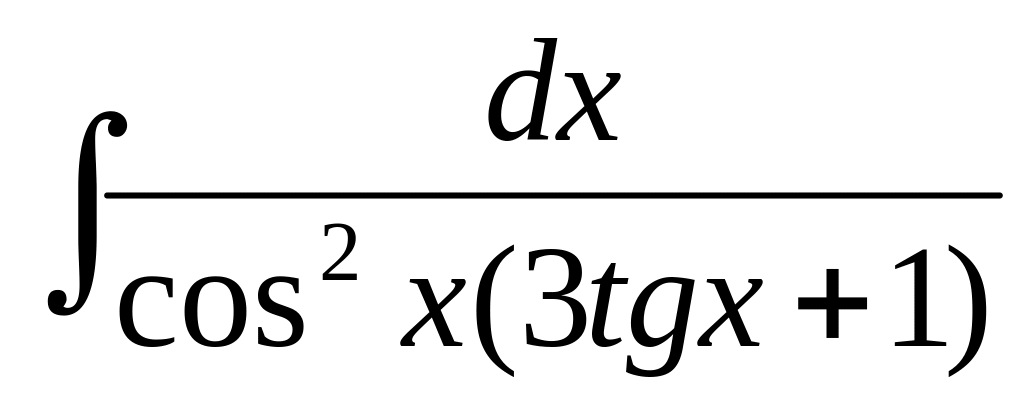 ,
б)
,
б)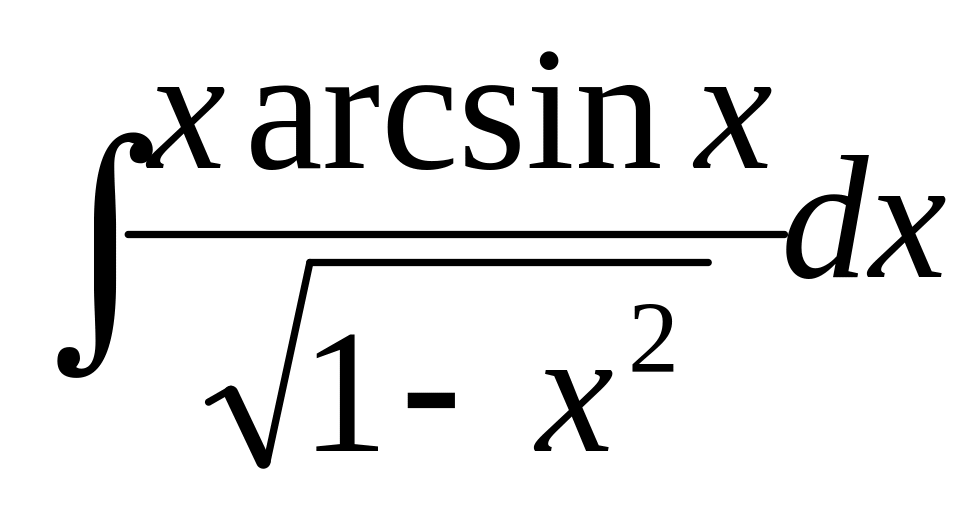 ,
в)
,
в)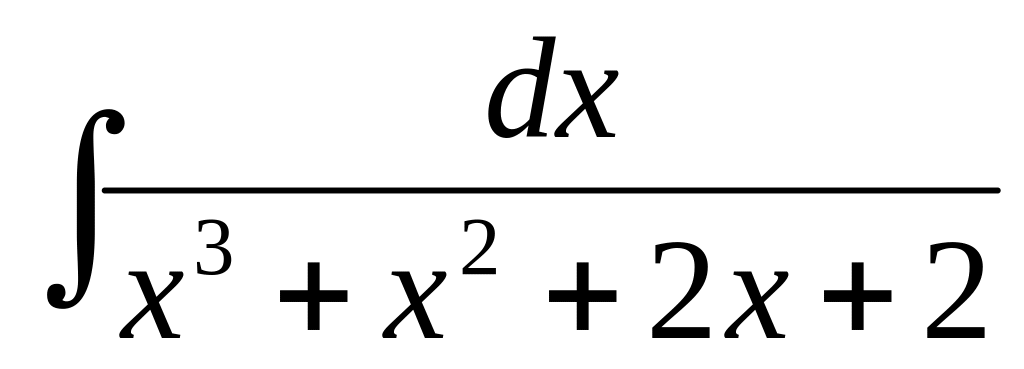 ,
г)
,
г)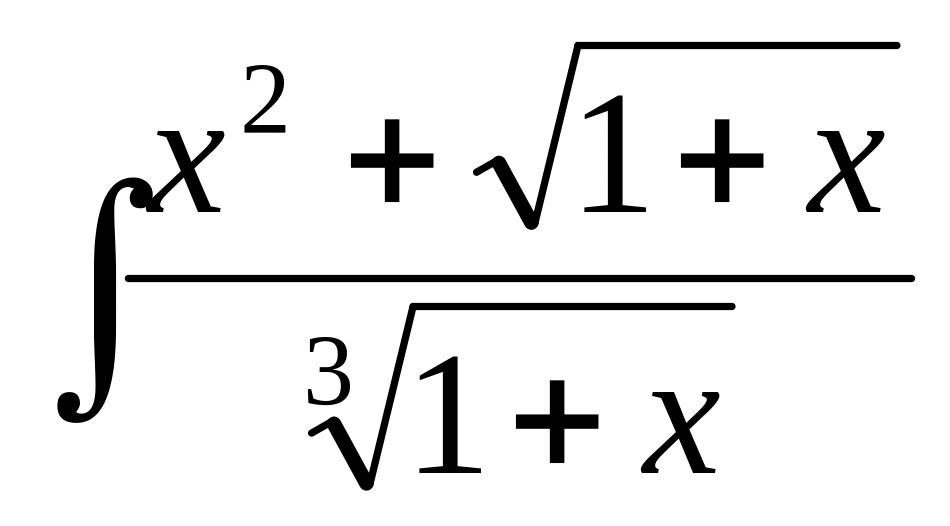 .
.а)
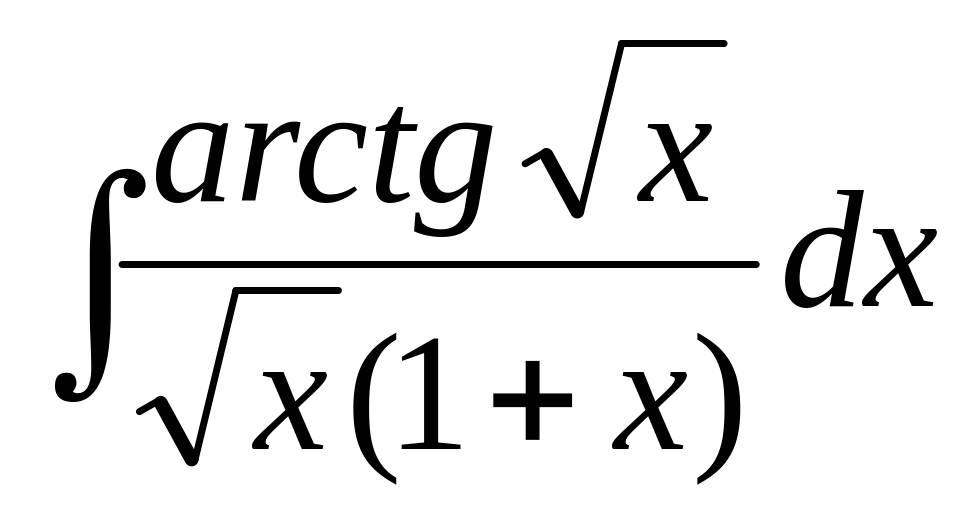 ,
б)
,
б)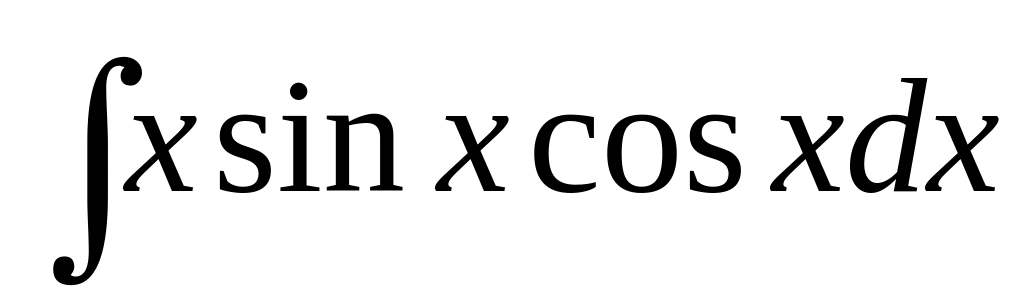 ,
в)
,
в)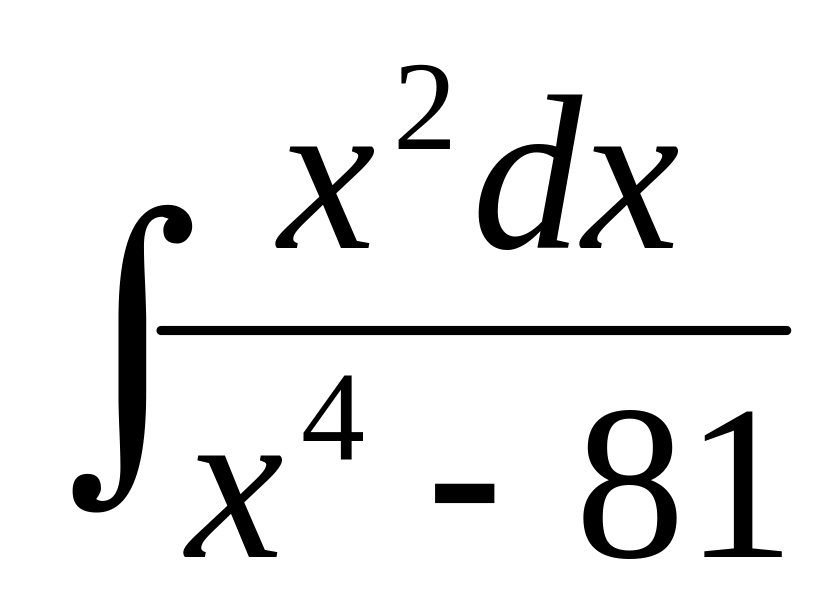 ,
г)
,
г)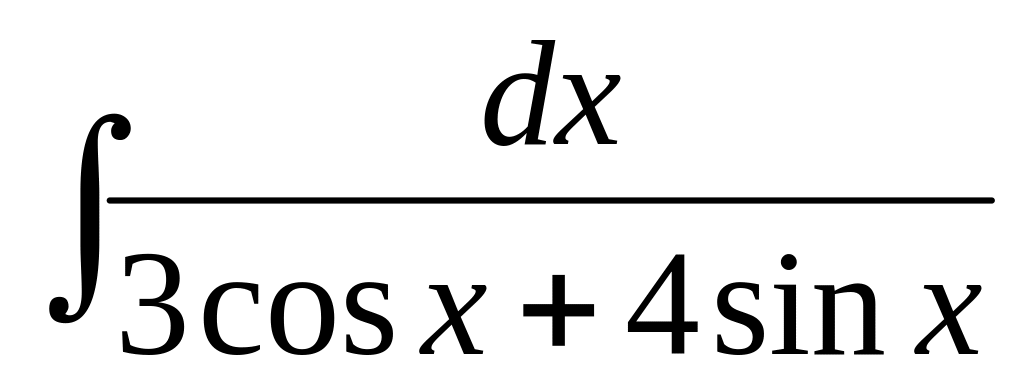 .
.а)
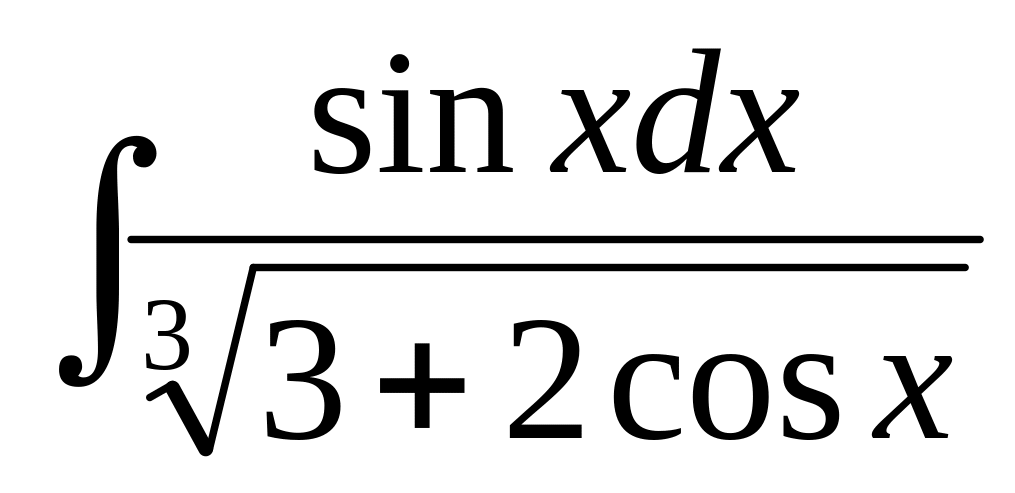 ,
б)
,
б)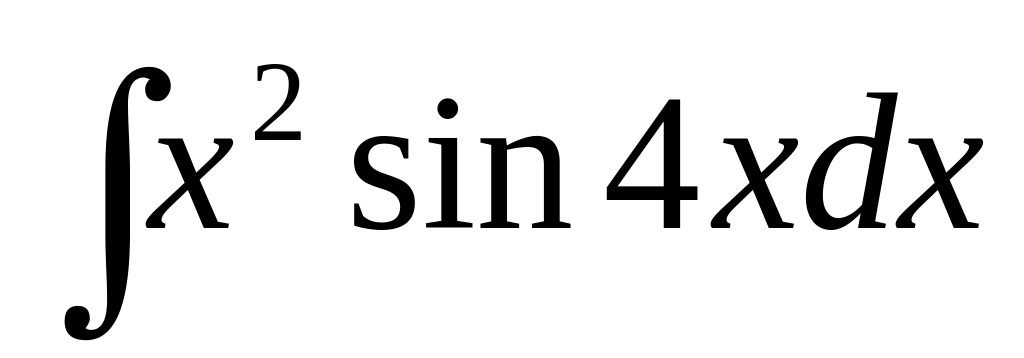 ,
в)
,
в) ,
г)
,
г)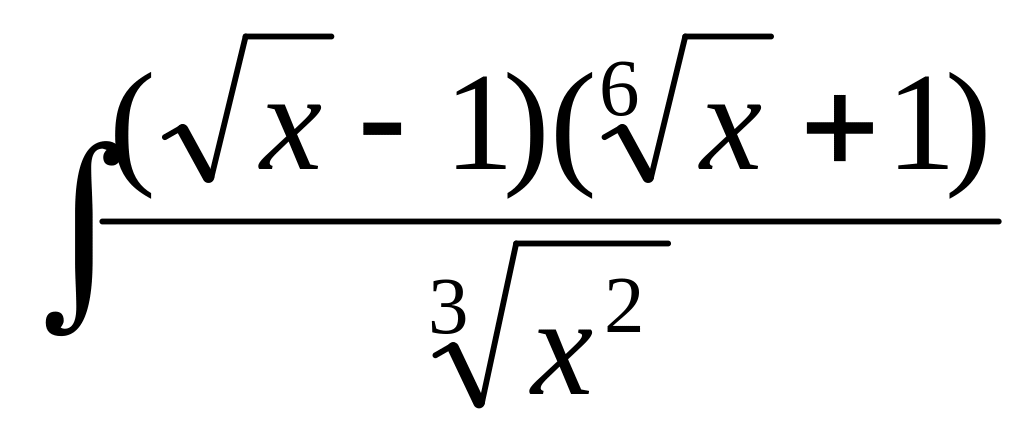 .
.а)
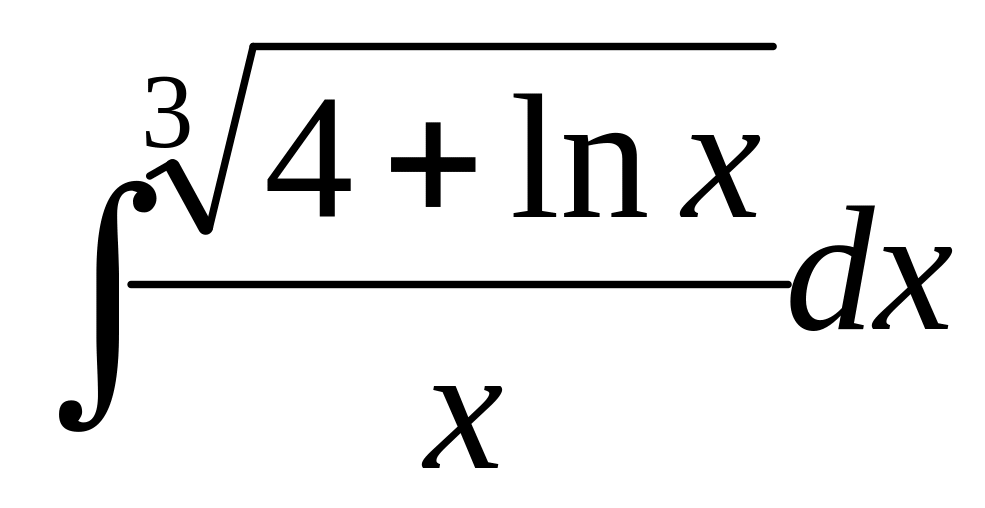 ,
б)
,
б)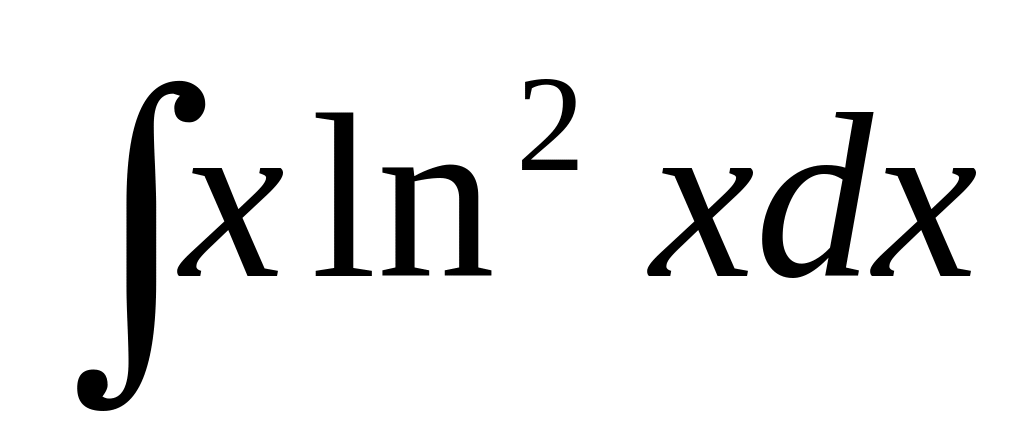 ,
в)
,
в)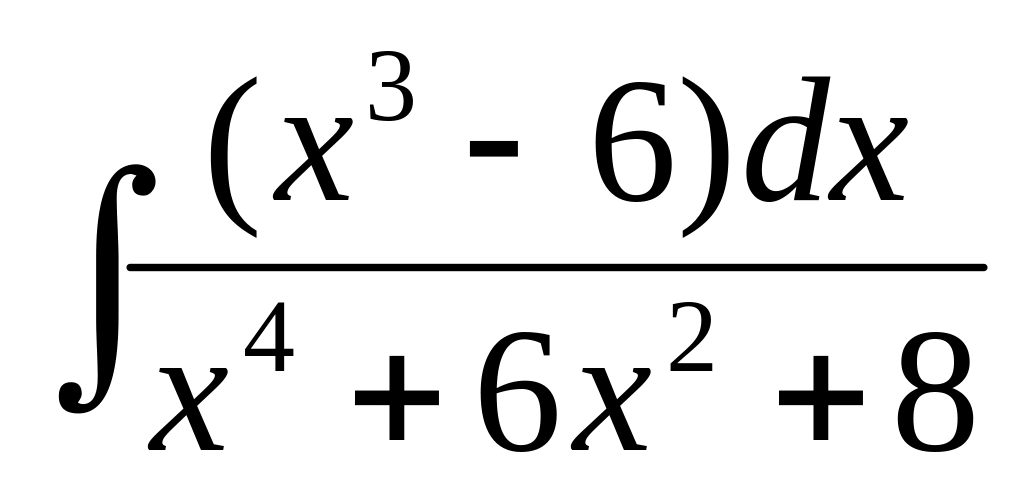 ,
г)
,
г)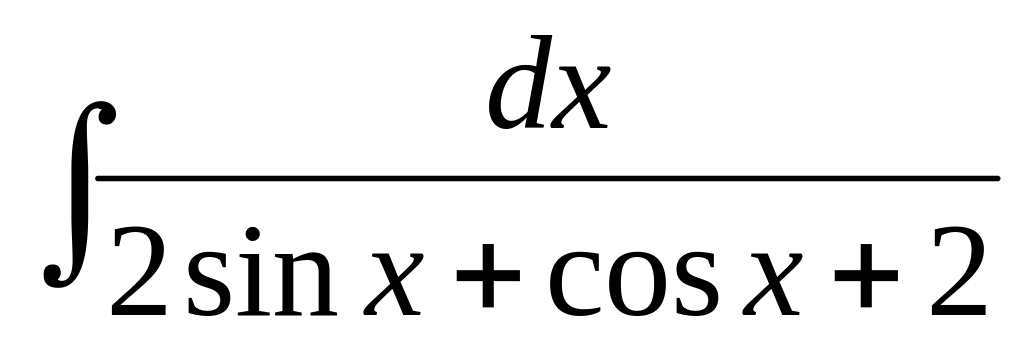 .
.
4. Вычислить несобственный интеграл или доказать его расходимость.
а)
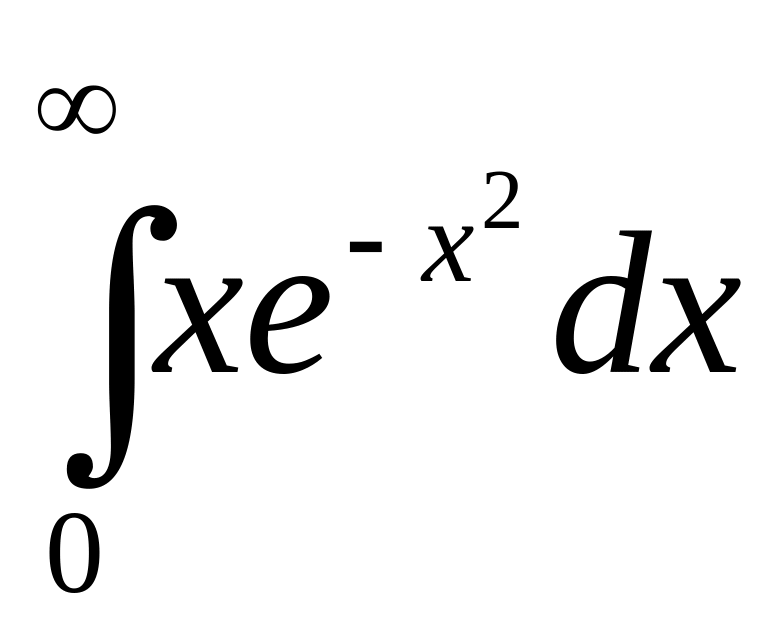 ;
;а)
 ;
;а)
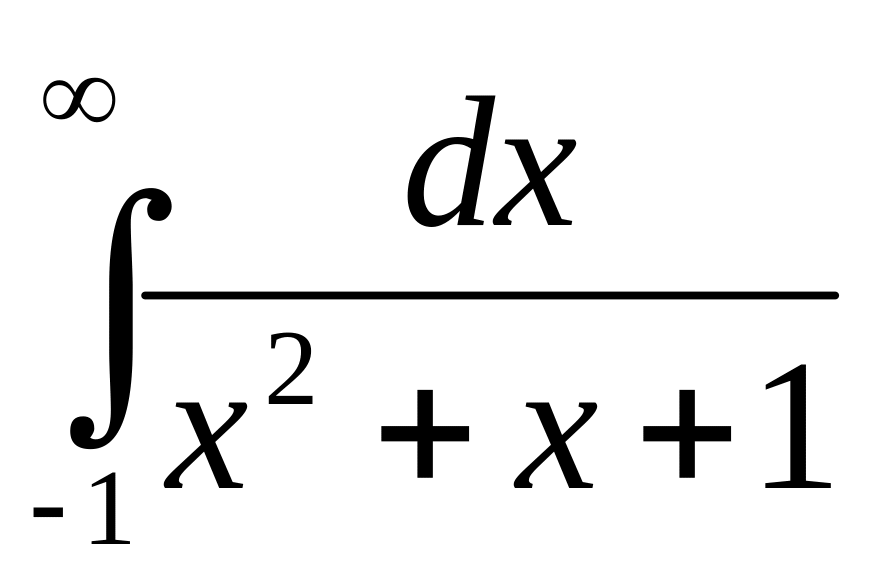 ;
;а)
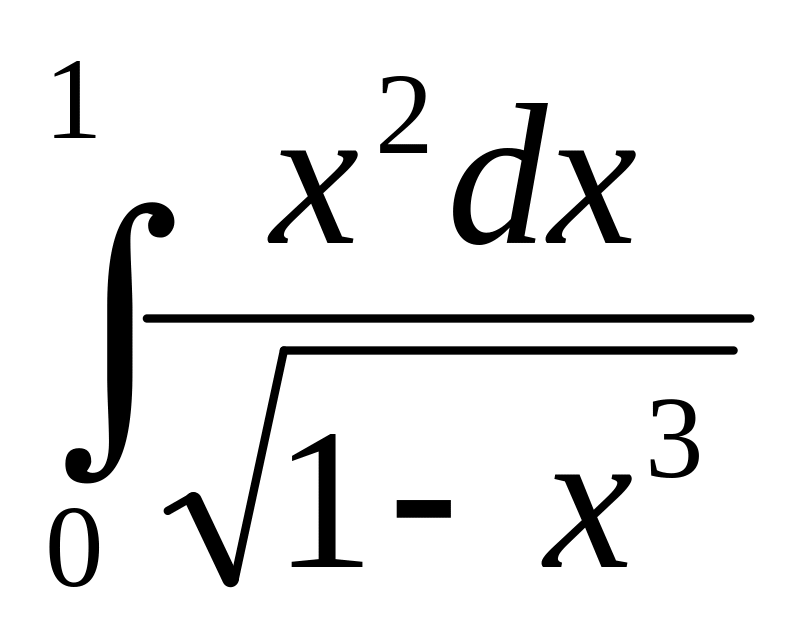 ;
;а)
 ;
;а)
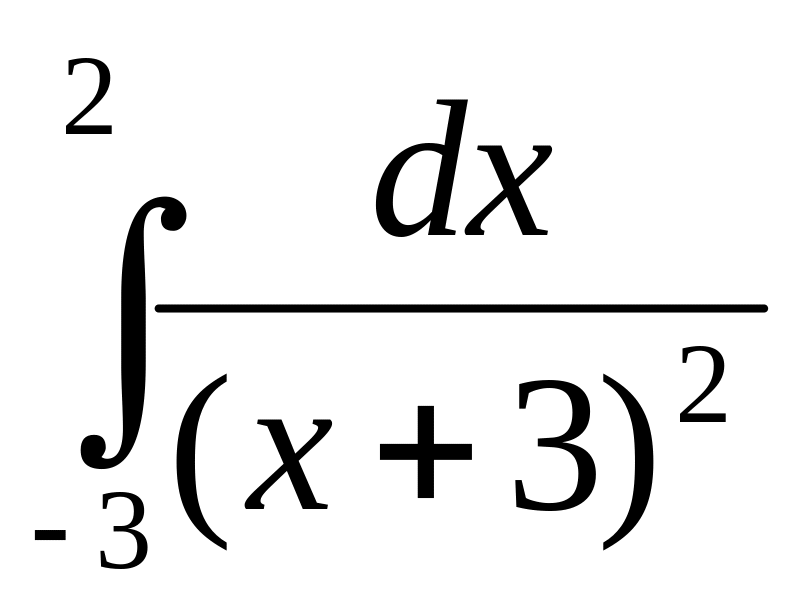 ;
;а)
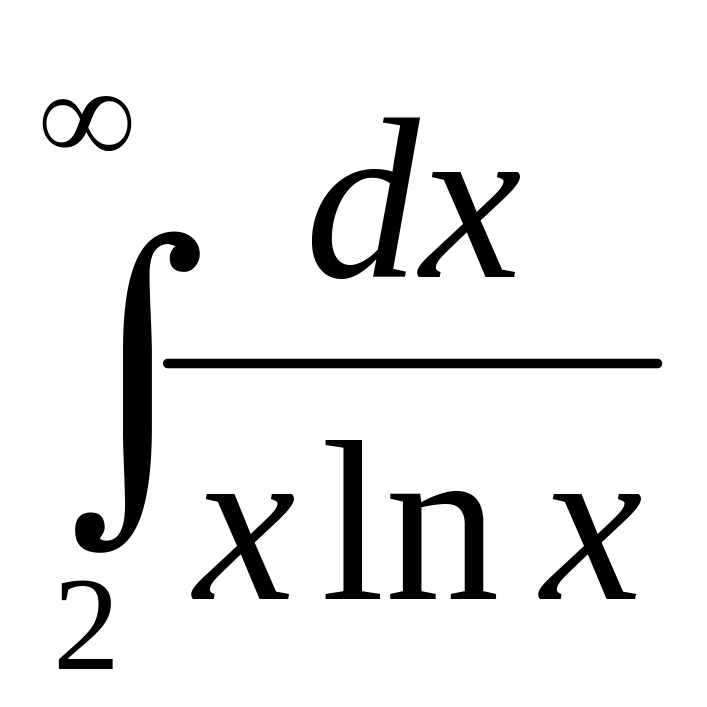 ;
;а)
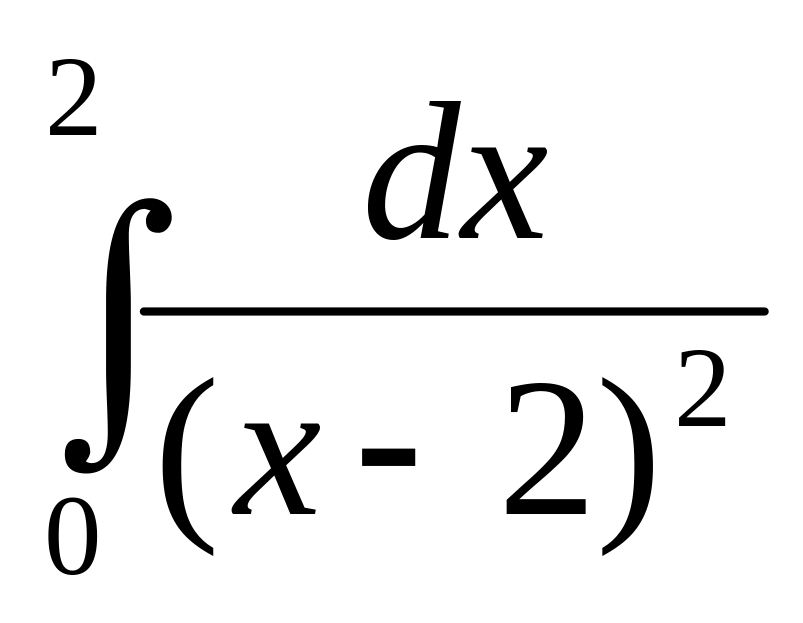 ;
;а)
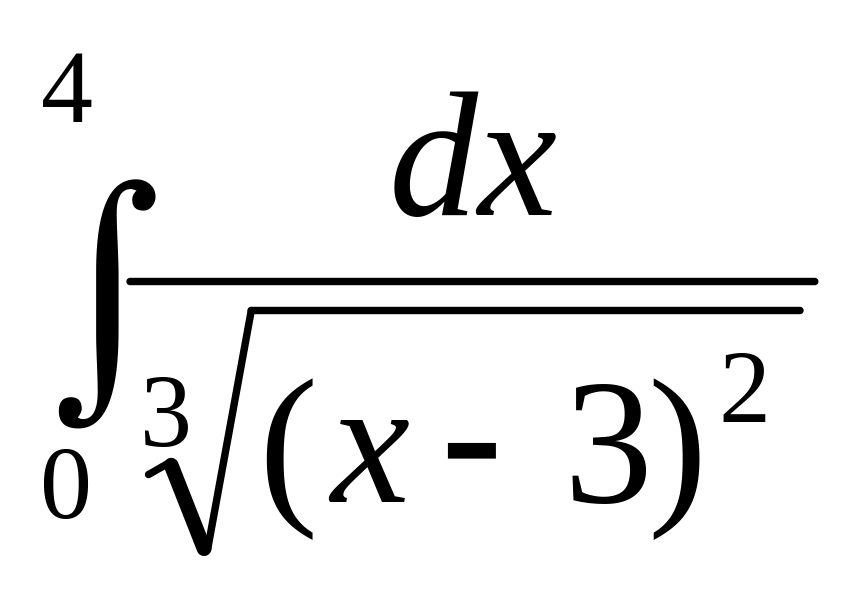 ;
;а)
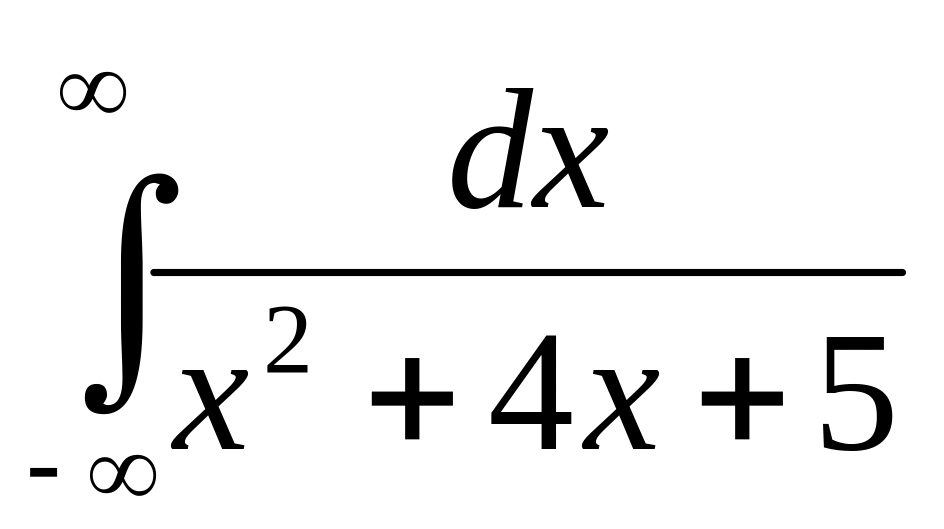 .
.
5. Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям.
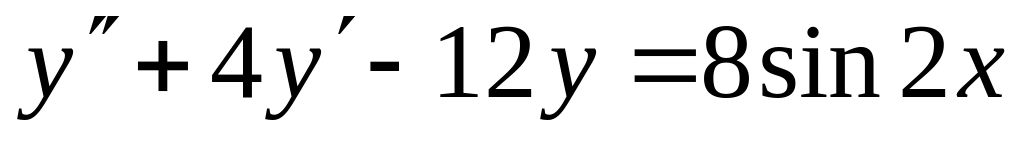 ,
, 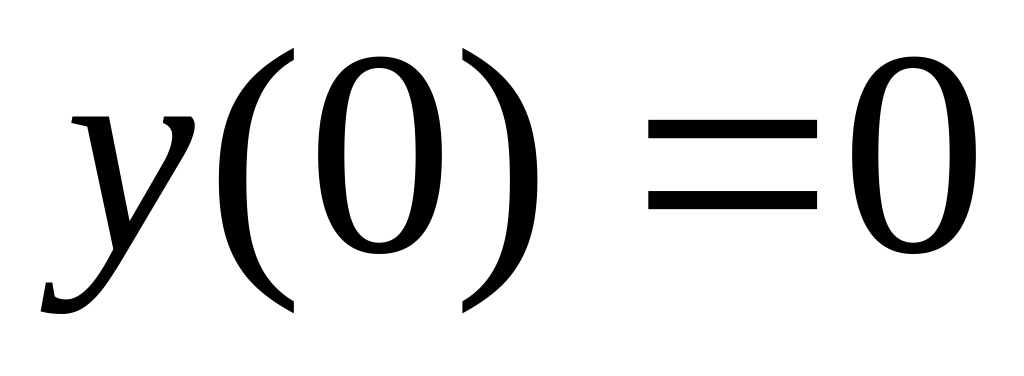 ,
, 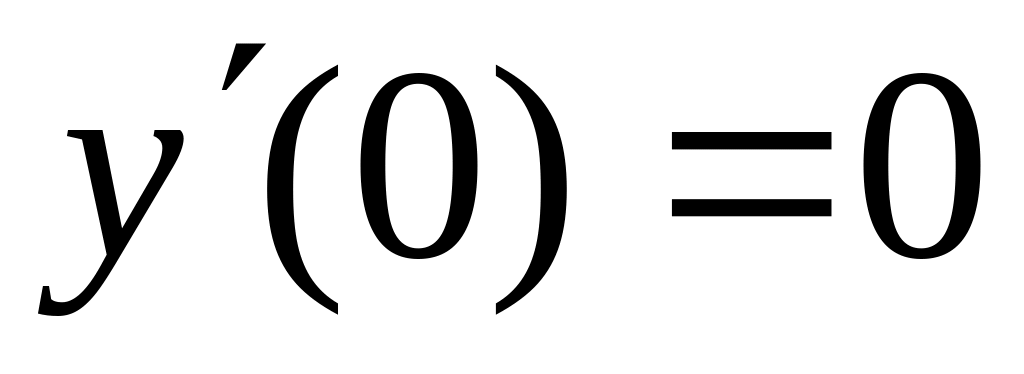 ;
;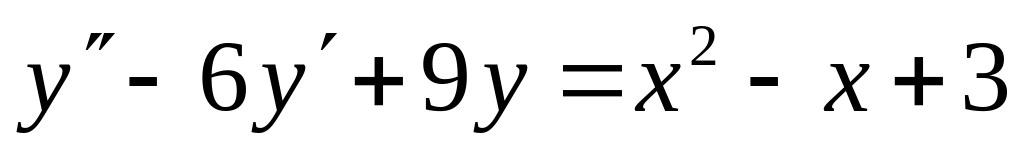 ,
, 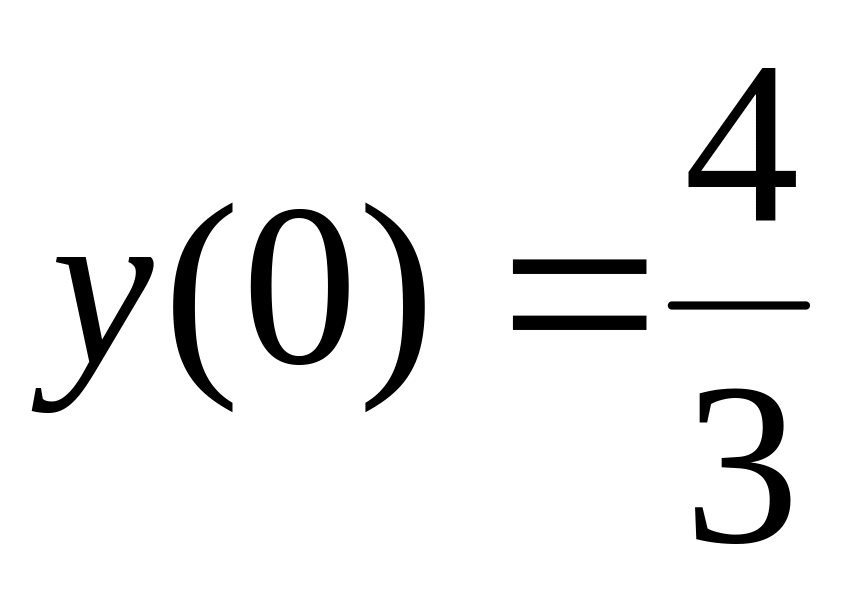 ,
, 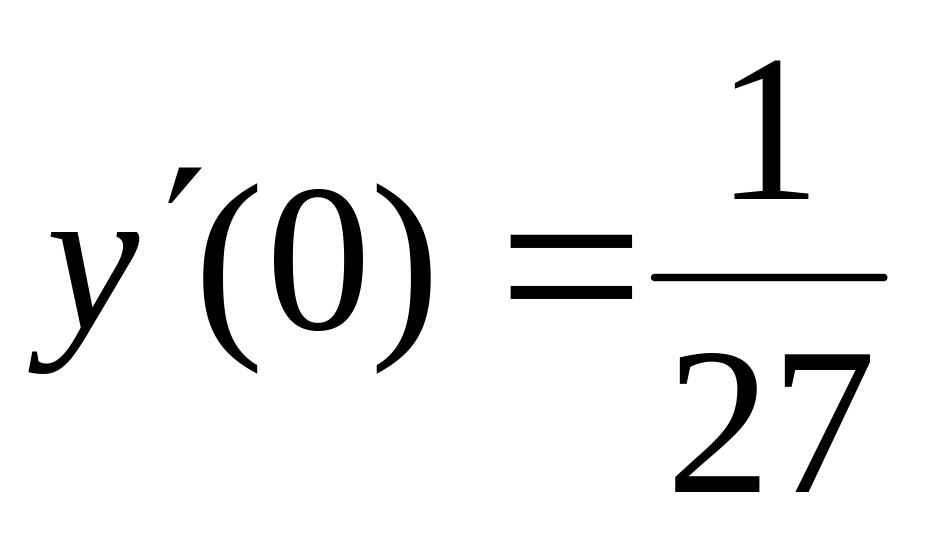 ;
;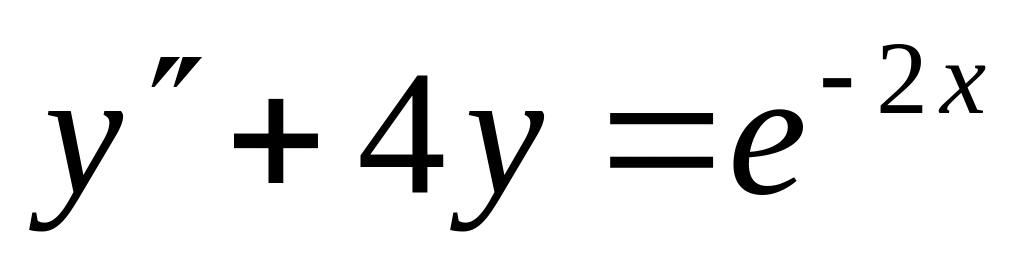 ,
,
;
,
,
;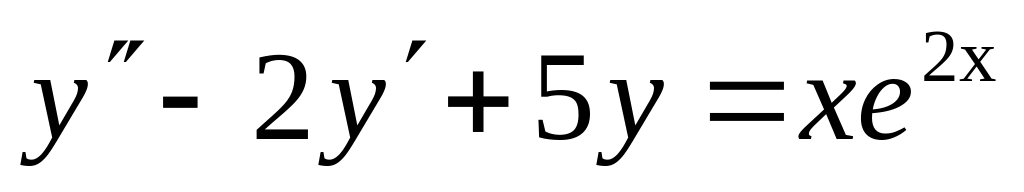 ,
, 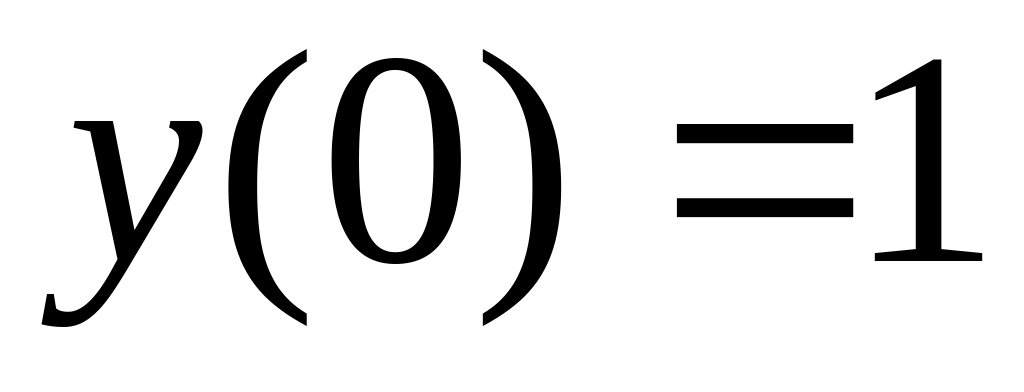 ,
;
,
;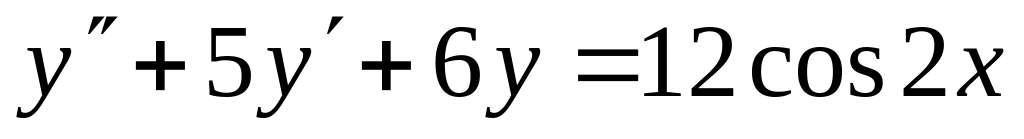 ,
,
,
, 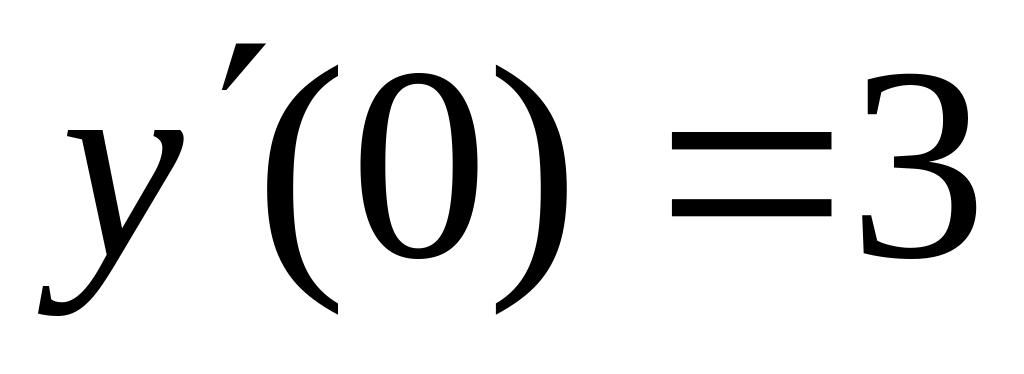 ;
;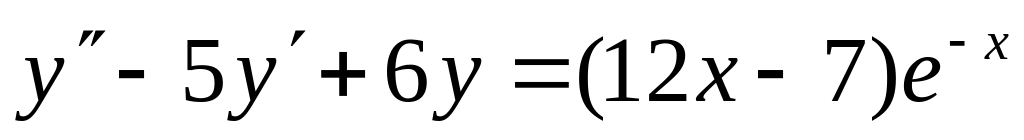 ,
,
;
,
,
;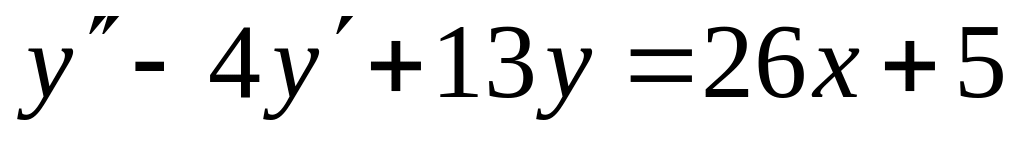 ,
,
;
,
,
;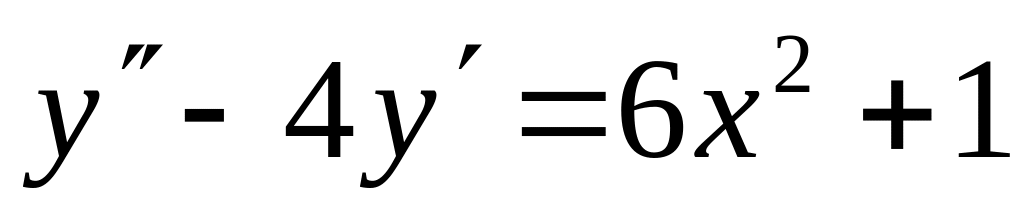 ,
, 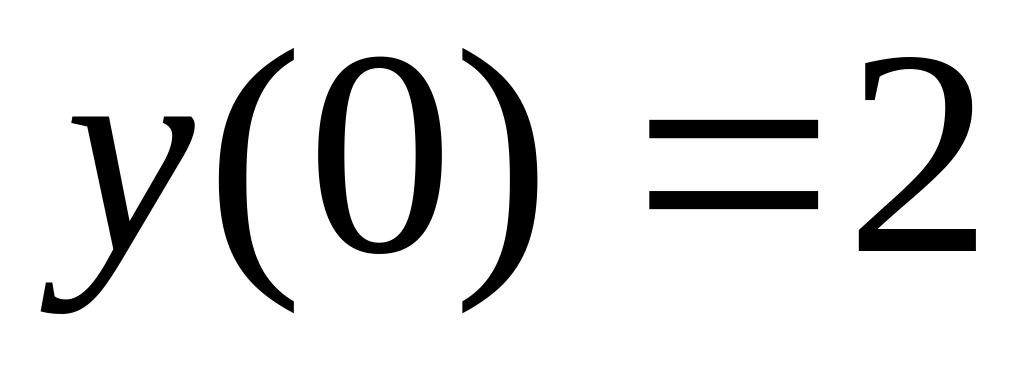 ,
;
,
;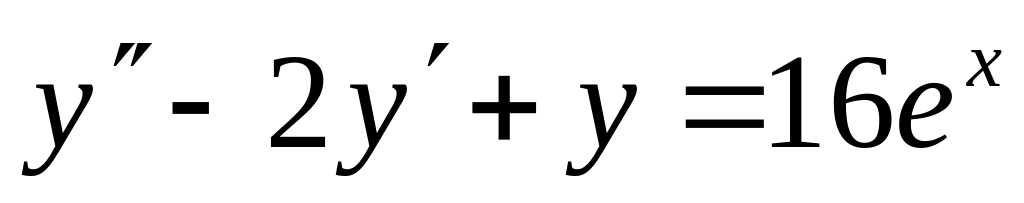 ,
,
,
,  ;
;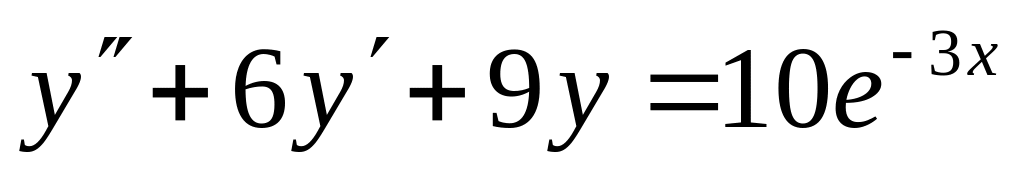 ,
,  ,
.
,
.
6. Найти радиус и интервал сходимости степенного ряда. Исследовать сходимость ряда на концах интервала сходимости.
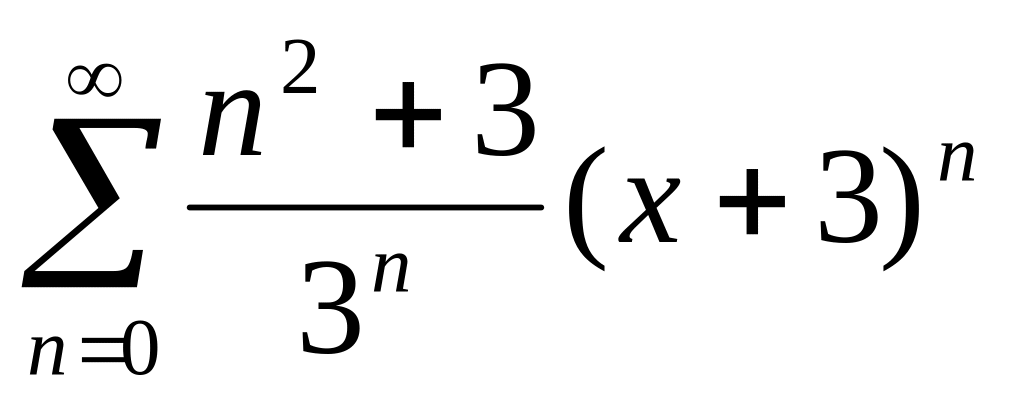 ,
, ,
,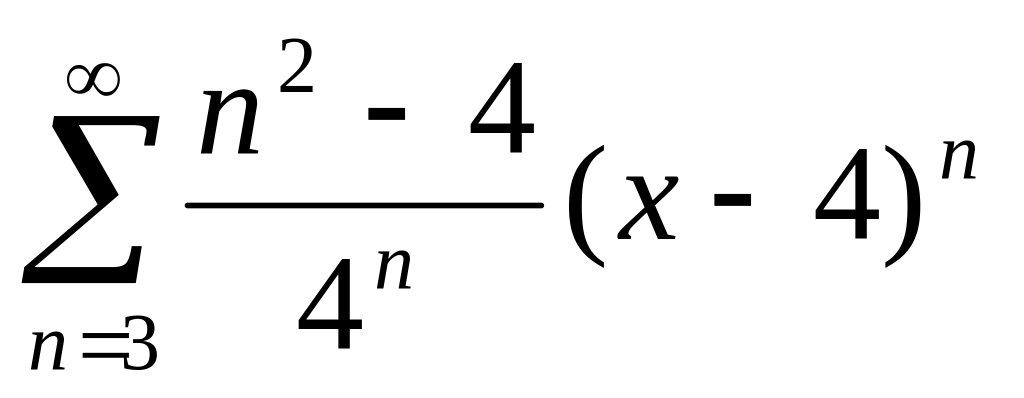 ,
,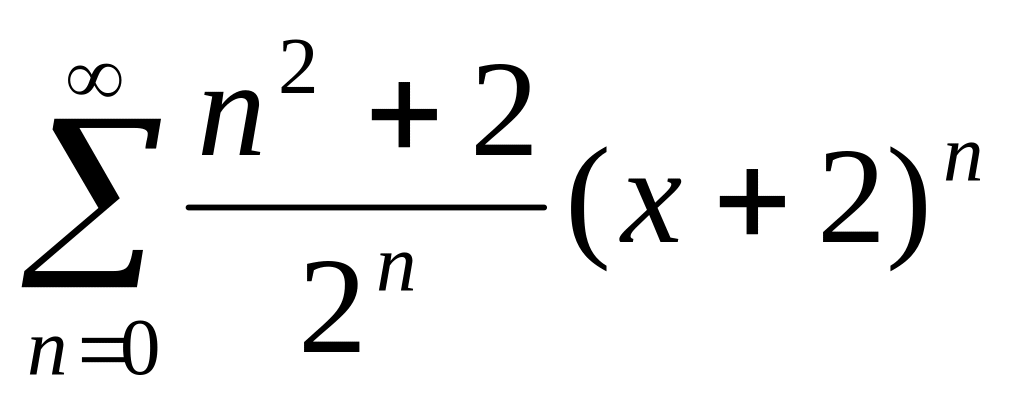 ,
,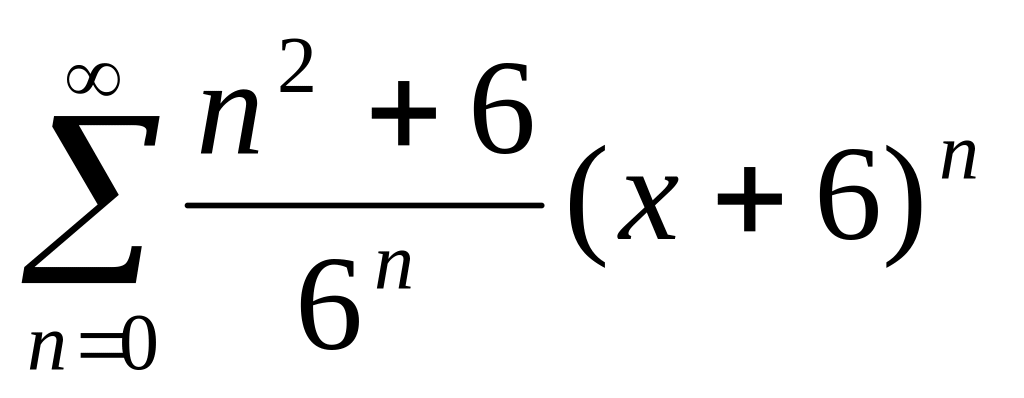 ,
,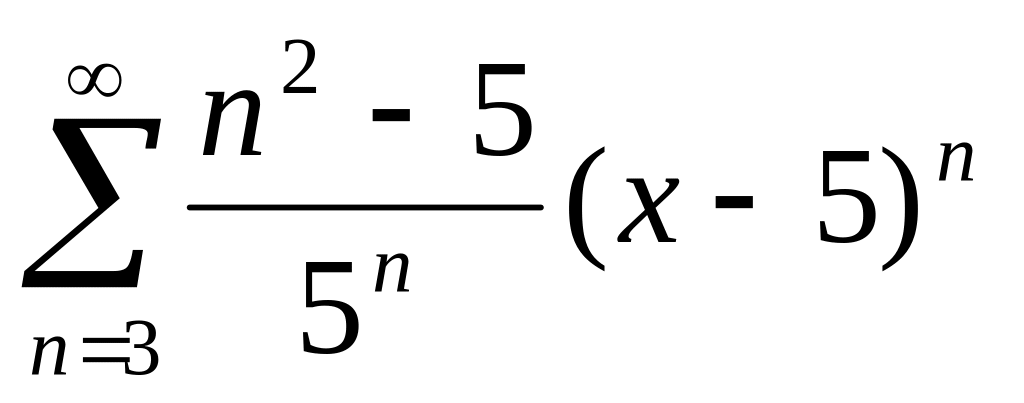 ,
,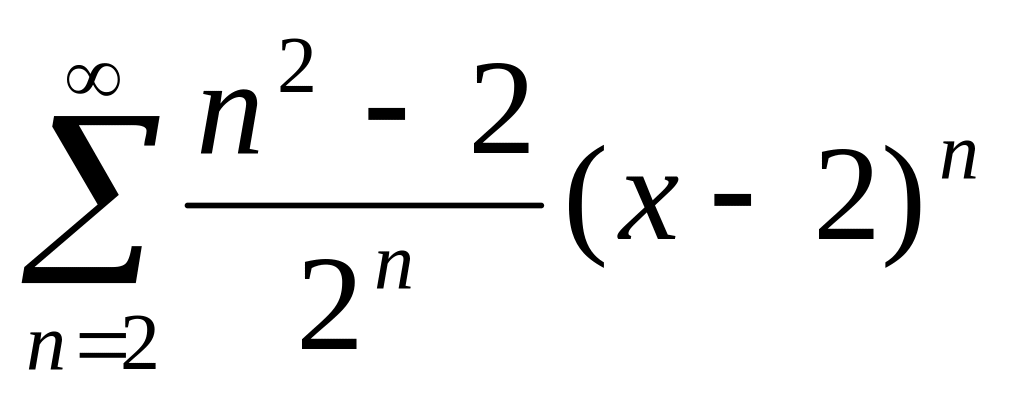 ,
,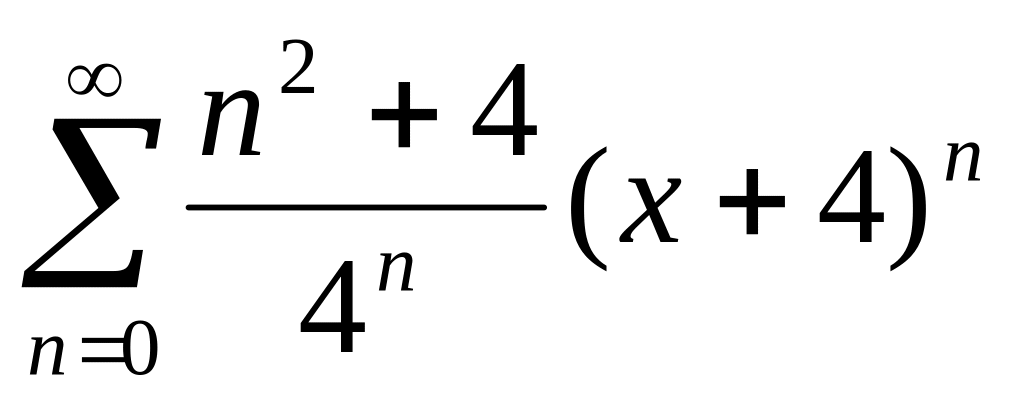 ,
, ,
,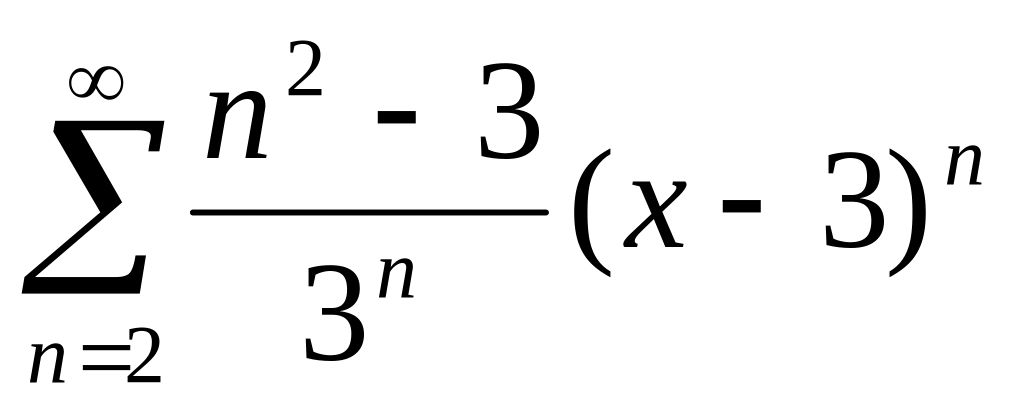 .
.
7. Решите задачу.
Студент знает 45 из 60 вопросов программы. Каждый экзаменационный билет содержит три вопроса. Найти вероятность того, что: а) студент знает все три вопроса; б) только два вопроса; в) только один вопрос экзаменационного билета.
В каждой из двух урн находятся 5 белых и 10 черных шаров. Из первой урны во вторую переложили наудачу один шар, а затем из второй урны вынули наугад один шар. Найти вероятность того, что вынутый шар окажется черным.
Три стрелка в одинаковых и независимых условиях произвели по одному выстрелу по одной и той же цели. Вероятность поражения цели первым стрелком равна 0.9, вторым – 0.8, третьим – 0.7. Найти вероятность того, что: а) только один из стрелков попадет в цель; б) только два стрелка попадут в цель; в) все три стрелка попадут в цель.
Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0.8. Найти вероятность того, что в 1600 испытаниях событие наступит 1200 раз.
Для сигнализации об аварии установлены три независимо работающих устройства. Вероятность того, что при аварии сработает первое устройство, равна 0.9, второе – 0.95 и третье – 0.85. Найти вероятность того, что при аварии сработает: а) только одно устройство; б) только два устройства; в) все три устройства.
Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0.02. Найти вероятность того, что в 150 испытаниях событие наступит 5 раз.
В партии из 1000 изделий имеются 10 дефектных. Найти вероятность того, что среди 50 изделий, наудачу взятых из этой партии, ровно 3 окажутся дефектными.
Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0.8. Найти вероятность того, что в 125 испытаниях событие наступит не менее 75 и не более 90 раз.
На трех станках при одинаковых и независимых условиях изготовляют детали одного наименования. На первом станке изготовляют 10%, на втором – 30%, на третьем – 60% всех деталей. Вероятность каждой детали быть бездефектной, равна 0.7 – если она изготовлена на первом станке, 0.8 – если на втором стенке, и 0.9 – если на третьем станке. Найти вероятность того, что взятая наугад деталь окажется бездефектной.
Два брата входят в состав двух спортивных команд, состоящих из 12 человек каждая. В двух урнах имеются по 12 билетов с номерами от 1 до 12. Члены каждой команды вынимают наудачу по одному билету из определенной урны (без возвращения). Найти вероятность того, что оба бората вытащат билет номер 6.
8. Решите задачу.
В экзаменационном билете 3 вопроса. Вероятность ответа на первый вопрос – 0,9; на второй – 0,7; на третий – 0,5. Вопросы равноценны. Найти вероятности различных оценок.
На трех станках производятся одинаковые изделия. На первом станке производится 40% продукции высшего сорта. На втором – 50%, на третьем – 80%. Наудачу взято по одному изделию из продукции каждого станка. Найти вероятность того, что: 1) все три изделия оказались высшего сорта; 2) два изделия из трех высшего сорта; 3) только одно изделие из трех высшего сорта; 4) хотя бы одно изделие из трех высшего сорта.
Три автомата фасуют пельмени. За смену первый автомат выпускает 30000 коробок пельменей, из них с браком 900 штук; второй – 20000 и 500 с браком; третий - 10000 и 400 с браком. Из продукции каждого автомата берётся по одной коробке. Найти вероятность того, что: 1) все три коробки без брака; 1) две коробки из трёх без брака; 3) только одна из трёх коробок без брака; 4) хотя бы одна коробка без брака.
Три завода поставляют компьютеры. Не требуют гарантийного ремонта 80% компьютеров первого завода, 75% - второго завода и 85% - третьего. Куплено по одному компьютеру каждого завода. Найти вероятность того, что не потребуют гарантийного ремонта: 1) все три компьютера; 2) два компьютера из трёх; 3) только один компьютер из трех; 4) хотя бы один компьютер из трех не потребует гарантийного ремонта.
Три предприятия выпускают одинаковую продукцию в пропорции 3:1:2. Всего изготовлено 6000 изделий, причем на первом предприятии изделий высшего сорта выпускается 2000, на втором – 8000 и на третьем – 1500. Наудачу берется по одному изделию из продукции каждого предприятия. Найти вероятность того, что: 1) все три изделия высшего сорта; 2) два изделия из трех высшего сорта; 3) только одно изделие из трех высшего сорта; 4) хотя бы одно изделие из трех высшего сорта.
В двух партиях одинаковых изделий по 10 и 15 штук находится по две бракованных детали. Все детали поступили в сборочный цех. 1) Найти вероятность того, что взятое изделие годное.2) На сборку взята годная деталь. Какова вероятность того, что она из второй партии? 3) На сборку взята бракованная деталь. Какова вероятность того, что она из первой партии?
В цехе три группы станков-автоматов производят одни и те же детали. Станки первой группы производят 70% деталей первого сорта, второй – 65 % и третьей – 80%. В первой группе 5 станков, во второй – 9 и в третьей –2. 1) Найти вероятность того, что взятая наудачу деталь будет первого сорта. 2) Деталь оказалась первого сорта. Найти вероятность того, что она изготовлена на первой группе станков. 3) Деталь оказалась нестандартной. Какова вероятность того, что она изготовлена на третьей группе станков?
Три предприятия выпускают одинаковую продукцию в пропорции 2:2:1. Доля брака на первом предприятии составляет 10 %, на втором – 15%, на третьем – 5%. Продукция поступает на склад. Со склада взято одно изделие. Найти вероятность того, что: 1) Взятое изделие оказалось не бракованным. 2) Взятое изделие оказалось не бракованным. Какова вероятность, что оно изготовлено на первом предприятии? 3) Взятое изделие оказалось бракованным. Какова вероятность того, что оно сделано на втором предприятии?
Три завода поставляют телевизоры в пропорции 1:2:3. Не требуют гарантийного ремонта 70% телевизоров первого завода, 75% - второго завода и 80% - третьего. В магазине куплен телевизор. 1) Найти вероятность того, что он не потребует гарантийного ремонта. 2) Купленный телевизор проработал без гарантийного ремонта. Найти вероятность того, что его поставил второй завод. 3) Купленный телевизор потребовал ремонта в гарантийный срок. Найти вероятность того, что он поставлен третьим заводом.
На склад завода поступили компьютеры трех партий. Известно, что в 1-й партии, состоящей из 14 штук, 2 компьютера нестандартных, во 2-ой, состоящей из 12 штук, тоже 2 компьютера нестандартных и в 3-й, состоящей из 18 штук, - 3 нестандартных. 1) Найти вероятность того, что купленный компьютер будет стандартным. 2) Купленный компьютер оказался стандартным. Какова вероятность того, что он из 2-й партии? 3) Купленный компьютер оказался нестандартным. Какова вероятность того, что он из первой партии?
9. В магазин поступили однотипные изделия из трех заводов, причем i – тый завод поставляет mi % изделий. Среди изделий i – го завода ni % первосортных. Куплено одно изделие. Оно оказалось первосортное. Определить вероятность того, что купленное изделие выпущено j – м заводом.
№ |
81 |
82 |
83 |
84 |
85 |
86 |
87 |
88 |
89 |
90 |
m1 |
50 |
50 |
50 |
60 |
60 |
60 |
40 |
40 |
40 |
40 |
m2 |
30 |
30 |
30 |
20 |
20 |
20 |
30 |
30 |
30 |
20 |
m3 |
20 |
20 |
20 |
20 |
20 |
20 |
30 |
30 |
30 |
40 |
n1 |
70 |
70 |
70 |
70 |
70 |
70 |
80 |
80 |
80 |
90 |
n2 |
80 |
80 |
80 |
80 |
80 |
80 |
80 |
80 |
80 |
90 |
n3 |
90 |
90 |
90 |
90 |
90 |
90 |
90 |
90 |
90 |
80 |
j |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
10. Решите задачу.
а) Вероятность «сбоя» в работе телефонной станции равна p. Поступили тысяча вызовов. Определить вероятность семи «сбоев».
№ |
91 |
92 |
93 |
94 |
95 |
96 |
97 |
98 |
99 |
100 |
p |
0,002 |
0,003 |
0,004 |
0,005 |
0,006 |
0,007 |
0,008 |
0,009 |
0,01 |
0,011 |
б) Вероятность наступления некоторого события в каждом из ста независимых испытаний равна p. Определить вероятность того, что число m наступлений события удовлетворяет неравенству к1 ≤ m ≤ к2.
№ |
91 |
92 |
93 |
94 |
95 |
96 |
97 |
98 |
99 |
100 |
||||||||
p |
0,8 |
0,8 |
0,8 |
0,7 |
0,7 |
0,7 |
0,7 |
0,6 |
0,75 |
0,75 |
||||||||
к1 |
80 |
85 |
70 |
85 |
50 |
65 |
70 |
40 |
65 |
70 |
||||||||
к2 |
90 |
95 |
95 |
95 |
60 |
75 |
80 |
50 |
80 |
85 |
||||||||
11. Случайная величина
![]() задана функцией распределения
задана функцией распределения
![]() .
Найти плотность распределения
вероятностей, математическое ожидание
и дисперсию случайной величины.
.
Найти плотность распределения
вероятностей, математическое ожидание
и дисперсию случайной величины.
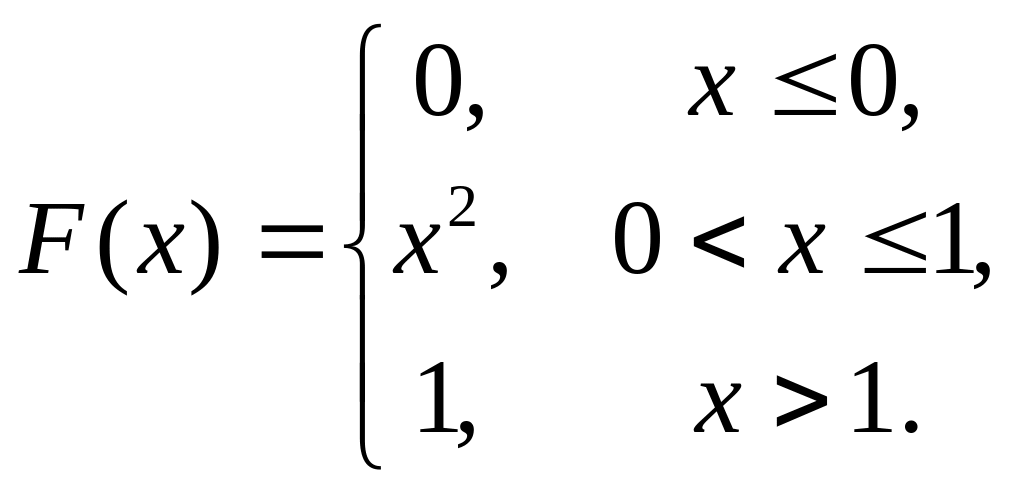
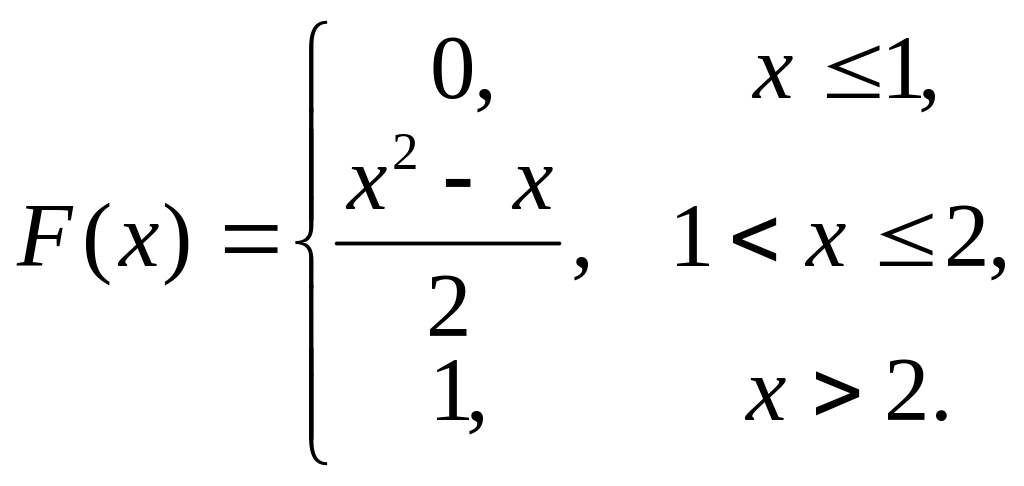
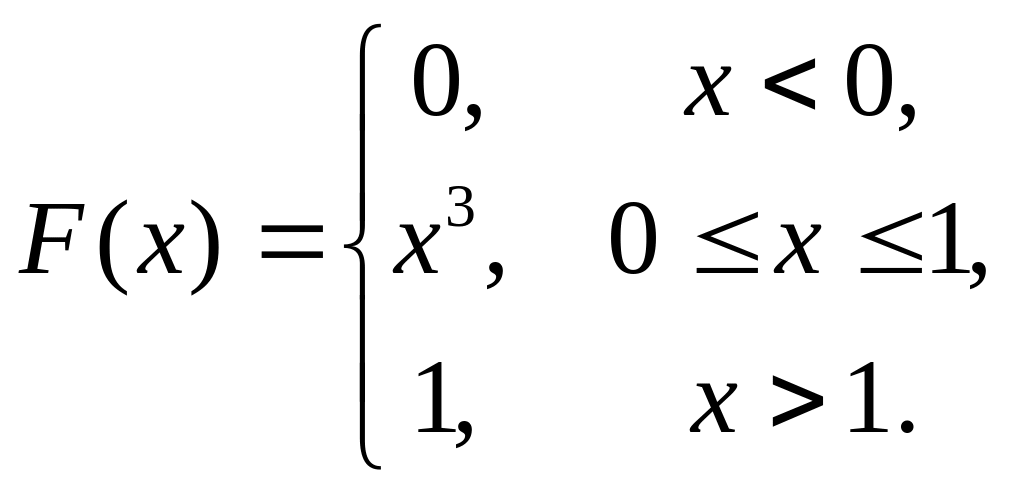
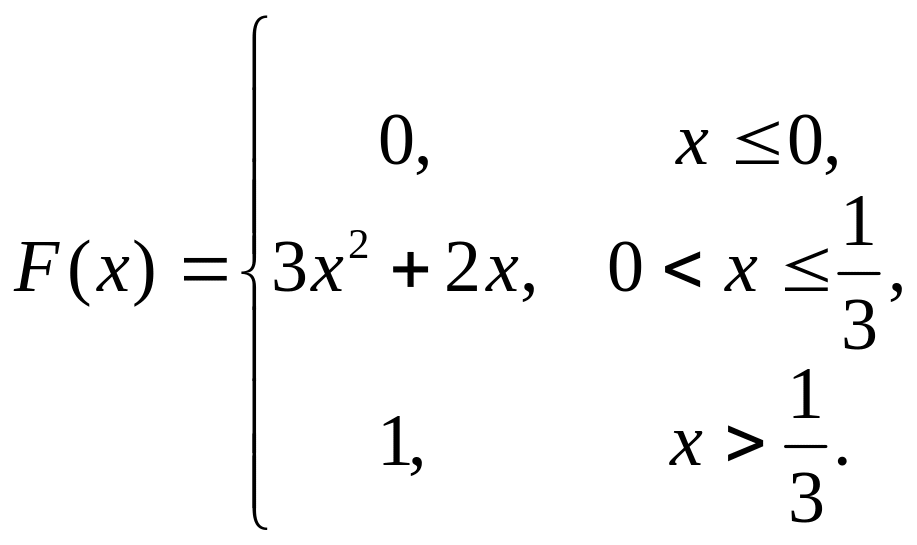
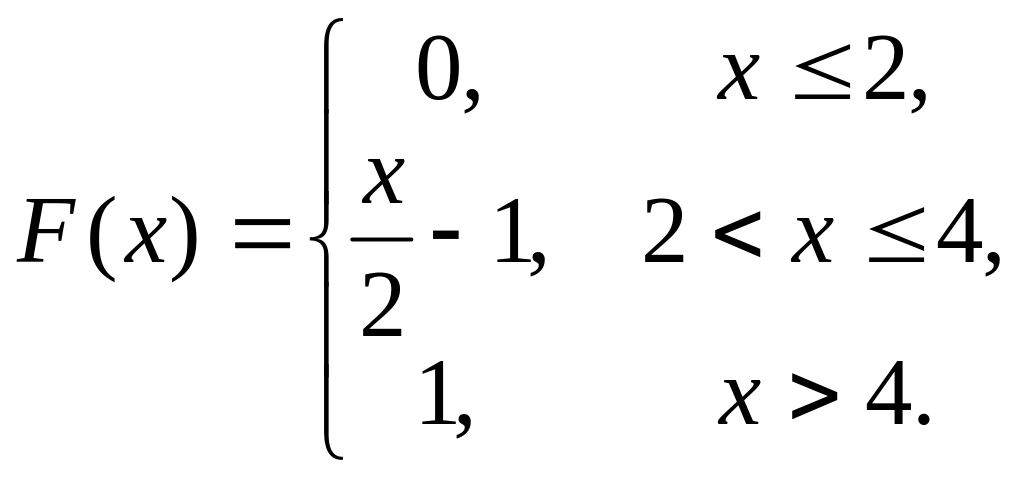
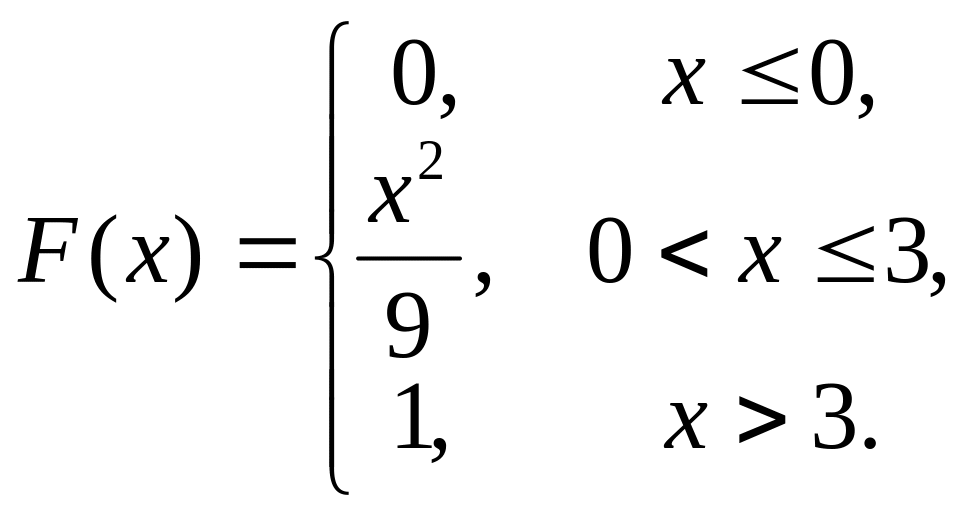
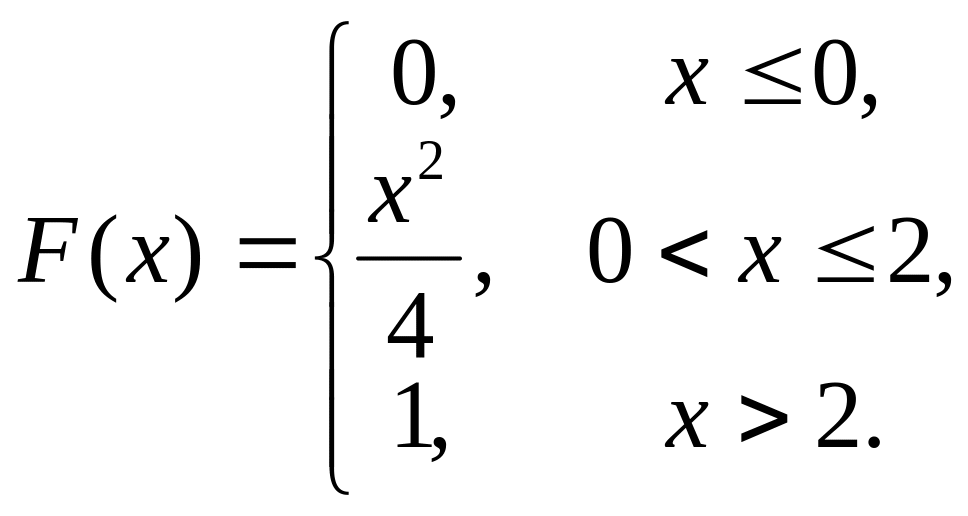

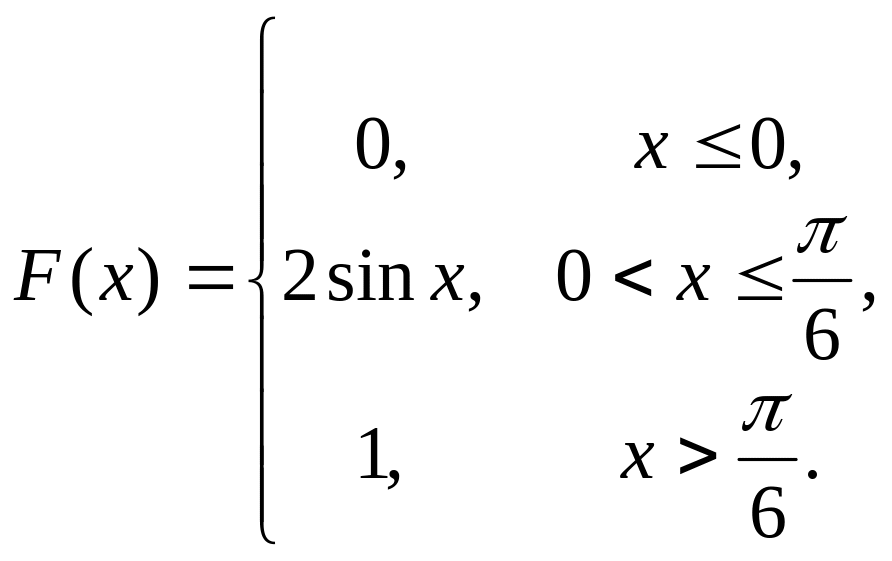
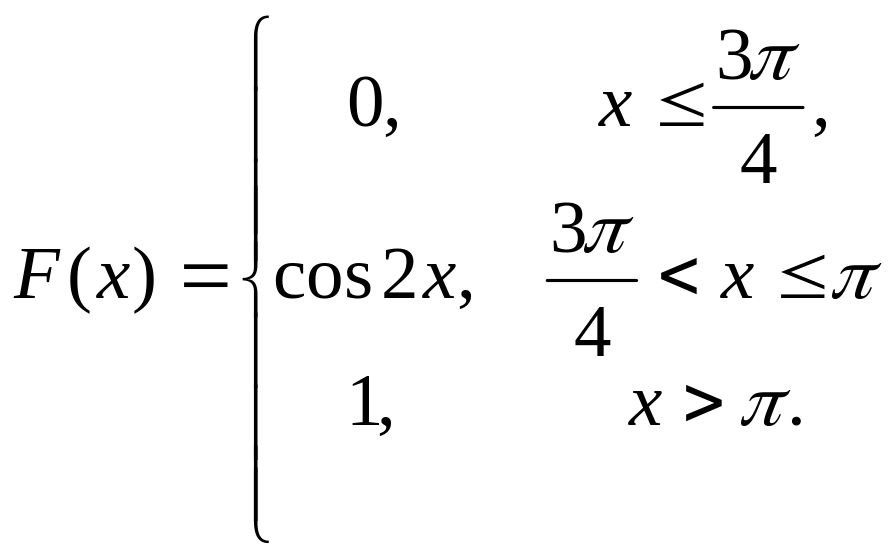 .
.
Требования к оформлению контрольной работы
При выполнении контрольных работ необходимо придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для переработки.
Каждая контрольная работа должна быть выполнена в отдельной тетради в клеточку чернилами любого цвета, кроме красного. Необходимо оставлять поля для замечаний рецензента.
В заголовке работы на обложке тетради должны быть ясно написаны фамилия студента, его инициалы, здесь же следует указать название учебного заведения и группы, номер зачетной книжки, номер контрольной работы, название дисциплины. В конце работы поставить дату ее выполнения, расписаться.
В работу должны быть включены все задачи, указанные в задании строго по положенному варианту. Решения задач надо располагать в порядке номеров, указанных в заданиях, сохраняя номера задач. Перед решением каждой задачи надо полностью выписать его условие. В том случае, если несколько задач, из которых студент выбирает задачи своего варианта, имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные, взятыми из соответствующего номера. Решение задач следует излагать подробно и аккуратно, мотивируя все действия по ходу решения и делая необходимые чертежи.
Контрольные работы, содержащие не все задания, а также задачи не своего варианта, не зачитываются.
После получения прорецензированной работы, как не зачтенной, так и зачтенной, студент должен исправить все отмеченные рецензентом ошибки и недочеты и выполнить все его рекомендации.
Если контрольная работа зачтена и выполнены исправления с учетом замечаний рецензента, то студенту назначается время защиты контрольной работы во время экзаменационной сессии. Без предъявления отрецензированных контрольных работ студент не допускается к зачету.
Вопросы к экзамену.
(Конспект можно писать по темам (12))
1. Введение в математический анализ
§1. Множества
§2. Операции над множествами
§3. Последовательности
§4. Монотонные последовательности
§5. Понятие функции
§6. Пределы функции
§7. Бесконечно большие и бесконечно малые функции
§8. Первый замечательный предел
§9 Сравнение бесконечно малых функций
§10 Непрерывность функции
§11 Точки разрыва функции
2. Производная и дифференциал функции
§1. Определение производной
§2.Непрерывность и дифференцируемость функции
§3. Правила дифференцирования
§4. Формулы дифференцирования элементарных функций
§5. Примеры отыскания производных сложных функций
§6. Дифференцирование неявных функций
§7. Дифференцирование функций, заданных параметрически
§8. Логарифмическое дифференцирование
§9. Производные высших порядков
§10. Производные высших порядков от неявных функций и от функций, заданных параметрически
§11. Дифференциал функции
§12. Дифференциалы высших порядков
3. Применение производных к исследованию свойств функции
§1. Возрастание и убывание функций; экстремум функции
§2. Теоремы Ферма, Ролля, Лагранжа и Коши
§3. Правило Бернулли-Лопиталя для раскрытия неопределенностей
§4. Формула Тейлора
§5. Признаки возрастания, убывания и экстремума функции
§6. Наибольшее и наименьшее значения функции на данном отрезке
§7. Выпуклость и вогнутость графика функции; точки перегиба
§8. Асимптоты графика функции
§9. Построение графика функции
