10.5. Различные методы достижения точности сборки

Задачи, связанные с достижением требуемой точности машин и их механизмов на всех этапах их создания (проектирова­ние, изготовление, сборка), решаются с помощью размерных и кинематических цепей (см. «Методические указания. Цепи раз­мерные. Основные понятия. Методы расчета линейных и угловых цепей. РД 50-635-87»).

В зависимости от типа производства различают пять методов достижения точности замыкающего звена при сборке: 1) полной взаимозаменяемости; 2) неполной (частичной) взаимозаменяемости; 3) групповой взаимозаменяемости; 4) регулировки; 5) пригонки.

В основном применяют первых два метода, обеспечивающих взаимозаменяемость при сборке с наименьшими затрачами труда.

Метод полной взаимозаменяемости

Его сущность заключается в том, что требуемая точность замыкающего звена размерной цепи достигается у всех объектов путем включения в нее составляющих звеньев без выбора, под­бора или изменения их величин.

Метод полной взаимозаменяемости экономично применять в условиях достижения высокой точности при малом числе звеньев

размерной цепи в крупносерийном и массовом производстве. Основан этот метод на расчете размерных цепей на максимум-минимум. Метод прост и обеспечивает 100%-ную взаимозаменяе­мость, но имеет существенный недостаток — уменьшает допуски на составляющие звенья (что приводит к увеличению трудоем­кости и себестоимости их изготовления), т. е. основывается на расчете по крайним предельным отклонениям размеров цепи при неблагоприятном их сочетании (например, вал изготовлен с ми­нимальным диаметром, а втулка, соединяемая с ним, — с макси­мальным).

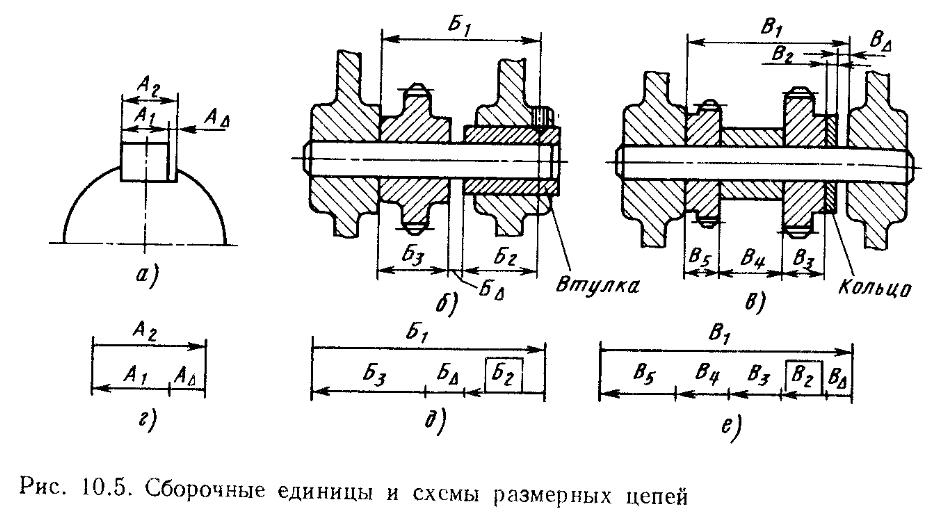
На рис. 10.5 приведены сборочные единицы (рис. 10.5, а, б, в) и схемы размерных цепей (рис. 10.5, г, д, е).

Размерной цепью называют совокупность размеров, непосред­ственно участвующих в решении поставленной задачи и образую­щих замкнутый контур. Размеры обозначают прописными бук­вами русского (А, Б, В, Г и т. д.) или строчными греческого алфавитов.

Размеры, входящие в цепь, называются звеньями размерной цепи. Различают: замыкающие звенья (звенья, получаемые при сборке последними или являющиеся исходными при постановке задачи); составляющие звенья (увеличивающие и уменьшающие, с увеличением которых замыкающее звено увеличивается или уменьшается); компенсирующее звено, изменением которого до­стигается требуемая точность замыкающего звена).

Обозначения звеньев те же, что и размеров (А, Б, В и т. д.), но с добавлением индексов: А — для замыкающего звена, i — порядковый номер составляющего звена с обязательным указа­нием стрелкой: слева направо — для увеличивающего звена (-*-) и справа налево — для уменьшающего звена (ч-); для компенси­рующего звена букву заключают в прямоугольник.

При решении размерных цепей на максимум-минимум возни­кают прямая и обратная задачи. Прямая задача заключается в том, что конструктор в сборочной единице задает замыкающее звено [его номинальный размер А_д, допуск на номинальный размер замыкающего звена ГАд, предельные отклонения: верх­нее A- (ES) и нижнее А_н (Ei)] и по нему рассчитывает со-

Ад Ад

ставляющие звенья A_t (номинальный размер, допуск и отклоне­ния). Задача решается тремя способами: 1) попыток; 2) равного допуска и 3) единого квалитета [3, 10].

Обратная задача заключается в том, что когда известны номи­нальные размеры всех составляющих звеньев размерной цепи A_t, Б{ и т. д., их допуски TA_t, предельные отклонения А_Вд^ и Д_Нд^ находят замыкающее звено (его номинальный размер, допуск и предельные отклонения).

Решают эту задачу в приведенной ниже последовательности. 1. Номинальный размер замыкающего звена А_д определяют по формуле

где т — общее число звеньев (например, на рис. 10.5, а т = 3; на рис. 10.5, в т — 6); A_t — составляющие звенья; \_г — переда­точное отношение (для плоских размерных цепей £_г — ±1).

Учитывая направленность звеньев [для увеличивающих звеньев (-{-) и для уменьшающих минус (—)!, формулу (10.1) можно преобразовать:

3. Предельные отклонения размера замыкающего звена опре­деляют по формулам:

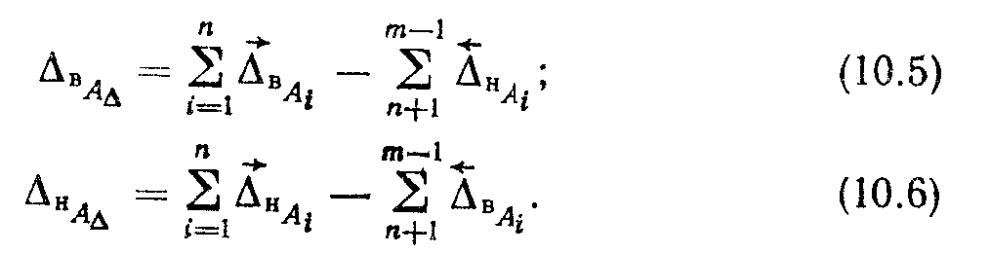Используя формулы (10.2)—(10.6), можно рассчитать как за­мыкающие звенья, так и одно из составляющих при известных остальных и замыкающего звеньев.

Пример. На рис. 10.5, б замыкающим звеном (£д) является зазор между установленной шестерней и торцом втулки. На рис. 10.5, д представлена схема размерной цепи Б. Увеличивающим звеном в этой сборочной единице является звено 5_Ь уменьшающими — звенья £₂ и £₃. Примем £, = 100±g;g|; £₂ = = 40_₀.₁₆ и Б₃ = 60iJ5;JJ5 (точность звеньев ориентировочно равна квалитету точности 11-му). Звено Б₂ является компенсирующим; при решении задачи при­нимаем его за уменьшающее звено.

Решая обратную задачу, находим номинальный размер замыкающего звена (£д) по формуле (10.1):

Допуск на замыкающее звено находим по формуле (10.3):

Верхнее предельное отклонение замыкающего звена определяем по фор­муле

Аналогичные задачи можно решать методом расчета размер­ных цепей с применением теории вероятности, т. е. методом не­полной взаимозаменяемости.