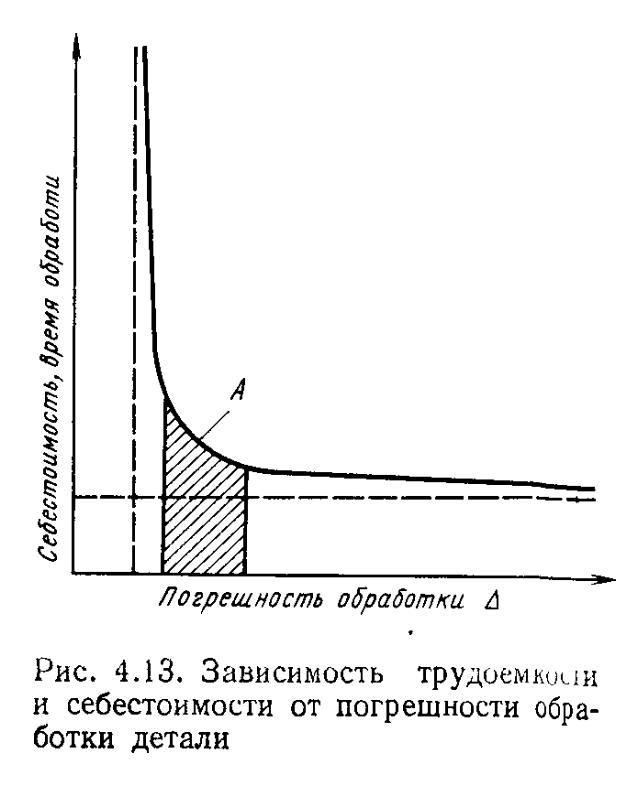
4.3. Экономическая точность обработки

Экспериментальными исследованиями установлено, что ^тРУДоемкость и себестоимость изготовления деталей связаны точностью определенными зависимостями (рис. 4.13). Точность,соответствующая участку А, является экономической точ­ностью обработки. Обычно ког­да говорят о точности какого-либо метода обработки, то имеют в виду значение точно­сти, соответствующее некото­рой точке на участке А.

Экономической точностью какого-либо метода обработки на данном участке развития техники называют точность, обеспечиваемую в нормальных условиях работы, при исполь­зовании исправного оборудо­вания, инструментов стандарт­ного качества, персонала сред­ней квалификации и при затра­те времени и средств , не превы­шающих затрат для Других, сопоставимых с рассматриваемым методом. Таблицы экономической точности обработки приво­дятся в различных справочниках по вопросам технологии ма­шиностроения, например в [21 ].

4.4. Статистические методы исследования точности обработки и определения суммарной погрешности

Погрешностью обработки можно подразделить на систе­матические и случайные.

Систематической погрешностью называют погрешность, кото­рая для всех деталей рассматриваемой партии остается постоянной или же закономерно изменяется при переходе от каждой детали к следующей.

Случайной погрешностью называют погрешность, которая для различных деталей рассматриваемой партии имеет различные значения, причем колебание этих значений в партии не подчиня­ется какой-либо закономерности. Случайные погрешности вызы­ваются действием факторов случайного характера. Например, колебание деформации системы станок—приспособление—инстру­мент—заготовка происходит в результате изменения нормальной составляющей силы резания Р_у, которое неизбежно возникает в результате колебаний в пределах установленного допуска раз­меров и твердости заготовки. К случайным следует отнести также погрешности установки и ряд других.

Случайные погрешности, суммируясь с систематическими, приводят к рассеянию суммарной погрешности, а следовательно, — к рассеянию действительных размеров. Систематические"погреш ности можно заранее предвидеть и учесть соответствующими расчетами/

Случайные погрешности относят к категории случайных вели­чин. Случайные величины и законы их распределения (рассеяния) изучаются в теории вероятностей и математической статистике, использование которых для исследования точности обработки поз­воляет учитывать случайные погрешности.

Вероятностью х какого-либо события называют отношение числа т случаев, благоприятствующих этому событию, к общему числу п всех равновозможных, несовместимых и независимых друг от друга случаев: Р_х = т/п.

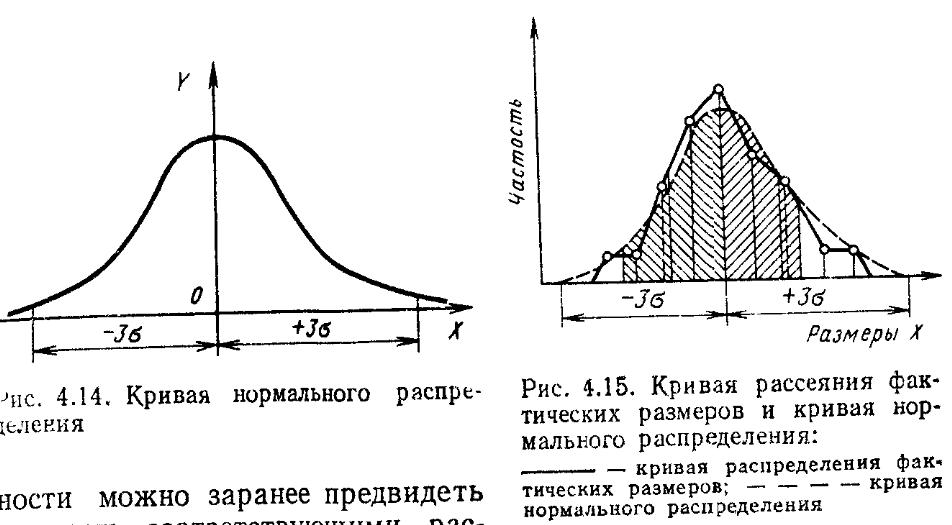
Из всех законов распределения случайных величин наиболь­шее практическое значение имеет так называемый закон нормаль­ного распределения, изображаемый кривой распределения Гаусса. Уравнение этой кривой имеет следующий вид (рис. 4.14): у где о — среднеквадратическое отклонение.

Практически вся (99,73%) площадь кривой нормального рас­пределения находится в пределах ±3а.

Среднеквадратическое отклонение для дискретных (прерывиотых) случайных величин

Кроме закона нормального распределения, в математической статистике используют и законы распределения существенно по­ложительных величин, равной вероятности, закон Симпсона (распределение по треугольнику) и другие.

Практическое использовние закона нормального распределения можно пояснить конкретным примером. После обработки партии заготовок (например, 100 шт.) на предварительно настроенном станке (по методу автомагического получения размеров) их раз­меры измеряют. Результаты измерений заносят в таблицу, в которой также отражаются следующие данные: интервалы значений действительных размеров (случайные значения х); число деталей с действительными размерами данного интервала K_t (частота); ^тх — Ki/n — относительная частота, или частость.

Сумма всех частот должна быть равна числу деталей в исследуем ой партии: , а сумма всех частостей — единице

Полученное эмпирическое распределение можно пред­ставить графически (рис. 4.15). Полученная таким образом кривая получила название практической кривой распределения.

В теории вероятностей доказывается, что между частостью и вероятностью существует приближенное равенство, точность которого возрастает о увеличением числа наблюдений:

Близость практической кривой распределения к кривой нор­мального распределения оценивается либо визуально, либо с по­мощью критериев, которые рекомендуются в курсе математиче­ской статистики. Для изучения распределения случайных вели­чин в практических условиях используют две основные статисти­ческие характеристики:

1) X — среднеарифметическое значение случайной величины

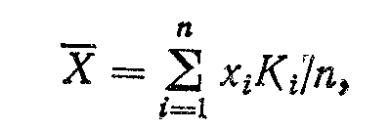(4.8)

где х, — середина интервала наблюдаемых значений х, разбитых на интервалы; Ki — частота значений х; п — общее число на­блюдений;

2) о — среднеквадратическое отклонение случайной величины от ее среднего значения:

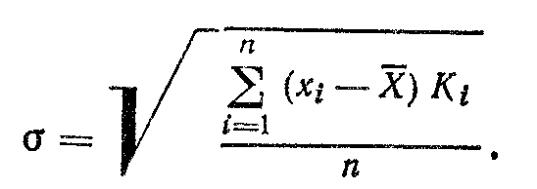(4.9)

По результатам многочисленных экспериментальных исследо­ваний машиностроителями сделан очень важный практический вы­вод: если при изготовлении партии деталей на настроенном станке систематические погрешности были постоянными, то распределение действительных размеров в такой партии подчиняется закону нормального распределения.

В настоящее время для статистических исследований точности обработки и определения суммарной погрешности обработки ис­пользуются два метода: метод кривых распределения и больших выборок; метод точечных диаграмм и малых выборок.

Выборкой называют часть деталей, отобранных из изучаемой партии определенным способом. Если в выборке имеется более

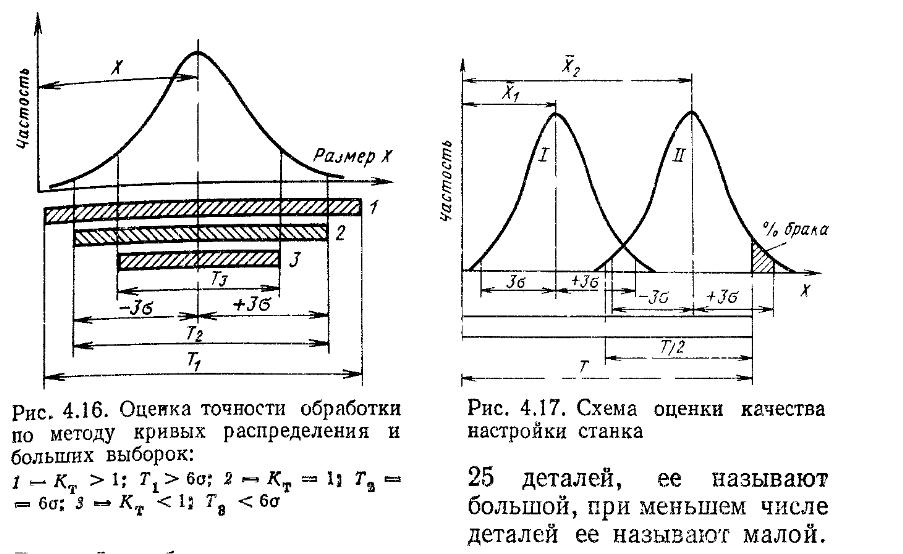
Рис. 4.17. Схема оценки качества настройки станка

25 деталей, ее называют большой, при меньшем числе деталей ее называют малой. Теорией выборочного метода доказывается, что если совокуп­ность значений случайной величины х подчиняется какому-либо закону распределения, то и большая выборка из этой совокуп­ности будет также подчинена этому же закону. При этом статисти­ческие характеристики распределения выборки (среднеарифмети­ческое значение X и среднеквадратическое отклонение s) будут близки по своим значениям к соответствующим характеристикам (Х₀ и а) совокупности, из которых взята эта выборка. Для стати­стических исследований точности обработки методом кривых рас­пределений обычно принимают объем выборки m ^> 50. При ш = 50 погрешность определения Х₀ по значению X составляет ±0,14s, а при определении о по s погрешность составляет ±0,ls. Отмеченные приближения вполне допустимы для практических целей. Метод кривых распределения заключается в следующем. При изготовлении деталей на настроенном станке берут текущую вы­борку (последовательно отбирают детали со станка по мере их изготовления) объемом m > 50. По определенной методике производят измерения деталей данной выборки. Результаты из­мерений заносят в специальную таблицу и строят практическую кривую распределения. Убедившись в близости этой кривой к кри­вой нормального распределения по соответствующей оценке, можно определить суммарную погрешность, а следовательно, Достигнутую точность обработки. Определяются значения а, X по формулам (4.8) и (4.9). Суммарная погрешность обработки ^д = бог. Сравнивая погрешность А с допуском Т на размер оце­нивают точность обработки (рис. 4.16). Коэффициент точности = 776а).

При условии правильной настройки станка изготовление деталей может осуществляться без брака, если К_т > 1,0. При /С_т •< 1,0 весьма вероятно появление бракованных деталей, число которых может быть определено соответствующими расчетами. Обработка считается надежной при Д'_т > 1,2.

Значение X свидетельствует о качестве настройки станка. Может оказаться, что при хорошей точности, но при неудовлетво­рительной настройке станка (Х₂) размеры некоторой части деталей выйдут за пределы поля допуска (рис. 4.17), и они будут забра­кованы.

Метод кривых распределения и больших выборок позволяет получить объективную оценку точности выполнения данной опера­ции на конкретном оборудовании. Однако при его использовании не учитывается последовательность обработки заготовки.

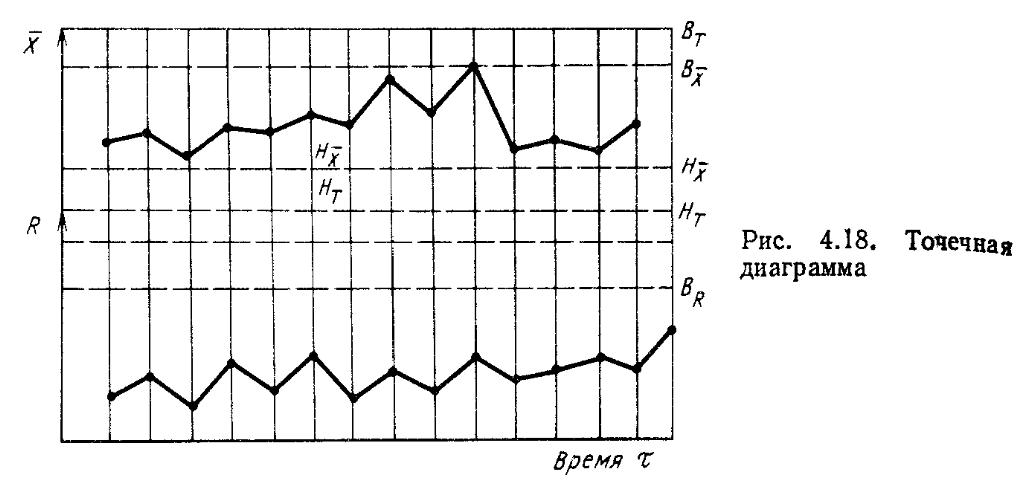
Метод точечных диаграмм и малых выборок заключается в следующем. В процессе обработки детали берут со станка малые текущие выборки (обычно по 5 шт.) в течение рабочей смены через определенные промежутки времени (например, через 15—-30 мин). Детали измеряют универсальным измерительным инструментом. Определяют среднеарифметическое значение выборки X. Вычисля­ют также размах выборки R — разность между наибольшим х_тх и наименьшим x_min размерами выборки: R = дг_шах — х_т1п. Размах характеризует р_ассеяние размеров в малой выборке. Между сред­ним значением R размаха ряда выборок и среднеквадратическим отклонением а для всей партии, из которой берутся выборки, существует определенная связь. (В курсах математической ста­тистики приведена формула, выражающая эту связь).

Для построения точечной диаграммы вычерчивают графики, в которых по оси ординат наносят значения X я R, а по оси абс­цисс—время взятия выборок или их номера (рис. 4.18). На диаграммы наносят контрольные линии В_Т; Я_т; Вх; Hj и Яд-Линии В_г и Я_т называют линиями верхнего и нижнего тех­нических пределов; они соответствуют наибольшему и наимень-50 нему предельным размерам, заданным чертежом; Вх, Их и B_R — онтрольные значения амплитуды колебаний выборочных средних и размахов; их определяют по формулам, которые приведены в кур­сах математической статистики.

Верхняя Вх и нижняя Hj контрольные линии устанавли­вают границы возможных колебаний выборочных средних X при нормальном ходе процесса. Выход точки за границы этих линий является сигналом, по которому следует произвести под-наладку станка. Выход точки R за линию В_в сигнализирует о недопустимом рассеянии размеров, вызванном неисправностями станка, которые необходимо устранить.

Рассмотренный метод позволяет следить за ходом процесса и изменением точности станка во времени. Выход точки за конт­рольные линии является предупреждением о том, что возможно появление брака. Следовательно, необходимо соответствующее вмешательство в обработку заготовки.

Статистические методы контроля не отражают степень влияния отдельных факторов на образование суммарной погрешности и, следовательно, не дают необходимой информации для управления точностью процесса обработки заготовок. Это является главным недостатком статистических методов, который в значительной мере устраняется при использовании расчетно-аналитического метода определения суммарной погрешности.