Структкрный метод
Структурной схемой называется графическая модель системы, в которой каждому элементу ставится в соответствие его динамическая характеристика. Такая схема наглядно отражает состав системы и связи между отдельными ее составляющими.
Структурная схема может быть построена на основе, как дифференциальных уравнений, так и передаточных функций.
Любая сложная структурная схема может быть изображена с помощью основных типов соединений:
- параллельное соединение;
- последовательное соединение;
- соединение с обратной связью.
2.8.1 Структурные схемы.
1. Параллельное соединение звеньев.
При параллельном соединении входные сигналы всех звеньев одинаковы и равны входу системы (рис. 2.32).
Рис. 2.32. Структурная схема системы с параллельным соединением звеньев.
Общий выход системы равен сумме выходных сигналов отдельных звеньев.
Уравнение выходных сигналов каждого звена:
- эквивалентная передаточная функция
всей системы.
Таким образом, передаточная функция системы параллельно соединительных звеньев равна сумме передаточных функции отдельных звеньев, и в структурной схеме их можно заменить одним эквивалентным звеном с передаточной функцией Wэ(p).
2. Последовательное соединение звеньев.
При последовательном соединении выход предыдущего звена подается на вход последующего (рис. 2.33):
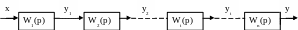
Рис. 2.33. Структурная схема системы с последовательным соединением звеньев.
В этом случае имеем систему уравнений:
….
С учетом того, что выходной сигнал последнего звена является выходом всей системы, получим:
Передаточная функция последовательно соединенных звеньев равна произведению передаточных функций всех звеньев. Это значит, что их можно заменить одним эквивалентным звеном с передаточной функцией Wэ(p).
3. Соединение с обратной связью.
Обратной связью называют передачу сигнала с выхода звена на его вход (рис. 4.4):
Рис. 2.34. Структурная схема соединения с обратной связью.
Обратная связь может быть положительной:
;
и отрицательной
В линии обратной связи в общем случае
может быть включено звено, в котором
выходной сигналy
преобразуется в соответствии с
передаточной функцией
в сигнал
Иногда это звено может отсутствовать,
тогда
.
Найдем соотношение между передаточной функцией замкнутой системы Wз(р)и передаточными функциями отдельных звеньев Wп(р) и Wос(р).
;
;
.
Исключив из полученной системы уравнений (р) и уос(р), найдем общее уравнение системы:
.
Откуда получаем передаточную функцию замкнутой системы:
.
Отметим, что формула выведена для положительной обратной связи. Аналогичный вывод для отрицательной обратной связи дает:
.