Лекция №5

2.7. Динамические звенья и их характеристики

Типовые динамические звенья САУ подразделяются на обыкновенные и особые.

1. Обыкновенные типовые динамические звенья описываются дифференциальными уравнениями 1-го или 2-го порядка или передаточной функцией 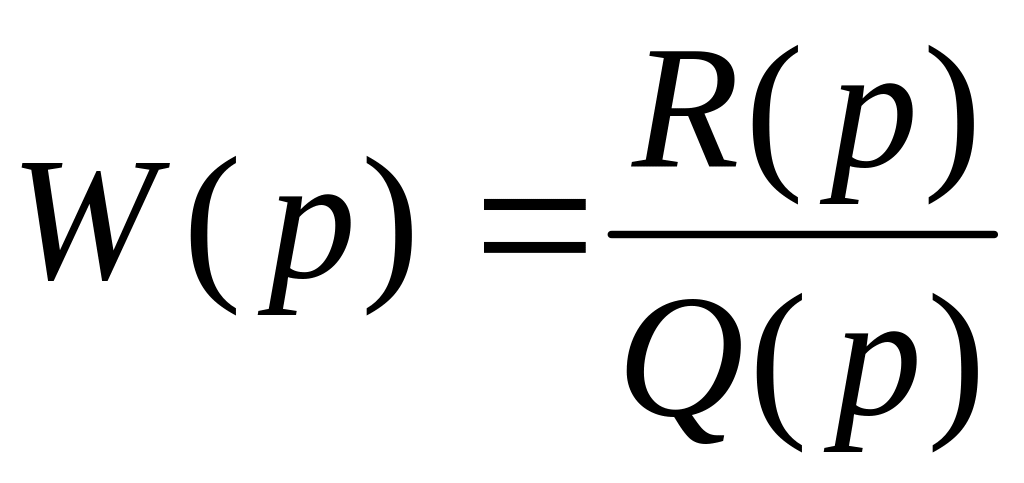, являющейся математической моделью элемента САУ.

2. Особые динамические звенья – неустойчивые звенья, звенья с распределенными параметрами, дискретные звенья. Они составляют основу особых САУ: САУ с переменными параметрами, САУ с запаздыванием и распределенными параметрами, импульсные, дискретные, нелинейные и т.д.

Обыкновенные ТДЗ подразделяют на 3 основные группы:

1. Звенья статического или позиционного типа, где 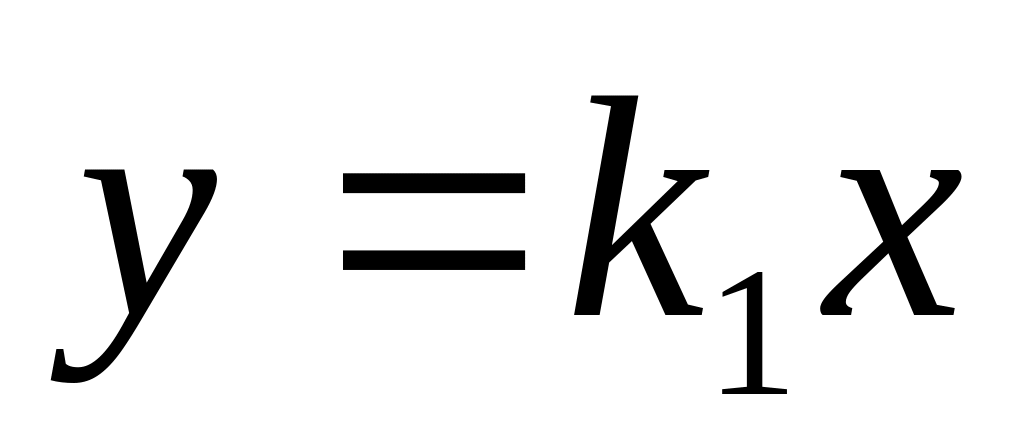, 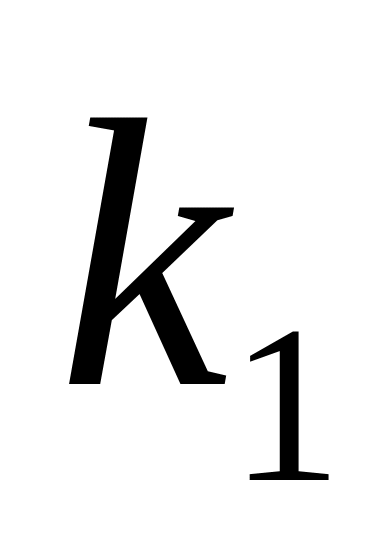- коэффициент передачи звена.

2. Звенья интегрирующего типа, где

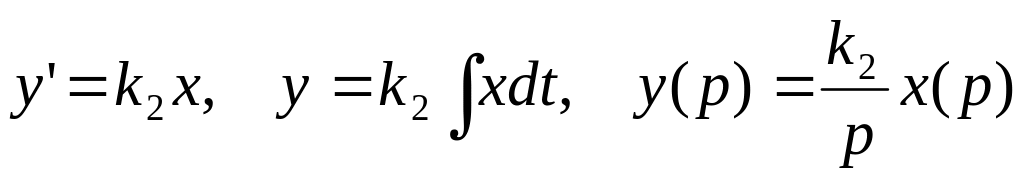
3. Звенья дифференцирующего типа, где 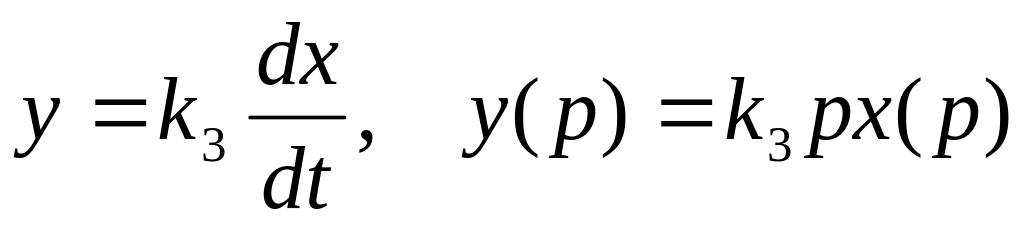. Дифференцирующие звенья еще называют форсирующими.

Рассмотрим уравнения, переходные и частотные характеристики часто встречающихся типовых звеньев.

2.7.1 Статические звенья.

Все статические звенья в установившемся режиме описываются одинаковым уравнением .

1. Статическое идеальное звено (пропорциональное).

Его уравнение и в статике и в динамике y(t)=kx(t), где k – коэффициент усиления звена. Т.о. выходной сигнал усилительного звена в любой момент времени равен входному сигналу, умноженному на коэффициент усиления. Передаточная функция усилительного звена следует из его уравнения, после преобразования его по Лапласу: y(p)=kx(p), откуда .

После замены р на iω получим АФХ:

W(iω)=k, откуда АЧХ: А(ω)=k; ФЧХ: φ(ω)=0.

Т.о. АФХ идеального статического звена представляет собой точку на действительной положительной полуоси, расположенную от начала координат на расстоянии k.

В ответ на единичное ступенчатое воздействие сигнал на выходе мгновенно достигает величины в k раз большей, чем на входе и сохраняет это значение. При k=1 звено никак себя не проявляет, а при k=-1 инвертирует входной сигнал.

Любое реальное звено обладает инерционностью, но с определенной точностью некоторые реальные звенья могут рассматриваться как безынерционные, например, жесткий механический рычаг, редуктор, потенциометр, электронный усилитель и т.д.

2. Статическое звено первого порядка (апериодическое).

Линейное дифференциальное уравнение апериодического звена:

,

где Т – постоянная времени звена; k – коэффициент усиления.

Примером такого звена может служить любая цепочка, включающая сопротивление и емкость независимо от их физической природы.

Передаточная функция получается из уравнения звена:

Частотные характеристики описываются формулами:

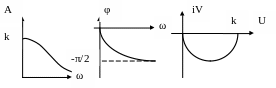
Рис. 2.12. Частотные характеристики апериодического звена первого порядка.

Уравнение кривой разгона получается как решение дифференциального уравнения апериодического звена при нулевых начальных условиях и x(t)=1(t) или из уравнения передаточной функции апериодического звена при x(p)=1/p. Тогда

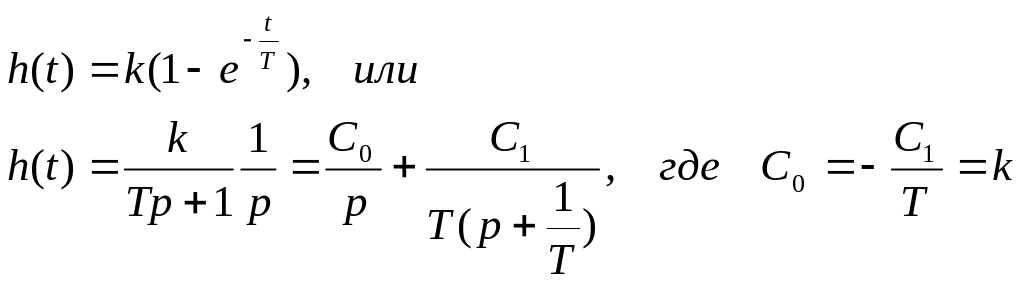
Весовая функция находится как производная от кривой разгона

Соответствующие характеристики представлены на рис. 2.13.

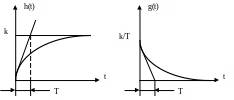
Рис. 2.13. Переходные характеристики апериодического звена первого порядка.

Если эти характеристики получены экспериментально, по ним можно определить значения T и k, как показано на рисунках, и, т.о. получить уравнение звена.

Величина постоянной времени Т определяет инерционность звена: чем она больше, тем длительнее переходный процесс в звене. На практике за длительность переходного процесса принимают время, которое прошло от начала процесса до момента, когда выходная величина достигла 95% от ее конечного установившегося значения

Логарифмическая характеристика (л.а.х.):

(*)

При малом значении частоты . Соответственно характеристика будет представлять собой прямую, параллельную оси абсцисс, и проходящую на уровне . Это есть первая асимптота, к которой стремится л.а.х. при . С другой стороны на больших частотах при , т.е. .

В этом случае характеристика представляет собой прямую, имеющую наклон -20 дБ/дек. Действительно, при увеличении частоты в 10 раз, т.е. на декаду

.

Т.о. величина L() уменьшилась на 20lg10, т.е. на 20 дБ.

Эта линия является второй асимптотой, к которой стремится к график л.а.х. при . Обе асимптоты пересекаются на частоте: ,

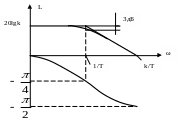
Рис. 2.14. Логарифмическая частотная характеристика апериодического звена.

Частота называется сопрягающей частотой.

Таким образом, расхождение между истинной и ассимтотической л.а.х. составляет 3дБ, поэтому при практических построениях л.а.х. апериодических звеньев используют обычно ассимтотические л.а.х..

Примером апериодических звеньев первого порядка являются:

1. генератор постоянного тока;

2. двигатель любого типа (электрический, пневматический и т.д.), механические характеристики которого – прямые линии, для различных входных сигналов;

3. резервуар с газом, жидкостью…;

4. нагревательная печь;

5. термопара;

6. электромагнитные, гидро-, пневмоусилители и т.д.

3. Статическое колебательное звено II-го порядка.

,

где - постоянные времени, k – коэффициент усиления.

Характеристическое уравнение запишется в виде:

.

Корни этого уравнения 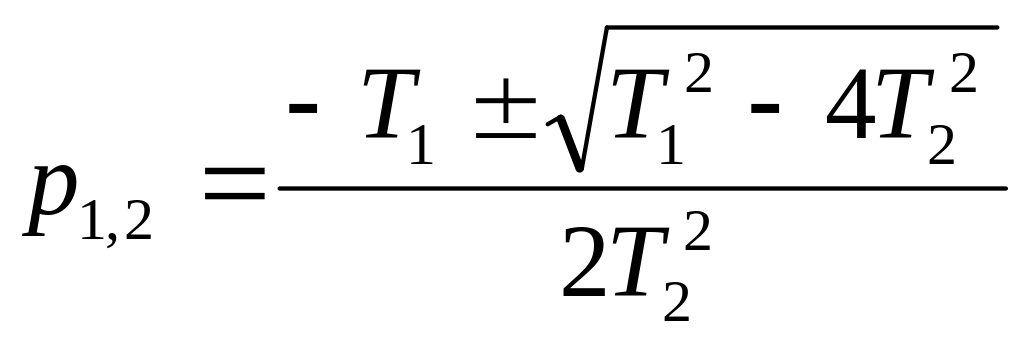будут комплексными при условии . Если это неравенство не выполняется, корни этого уравнения будут действительными, что соответствует случаю апериодического звена II-го порядка, для которого .

Уравнение установившегося статического режима этого звена имеет тот же вид, что и для усилительного и апериодического звеньев:

Передаточная функция:

Частотные характеристики (рис. 2.15.)

АФХ: ; АЧХ: ;

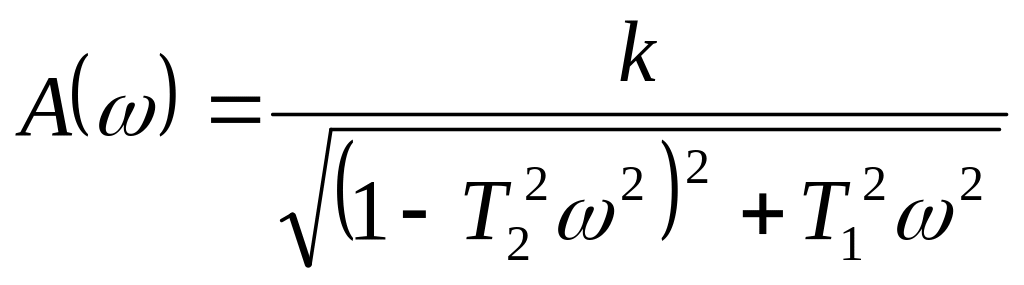ФЧХ: .

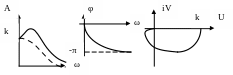
Рис. 2.15. Частотные характеристики колебательного звена.

Как видно из формулы для АЧХ при малых значениях , когда , наблюдается некоторое увеличение А() по сравнению с апериодическим звеном (показана пунктиром), причем при малых значениях отношения T₁/T₂ на графике А() появляется максимум, в предельном случае при , на частоте 1/T₂ получается резонансный пик (консервативное звено).

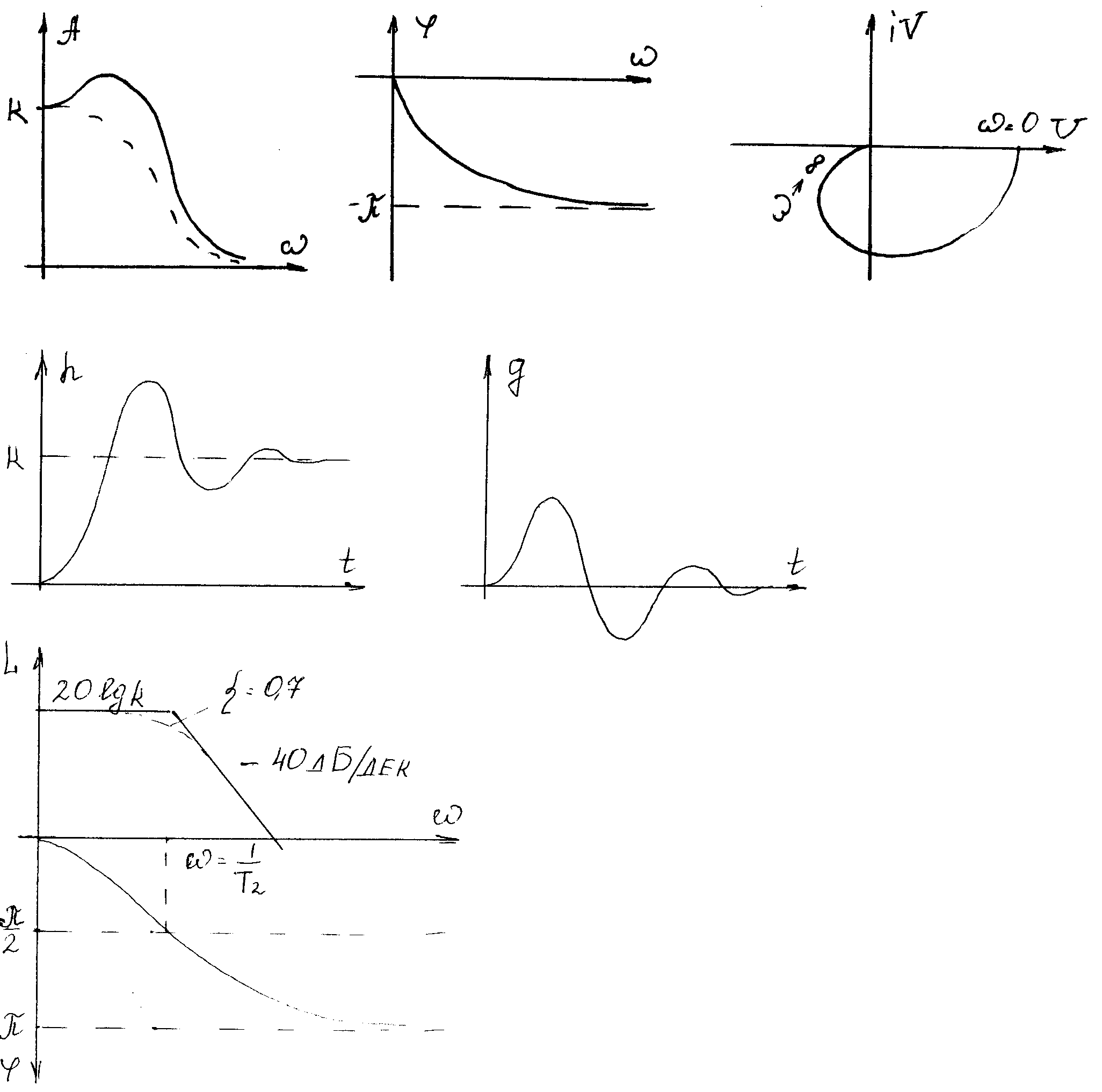
Рис. 2.16. Переходные функции колебательного звена: а) – кривая разгона; б) – импульсная переходная функция.

Уравнение кривой разгона в операторной форме имеет вид:

По таблицам оригиналов находим:

По экспериментально снятой кривой разгона (переходной функции) можно найти параметры .

Асимптотическая л.а.х. представляет собой ломаную линию, состоящую из двух асимптот, к которым стремится л.а.х. при и при . Одна асимптота – линия, параллельная оси абсцисс и отстоящая от нее на расстояние , Другая асимптота имеет наклон -40 дБ/дек. Точка пересечения соответствует частоте 1/T₂.

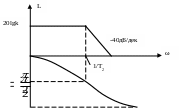
Рис. 2.17. Логарифмическая характеристика колебательного звена.

Уравнение первой асимптоты получается из уравнения для л.а.х.:

.

При , .

Уравнение второй асимптоты соответствует . При этом

.

Из последнего выражения следует, что при увеличении частоты на декаду L() снижается на 40 дБ, что и определяет указанный выше наклон – 40дБ/дек.

Введем условное обозначение

При расхождение между асимптотической и истинной л.а.х. не превышает 3дБ, как и в случае апериодического звена. Поэтому для звеньев с таким значением  можно пользоваться асимптотической л.а.х. Фазовая частотная характеристика представлена ниже, вместе с л.а.х

Примеры колебательного звена: электрический резонансный контур RLC; электрический двигатель при достаточно большой постоянной времени якоря; упругие механические передачи.

4. Статическое звено второго порядка (апериодическое II-го порядка).

Такое звено описывается аналогичным уравнением, как и колебательное, только здесь . Обобщенное уравнение второго порядка имеет вид:

.

Апериодическое звено II-го порядка можно представить как цепочку последовательно соединенных двух звеньев I порядка, с постоянными времени и и коэффициентами усиления k и 1.

Общая передаточная функция цепочки будет равна:

Следовательно, уравнение звена в операторской форме запишется в виде:

,

откуда получается дифференциальное уравнение:

.

Частотные характеристики апериодического звена II-го порядка (рис. 2.18):

АФХ:

АЧХ:

ФЧХ:

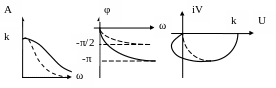
Рис. 2.18. Частотные характеристики апериодического звена II-го порядка

На рис. 2.18 пунктиром показаны частотные характеристики звена I-го порядка с коэффициентом усиления k и постоянной времени Т₁. Как видно из рисунка, добавление другого звена I-го порядка уменьшает значение модуля АФХ и увеличивает отставание по фазе для каждой частоты по сравнению с одноемкостным звеном.

Уравнение кривой разгона (переходной функции) в операторной форме запишется в виде:

.

Оригинал этой функции имеет вид:

где ; ; .

График представляет собой неколебательную кривую, имеющую точку перегиба и асимптотически стремящуюся к k (рис. 2.19).

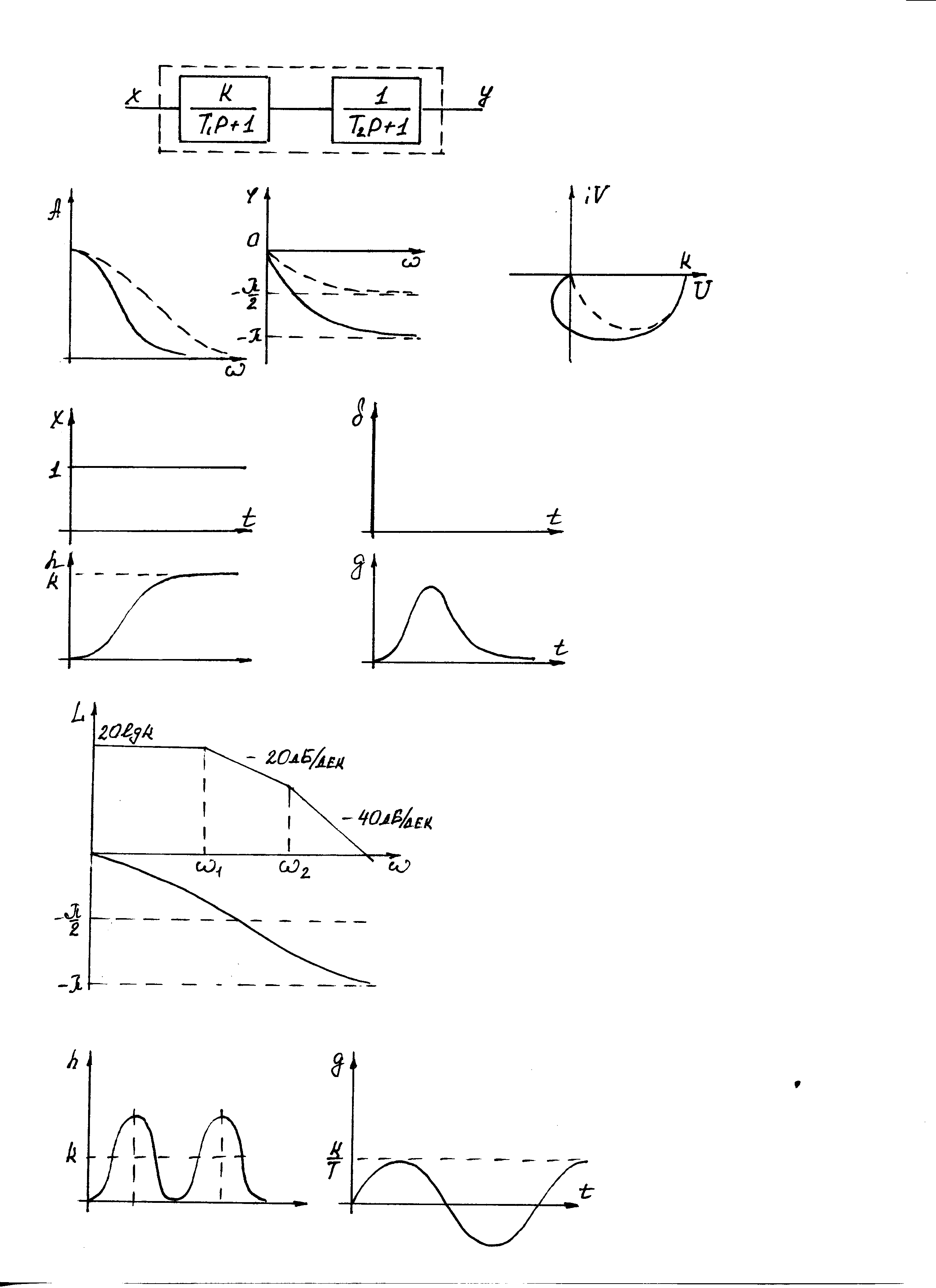
а) б)

Рис. 2.19. Переходные характеристики апериодического звена II-го порядка: а) - кривые разгона; б) – импульсная переходная функция.

Уравнение импульсной переходной функции получим из формулы для h(t) путем дифференцирования:

Логарифмическая характеристика (рис. 2.20):

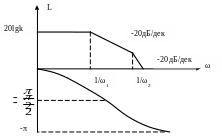
Рис. 2.20. Логарифмическая характеристика апериодического звена II-го порядка.

(₁ = 1/T₁; ₂ = 1/T₂).