Линейный сток

Свободный линейный сток – это пространственный воздушный поток, устремленный к бесконечно длинной прямой линии, в которой поток поглощается. Воздух со всех сторон устремляется к линии поглощения потока, а точки с одинаковым значением скорости образуют цилиндрические поверхности.

Скорость движения воздуха в любой точке свободного линейного стока связана с расстоянием до поглощающей поток линии уравнением неразрывности:

(2.5)

L/l - удельный секундный расход воздуха; r – расстояние от произвольной точки до линии поглощения потока.

Если с линией стока совместить оcь y, то составляющие скорости свободного линейного стока будут равны:

(2.6)

где x, z – координаты точки, в которой нужно найти значение скорости воздуха; .

Для линейного стока воздуха, ограниченного с одной стороны плоской стенкой, скорость течения воздуха по сравнению со свободным стоком удваивается:

(2.7)

Если линия поглощения расположена в ребре двугранного угла, грани которого составляют плоский угол , то скорость течения воздуха на заданном расстоянии определяется формулой

(2.8)

Рассмотрим взаимодействие двух ограниченных с одной стороны линейных стоков одинакового удельного расхода, расположенных в плоскости x=0 параллельно оси y на расстоянии 2b один от другого.

Начало координат поместим в точку, разделяющую расстояние между полюсами стоков пополам.

Тогда, для произвольной точки полупространства, составляющие скорости, образованного независимым действием одного линейного стока равны:

(2.9)

Составляющие скорости потока, образованного независимым действием другого стока составляют:

(2.10)

Результирующие составляющие скорости потока, образованного взаимодействием двух одинаковых линейных свободных стоков, является суммой найденных составляющих:

(2.11)

В плоскости симметрии . Нулевая скорость свидетельствует об отсутствии потока; воздуха не проводится сквозь плоскость, и она может быть заменена непроницаемой поверхностью.

Таким образом, формулы отражают результат взаимодействия двух одинаковых свободных линейных стоков или результат взаимодействия одного линейного стока с непроницаемой поверхностью.

Сток воздуха к прямоугольным отверстиям

Рассмотрим прежде всего сток воздуха к бесконечно длинному отверстию конечной ширины, устроенному в плоской стене. Поместим начало координат в центр отверстия так, чтобы ось x была направлена навстречу потоку воздуха. Ширина 2B, а секундный удельный расход воздуха L/l. Сток воздуха к отверстию представим как результат взаимодействия бесконечно большого числа бесконечно малых линейных стоков воздуха. Разделим мысленно всасывающее отверстие на бесконечно тонкие полоски шириной db.

Удельный расход воздуха, поглощаемый каждой из таких полосок, будет элементарным и при условии равномерного всасывания определится следующим соотношением

Выделим одну из элементарных полосок на расстоянии b от начала координат и допустим, что воздух из полупространства стекает только к ней одной. Образованный таким образом элементарный сток подчиняется закономерностям линейного стока.

Составляющие скорости воздуха, образуемой таким элементарным стоком:

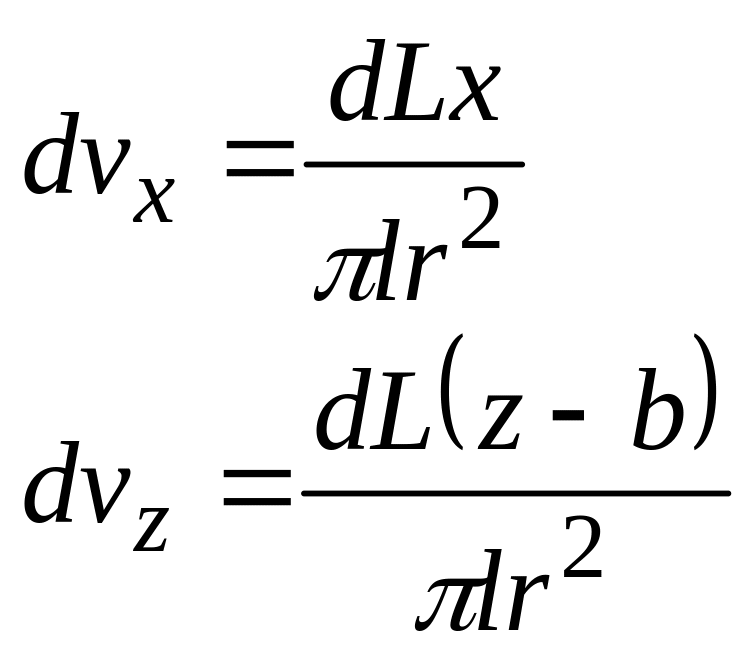(2.12)

Подставим в эти соотношения значения dL и r :

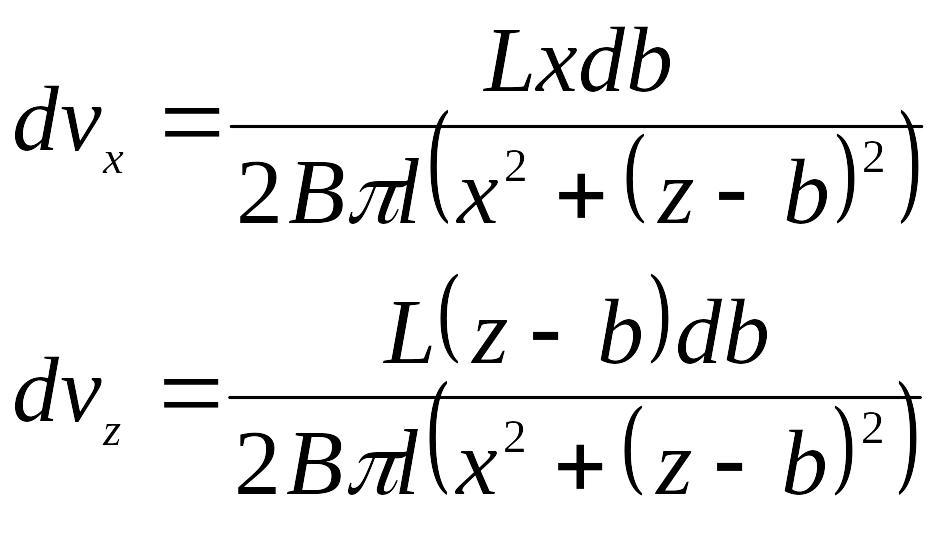_(2.13)

Интегрируя эти уравнения в пределах от –B до B дает значения составляющих скорости стока ко всасывающему отверстию:

(2.14)

Рассмотрим случай взаимодействия двух одинаковых полуограниченных стоков воздуха ко всасывающим отверстиям конечной ширины, расположенным в плоскости x = 0 параллельно оси y и симметрично относительно нее.

Обозначим расстояние от плоскости симметрии (z = 0) до ближайших кромок щелевидных отверстий через B₀, а удаленных – через B₁. Теперь достаточно проинтегрировать уравнения в этих пределах, чтобы получить значения составляющих скорости к двум параллельным отверстиям конечной ширины:

(2.15)