2.4. Воздушные фонтаны

Воздушным фонтаном называется струя нагретого или охлажденного воздуха, испытывающая заметное влияние гравитационных сил.

В случае горизонтального или наклонного истечения воздушного фонтана гравитационые (архимедовы) силы постепенно отклоняют нагретую струю вверх, а охлажденную - вниз от направления истечения и придают ей характерную изогнутую форму. В случае вертикальной подачи нагретого или охлажденного воздуха гравитационные силы увеличивают или уменьшают торможение струи, образующей фонтан.

Восходящий воздушный фонтан охлажденного воздуха или ниспадающий воздушный фонтан нагретого воздуха за счет гравитационных сил полностью затормаживается и, начиная с некоторого уровня, разворачивается назад к своему истоку.

Приточная струя, температура которой сколь угодно отличается от температуры окружающего ее воздуха, на близких к истоку расстояниях распространяется прямолинейно как изотермическая; гравитационные силы еще не успели оказать на нее заметное действие.

Приточная струя, температура которой хоть немного отличается от температуры окружающего ее воздуха, начиная с некоторого расстояния распространяется как воздушный фонтан.

В конце своего существования воздушный фонтан стремится превратиться в вертикальный конвективный поток.

Теория воздушного фонтана обобщает его свойства и как приточной струи, и как конвективного потока, а также позволяет установить те граничные расстояния, на которых один вид течения сменяется другим.

Компактные воздушные фонтаны, истекающие под углом к горизонту

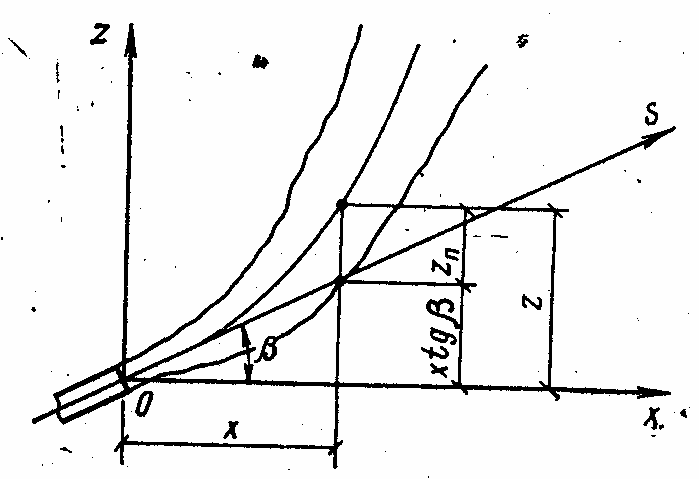
Рис. 2.6. Воздушный фонтан, истекающий под углом к горизонту

Если плотность приточного воздуха не отличается от плотности воздуха помещения, струя распространяется прямолинейно вдоль луча Os, причем уравнение ее оси выражается в виде . При истечении нагретого воздуха струя изгибается вверх и отклоняется от луча на отрезка z_п . В этом случае уравнение изогнутой оси воздушного фонтана должно быть представлено двучленом

(2.93)

Для оценки величины z_п выделим в области центрального потока элементарный объем воздуха dV и проследим за его перемещениями.

Масса выделенного объема воздуха

(2.94)

Подъемная (архимедова) сила, действующая на этот объем,

(2.95)

Вертикальное ускорение, вызванное действием силы,

(2.96)

Замена отношения плотности соответствующим отношением температур дает:

(2.97)

Ускорение является производной скорости по времени

(2.98)

а элементарное время можно выразить посредством отрезка пути в направлении оси s и скорости частицы в том же направлении

(2.99)

Поэтому для вертикального ускорения можно получить иное выражение:

(2.100)

Сравнивая уравнения (2.97) и (2.98), найдем, что скорость вертикального перемещения выделенного объема воздуха определяется интегралом

(2.101)

Скорость движения и температура воздуха на оси приточных струй одинаково зависят от расстояния, и эта зависимость обобщается равенством

(2.102)

Но скорость является производной пути по времени:

(2.103)

Исключая время по условию (2.99), получим другое выражение для скорости вертикального перемещения:

(2.104)

Сравнение уравнений (5) и (6) приводит к интегралу, определяющему искомое вертикальное перемещение выделенного объема воздуха:

Для воздушного фонтана, образованного компактной струей, связь между скоростью и расстоянием выражается зависимостью

(2.105)

Теперь интеграл легко берется:

(2.106)

Замена координаты s на и подстановка значений z_п в исходное уравнение приводят к уравнению изогнутой оси компактного фонтана нагретого воздуха, истекающего под углом к горизонту:

(2.107)

Представим полученное уравнение в другой записи:

(2.108)

где посредством H обозначен комплекс величин, названный геометрической характеристикой компактного воздушного фонтана.

(2.109)

Геометрическая характеристика представляет собой линейный размер, которым однозначно измеряются все характерные размеры воздушного фонтана. В свою очередь она целиком определяется начальными условиями истечения фонтанирующей струи. Характеристику воздушного фонтана можно выразить иначе – посредством секундного количества подаваемого воздуха и площади приточного отверстия:

(2.110)

или скорости истечения

(2.111)

Для того, чтобы оперировать с положительными значениями начальной разности температур и угла наклона (если они отрицательны), в уравнении (2.108) поставлены два знака, причем знак плюс соответствует истечению нагретой струи вверх или охлажденной струи вниз, а знак минус – истечению нагретой струи вниз или охлажденной струи вверх.

В случае горизонтального истечения уравнение оси воздушного фонтана упрощается:

(2.112)

Выявим расстояние, на котором ось горизонтального воздушного фонтана не слишком сильно отходит от направления истечения.

Тангенс угла наклона между касательной к оси воздушного фонтана и горизонтальной осью x есть производная dz/dx. Отсюда расстояние, на котором касательная к изогнутой оси воздушного фонтана будет составлять с осью x заданный угол ,

(2.113)

До какого расстояния воздушный фонтан можно рассматривать как приточную струю, т.е. где касательная к оси воздушного фонтана наклонена к оси x не более чем, например, на 15 градусов?

Ответ следует из формулы

Округленно

(2.114)

Поставим следующий вопрос: начиная с какого расстояния воздушный фонтан можно рассматривать как конвективный поток, т.е. где касательная к оси воздушного фонтана наклонена к оси x не менее чем, например, на 75 ?

Ответ следует из той же формулы

. (2.115)

Таким образом, на расстоянии, меньших 0.5H, направление воздушного фонтана мало отличается от направления, истечения приточной струи, а на расстояниях, превышающих 2H , мало отличается от вертикального направления конвективного потока.

Рассмотрим форму воздушного фонтана охлажденного воздуха, направленного под некоторым углом b выше горизонта. Подобно струе воды воздушный фонтан описывает в вертикальной плоскости дугу.

Расстояние между точками пересечения изогнутой струи фонтана и уровнем приточного отверстия назовем дальнобойностью воздушного фонтана. Она определяется из основного уравнения (2.108) и условия z = 0.

(2.116)

При горизонтальном и вертикальном истечении воздушного фонтана дальнобойность отсутствует.

Имеется, следовательно, некоторый оптимальный угол, истечения воздушного фонтана, обеспечивающий максимальную дальнобойность. Тангенс этого угла найдется из уравнения и составит , т.е. .

Максимальная дальнобойность воздушного фонтана, соответствующая оптимальному углу истечения,

Характер взаимодействия воздушных фонтанов с окружающим воздухом в помещении представлен на рис.2.7.

а

б

Рис. 2.7. Распределение приточного воздуха воздушными фонтанами, направленными

горизонтально ( а – фонтан нагретого воздуха, б – фонтан охлажденного воздуха)