Бақылау сұрақтары:

1. Орташа квадраттық жылдамдық қалай анықталады?

2. Идеал газ күйінің теңдеуін қолданып орташа квадрат жылдамдықты анықтаңыз.

3. Штерн тәжірибесін сипаттап беріңіз.

§9. Барометрлік формула

Ауырлық өрісінде орналасқан газды (ауаны) қарастырайық. Егер молекулалардың жылулық қозғалысы болмаса, онда ауырлық күшінің әсерінен олардың барлығы Жерге құлап, ауа тек Жердің бетінде жұқа қабат түрінде орналасқан болар еді. Егер ауырлық күші болмай, тек молекулалардың жылулық қозғалысы ғана болса, онда молекулалар әлемдік кеңістікке таралып кетер еді. Жердің ауа қабаты, атмосфераның осы күнгі күйінде болуы молекулалардың жылулық қозғалысының және олардың Жерге тартылуының бір мезгілде болуының арқасында. Атмосферадағы молекулалар биіктік бойынша белгілі заңдылықпен таралады және газдың қысымы осындай заңдылықпен биіктік бойынша өзгереді.

Ауаның вертикаль бағанын қарастырайық. Жер бетінде һ₀=0деп алайық, осыған сәйкес қысым P₀ болсын, алһ биіктіктегі қысым Р болсын (9-сурет). Егер биіктік dh-шамаға өзгерсе, онда қысым dP-шамаға өзгереді. Онда

, (9.1)

мұндағы -ауа тығыздығы, -еркін түсу үдеуі. Теріс таңба биіктік артқан сайын қысымның кемитіндігін көрсетеді. Енді тығыздықтың 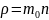екенін ескеріп және молекулалар концентрациясын деп алып, тығыздықты былай өрнектейміз:

.

Енді осы өрнекті (9.1) формулаға қойсақ, мынадай өрнек аламыз:

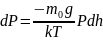(9.2)

Бұл өрнек бірінші дәрежелі дифференциалдық теңдеу болып табылады. Мұндай теңдеуді айнымалыларды бөлу әдісімен шешеміз.

(9.3)

Енді осы өрнектің екі жағын да интегралдасақ, онда мынадай өрнек аламыз:

,

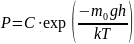(9.4)

Егер h=0(Жер бетінде) болса, онда болады, демек аддитивті тұрақты Жер бетіндегі қысымға тең болады . Олай болса (9.4) теңдеуді мына түрде жазуға болады:

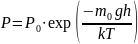(9.5)

Бұл формуладағы молекула массасын әрбір газ үшін есте сақтау қиын, сондықтан оны мольдік масса мен Авогадро саны арқылы өрнектейміз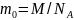 . Енді осы өрнекті (9.5) өрнекке қойып және екенін ескерсек, онда мынадай формула аламыз:

(9.6)

Бұл формуланың көмегімен кез келген биіктіктегі қысымды анықтауға болады, сондықтан оны барометрлік формула деп атайды.

Егер (6) формуладағы hбиіктікті табайық:

(9.7)

Осы формуланың көмегімен және қысымдарын өлшеп биіктікті анықтауға болады. (9.7) формуланың негізінде биіктік өлшегіш аспап жасалады. Оны альтиметр деп атайды.

Бақылау сұрақтары:

1. Ауа молекулаларының Жер бетінде биіктік бойынша таралуы қандай құбылыстармен түсіндіріледі?

2. Жер бетінен биіктік артқан сайын қысым қалай өзгереді?

3. Барометрлік формуланы қорытып шығарыңыз.

§10. Больцман таралуы

формуласындағы экспонента көрсеткішінің алымындағы массасы m₀молекуланың hбиіктіктегі потенциалдық энергиясы екендігі механика курсынан белгілі. Молекула-кинетикалық теорияның негізгі теңдеуінен( ), яғни және пропорционалдықтары орындалады. Сондай-ақ, концентрацияның көлем бірлігіндегі молекулалар саны екенін ескерсек, онда барометрлік формуланы мына түрде жаза аламыз:

(10.1)

Бұл өрнек энергиясы нөлге тең бөлшектердің саны , ал энергиясы бөлшектер саны болатынын көрсетеді. Егер молекулаларға ауырлық күші емес басқа күш өрісінде болса және бөлшектер сол өрісте потенциалдық энергияға ие болса,онда берілген энергияға ие болатын бөлшектер санын былай анықтай аламыз:

.(10.2)

Осы формуланы газ молекулаларының күш өрісінде таралуының формуласы немесе Больцман таралуы деп атайды. Бұл формула жылулық тепе-теңдік жағдайында энергиясы болатын бөлшектердің үлесін анықтауға мүмкіндік береді:

(10.3)

Бақылау сұрақтары:

1. Больцман таралуы нені анықтайды?

2. Больцман таралуына мысалдар келтіріңіз.