§43. Термодинамикалық тепе теңдік шарттары

Термодинамикалық тепе теңдіктегі адиабаталық оқшауланған жүйенің энтропиясы қарастырылатын күйде максимал болсын, демек жылу бермей және алмай өтуі мүмкін шексіз жақын күйлердің энтропияларымен салыстырғанда көп болсын. Бұл жағдайда жүйе жақын күйлерге өз бетімен өте алмайды, демек жүйе орнықты термодинамикалық тепе теңдік күйінде. Шыныда мұндай адиабаттық өту мүмкін болса, онда шарты орындалуы керек. Бірақ бұл шарт энтропияның өсу заңына қайшы, бұл заңға сәйкес адиабаттық өтулерде . Сонымен, термодинамикалық тепе теңдіктің мынадай шарттарын тұжырымдауға болады.

Егер жүйе адиабаттық оқшауланған болса және оның қандай да бір тепе тең күйдегі энтропиясы максимал мәнге ие болса, онда жүйенің бұл күйі термодинамикалық тепе тең күйі болып табылады. Басқаша айтқанда жүйе адиабаталық оқшауланған болса, онда өздігінен ешқандай басқа күйге өте алмайды.

Көптеген жағдайларда термодинамикада жүйені адиабаталық қоршауда емес басқа жағдайларда қарастырады. Солардың ішінде термодинамикалық тепе теңдіктің төрт шартын қарастырайық.

1. Жүйе температурасы тұрақты болатын ортамен қоршалған болсын. Сонымен қатар жүйенің көлемі де тұрақты болсын, мысалы жүйе қатты қоршаумен қоршалған. Бұл жағдайда жүйенің жұмысы барлық уақытта нөлге тең болады, сондықтан шарты орындалады. функциясы тек азаюы немесе тұрақты болуы мүмкін. Осылардан қорыта келе термодинамикалық тепе теңдіктің мынадай шартын тұжырымдауға болады:

Егер қоршаған ортаның температурасы , жүйенің көлемі тұрақты болса және қарастырылып отырған күйде 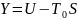функциясы минимал мәнге ие болса, онда жүйенің күйі термодинамикалық тепе теңдікте болады. Егер ортаның температурасы жүйе температурасына тең болса, онда функциясының орнына еркін энергияны қолданамыз, демек .

2. Енді жүйе температурасы мен қысымы үнемі тұрақты болатын ортамен толық қоршалған болсын. Жүйе сыртқы қысымға қарсы жұмыс ғана атқарады, демек жүйенің пайдалы жұмысы үнемі нөлге тең. Сондықтан 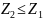шарты орындалады, мұндағы 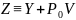функциясы. Егер функциясы жүйенің қандай да бір тепе тең күйінде минимум мәнге ие болса, онда жүйенің тепе теңдігі орнықты болады. Егер жүйенің қысымы сыртқы ортаның қысымына тең болса, онда функциясы жүйенің термодинамикалық потенциалына айналады .

3. Клаузиус теңсіздігін мына түрде жазайық:

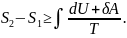
Жүйенің энтропиясы мен көлемі тұрақты болсын. Бұл жағдайда 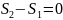және болады, сондықтан Клаузиус теңсіздігін мына түрде жазамыз:

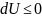Жүйенің температурасы болғандықтан шарты орындалады. Егер көлем мен энтропияны тұрақты ұстап тұрса, онда жүйедегі өздігінен жүретін процестер тек ішкі энергияның кемуімен жүре алады. Егер жүйенің ішкі энергиясы минимал мәнге жетсе, онда жүйеде процестердің жүруі мүмкін болмайды. Бұл қорытындылар тағы бір термодинамикалық тепе теңдік шартын тұжырымдауға мүмкіндік береді. Егер жүйенің көлемі мен энтропиясы тұрақты болып, жүйенің қандай да бір тепе тең күйінде ішкі энергиясы минимал мәнге ие болса, онда жүйенің тепе теңдігі термодинамикалық орнықты болады.

4. Егер жүйенің қысымы мен энтропиясы тұрақты болса және жүйенің қандай да бір күйінде энтальпиясы минимум мәнге ие болса, онда жүйенің тепе теңдігі орнықты болады. Соңғы шартты дәлелдеу үшін Клаузиус теңсіздігін мынадай түрде жазамыз:

Жүйенің қысымы мен энтропиясының тұрақты екендігін ескерсек Клаузиус теңсіздігін мына түрде жаза аламыз:

Жүйенің температурасы болғандықтан 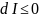шарты орындалады.

§44. Ле-Шателье–Браун принципі

Француз ғалымы Ле-Шателье 1884 жылы және кең мағынада неміс ғалымы Браун 1887 жылы тұжырымдаған термодинамикалық тепе теңдік принципін қарастырайық. Бұл принцип сыртқы әсерден орнықты тепе теңдік күйінен шығарылған жүйедегі процестің өту бағытын алдын ала анықтауға мүмкіндік береді. Ле-Шателье–Браун принципі термодинамиканың екінші бастамасы сияқты жүйенің параметрлерінің сандық мәндерінің өзгерістерін анықтауға мүмкіндік бермейді. Ле-Шателье–Браун принципінің орындалуы үшін сыртқы әсерден тепе теңсіздік күйге көшірілетін жүйенің бастапқы тепе тең күйі орнықты болуы қажет. Ле-Шателье–Браун принципі электродинамикадағы индукциялық токтың бағытын анықтайтын Ленц ережесінің жалпы тұжырымдамасы ретінде тұжырымдалған. Ле-Шателье–Браун принципі: Егер жүйе орнықты тепе тең күйде болса, онда қандай да бір сыртқы әсерден немесе басқа алғашқы процестен туындаған жүйедегі процесс, сыртқы әсер немесе алғашқы процесс тудырған өзгерістерді жоюға бағытталады.

Ле-Шателье және Браун өздері тұжырымдаған жалпы ереженің дербес жағдайлары болып табылатын көптеген мысалдар қарастырып негізінен индуктивтік әдісті қолданған. Алайда олардың берген тұжырымдамасы, әрбір жеке жағдай үшін оңай қолданарлықтай айқын болмады. Ле-Шателье–Браун принципіндегі айқынсыздықтан құтылу үшін және оның дәл математикалық формуласын анықтау үшін §43-та келтірілген шарттарды қолдануға болады.