§41. Энтропияның физикалық мәні. Энтропия және ықтималдылық

1. Больцман гипотезасы.Термодинамиканың екінші бастамасы қайтымсыз процестер барысында жүйенің энтропиясы артып, жүйе тепе-тең күйге жеткенде максимал мәнге жететіндігін көрсетеді. Өз бетімен (табиғи) өтетін барлық жылулық процестер қайтымсыз процестер болып табылады. Жылулық процестердің қайтымсыздығы жүйенің тепе тең күйге өту процесінің басқа өтулерге қарағанда ықтималдығы жоғары екендігін көрсетеді. Сондықтан тәжірибелерде жүйенің ықтималдығы төмен күйден ықтималдығы жоғары күйге өтетіндігін бақылаймыз. Осыдан жүйе тепе тең күйге өткенде энтропияның және ықтималдықтың артатындығын көреміз. Демек, жүйенің қандай да бір күйіндегі энтропиясын сол күйдің ықтималдығымен байланыстыруға болады. Бұл гипотезаны алғаш Л.Больцман енгізген болатын.

Салыстырмалы үлкен флуктуациялар тек аз бөлшектерден тұратын жүйелерде орын алады. Егер тұйық жүйедегі бөлшектер саны өте көп болса, онда жүйе сипаттаушы параметрлері (мысалы, жылдамдықтары) орташа мәннен аз ауытқитын күйде көбірек болады. Бөлшектер саны көп жүйелерде салыстырмалы үлкен флуктуациялар кездеспейді дерліктей, барлық флуктуациялар аз мәндерге ие болады. Тепе-теңдік күйде оң және теріс флуктуациялар тең ықтималдықты. Егер жасанды түрде тепе-теңсіз күй жасалса, онда көбірек жағдайда жүйе ықтималдығы жоғарырақ күйге өтеді. Тұйық жүйедегі өздігінен өтетін процестер кезінде энтропия артатындығы белгілі. Сондықтан жүйенің әрбір күйіндегі энтропиясымен сол күйдің ықтималдығы арасында бірмәнді сәйкестік болуы тиіс. Енді біз осы сәйкестікті анықтайық.

2. Жүйенің ықтималдығы.Енді жүйе күйінің ықтималдығын анықтап алу керек. Мысалы, ыдыс көлемінде газ бөлшектерінің таралуын қарастыруға болады. Ыдыс ішінде 6 молекула болсын және оларды бір бірінен ажырата алу үшін әрқайсысын нөмірлейік. Егер ыдысты ойша екі бөлікке бөліп қарастырсақ, онда ыдыстың екі жағында да молекулалар болады. Молекулалардың ыдыстың екі бөлігіне тарала орналасуының 64 мүмкін әдістері бар. Молекулалардың орналасуының әрбір нұсқасына жүйенің қандай да бір күйі сәйкес келеді. Жүйенің әр күйін қанша әдіспен орындауға болатынын қарастырайық. Мысалы, ыдыстың сол жағында молекула жоқ, ал оң жағында 6 молекула болатын күйді бір ғана әдіспен іске асыруға болады. Сол жағында 1, ал оң жағында 4 молекула болатын күйді алты әдіспен, сол жағында 2, оң жағында 4 молекула болатын күйді 15 әдіспен іске асыруға болады. Ыдыстың екі жағында үш-үштен молекула болатын күйдің әдістер саны ең максимал. Сонымен, егер ыдыс ішіндегі нөмірленген молекуланы ыдыстың екі жағына орналастыру әдістерінің саны 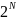болатынына көз жеткіземіз. 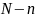Осы барлық орналасулардан ыдыстың бір жағында молекула, ал екінші жағында молекула болатын күйдің орналастырулар саны 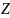мына формуламен анықталады:

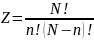(41.1)

Бөлшектер саны қандай болса да орналастыру әдістерінің саны , болғанда максимал мәнге ие болады.Демек, молекулалардың бірқалыпты таралуының орындалу әдістер саны ең үлкені. Ыдысты екіге емес, кез келген бөлікке бөлсек те осы нәтиже шығады.

Ыдыстың бір жағында молекула, ал екінші жағында молекула болатын күйдің орналастырулар санын барлық мүмкін әдістер санына бөлетін болсақ, онда жүйенің сол күйінің ықтималдығын аламыз:

(41.2)

Бұл ықтималдылық та болғанда максимум мәнге ие болады.

Жүйедегі бөлшектер саны көп болған сайын молекулалардың ыдыс ішінде бірқалыпты таралуының мүмкін әдістерінің саны басқа таралуларға қарағанда арта береді. Газ молекулаларының үздіксіз хаосты жылулық қозғалыстарының нәтижесінде жүйе әртүрлі күйлерде болуы мүмкін, бірақ жүйе күйі молекулалардың бірқалыпты таралуына сәйкес күйде болуының ықтималдылығы барлық уақытта жоғары болады.Жүйенің бұл күйі тепе тең күй болып табылады. Егер газ қандай да бір себеппен тепе теңсіздікте болса, онда сыртқы әсерлер болмаса жүйе тепе тең күйге өз бетімен келеді.

Енді осы мысалға ұқсас жағдайды қарастырып көрейік. Бізге көлемі ыдыс берілсін. Осы ыдыстың ішінде молекула болсын. Ыдысты ойша көлемдері болатын бірнеше бірдей бөліктерге бөлейік. Ықтималдықтар теориясына сәйкес ыдыстағы барлық молекулалардың көлемінде болуының ықтималдығы былай анықталады:

(41.3)

Осы мысалдардағы (41.2)және (41.3) формулалармен анықталған ықтималдықтардың мағынасы бірдей. Бірақ біз бірінші жағдайда ықтималдықты жүйенің берілген күйін іске асыру әдістерінің саны бойынша анықтасақ, екінші жағдайда математикалық әдіспен анықтап отырмыз.(41.3) формуласы ыдыстағы барлық молекулалардың көлемінде болу ықтималдығын анықтайды.

3. Больцман формуласы.Больцман гипотезасын іске асыру үшін -ықтималдығы қалай анықталса да оның негізгі жалпы қасиеттерін білу қажет. Энтропия мен ықтималдық арасындағы байланыс универсал болуын талап ету керек, демек бұл байланыс формуласымен өрнектелуі керек. -функциясыбарлық денелер (жүйелер) үшін және олардың кез келген күйі үшін бірдей болуы керек. -функциясының түрін анықтау үшін күйлерінің ықтималдықтары және 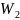болатын екі кіші жүйелерді қарастырамыз. Олардың осы күйлердегі энтропиялары және болсын. Осы екі кіші жүйені бір жүйеге біріктіріп, оның ықтималдығын деп, ал энтропиясын . Осы құрама жүйедегі кіші жүйелер тәуелсіз болғандықтан мына теңдік орындалады ,сондықтан теңдігі де осы жүйе үшін орынды. Сондай-ақ күрделі жүйенің энтропиясы оның құрамындағы кіші жүйелердің энтропияларының қосындысына тең екендігі белгілі:

(41.4)

(41.4)функционалдық теңдеуін шешу үшін және айнымалы ықтималдықтары қалай өзгерсе де олардың көбейтіндісі тұрақты болуын талап етеміз. Сонымен, егер 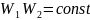болса, онда

. (41.5)

Осы өрнекті дифференциалдасақ

(41.6)

Егер

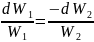(41.7)

шарты орындалса, онда (41.6) теңдеуін (41.7) теңдеуіне мүшелеп бөлсек, мынадай қатынас аламыз:

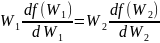(41.8)

(41.8) –өрнектің сол жағында аргументіне тәуелді функция, ал оң жағында аргументіне тәуелді сол функция тұр. және аргументтерінің мүмкін мәндері кез келген болуы мүмкін. Бұдан 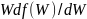функциясы аргументі қалай өзгерсе де тұрақты болатындығы шығады.Бұл тұрақты барлық денелер үшін универсал болуы керек, себебі функциясы универсал екендігін білеміз. Бұл тұрақтыны деп белгілесек, мынадай өрнек аламыз:

,немесе

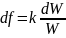
Осыдан функциясы мына түрде анықталады:

Интегралдау тұрақтысы . Осы анықталған шешімді бастапқы (41.4) теңдеуіне қойсақ мынадай өрнек аламыз:

екендігін ескереміз, сонымен

(41.9)

4. -тұрақтысын анықтау. тұрақтысын анықтау үшін тәуелсіз екі әдіспен қандай да бір жүйенің энтропияларын анықтап салыстырамыз. Бір жүйенің кез келген екі күйінің энтропиялар айырымын және сол күйлердің ықтималдықтарының қатынасының логарифмін алу керек. Жүйе ретінде идеал газды қарастырамыз. және бір моль идеал газдың бастапқы және соңғы күйлердегі көлемдері болсын және бұл күйлерде газдың температурасы бірдей болсын. Ықтималдықтардың қатынасын (41.3) формуласын қолданып анықтаймыз. 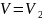Ол үшін бастапқыда көлем , одан кейін деп аламыз. Осылай екі күйдің энтропияларының айырымын мына формуламен анықтаймыз:

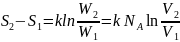
Осы шаманы 37.7 формула бойынша былай анықтаймыз:

Соңғы екі өрнекті салыстырып мынадай өрнек алуға болады:

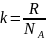(41.10)

Осы анықталған іргелі тұрақты Больцман тұрақтысы болып табылады. Энтропия мен ықтималдықты байланыстыратын (41.9) іргелі қатынасын Больцман алғаш анықтаған және Больцман формуласы деп аталады. Ал осы формуланы келтірілген қорыту әдісін Планк алғаш қолданған. Сондай-ақ тұрақтысын да Планк енгізген болатын.