§40.Термодинамикалық потенциалдар

Термодинамикалық жүйенің күйін сипаттау үшін энтропиямен байланысты басқа да функцияларды қолдануға болады. Жүйе күйінің тәуелсіз параметрлерінің әрбір жиынтығына термодинамикалық потенциалдар сәйкес келеді.Термодинамикалық потенциалдарды қарастырғанда қатынасын пайдаланамыз (мұндағы теңдік белгісі –қайтымды процестер үшін, ал теңсіздік – қайтымсыз процестер үшін).

1. Энтальпия. Егер процесс квазистатикалық болса жәнетұрақты қысым кезінде өтетін болса, онда . Мұндай процесс үшін термодинамиканың бірінші бастамасы мына түрде жазылады:

(40.1)

Бұл теңдеуді мына түрде қайта жазуға болады

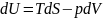(40.2)

Егер жаңа күй функциясы энтальпияны енгізетін болсақ, онда ішкі энергияны энтальпия арқылы өрнектеп мынадай өрнек аламыз:

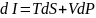(40.3)

Егер екенін ескерсек, онда тұрақты қысымда болады. Бұдан энтальпияның өсімшесі қысым тұрақты болатын квазистатикалық процестегі жүйенің алған жылу мөлшеріне тең екендігі шығады. Сондықтан энтальпияны жылулық функция деп те атайды.(40.3)-теңдеуден энтальпия энтропия мен қысымға тәуелді функция екенін көреміз.

2. Ішкі энергия. Термодинамиканың бірінші бастамасы қайтымды процесс үшін: . Мұнда U- потенциалы үшін айнымалылар энтальпия S және V көлем болып табылады. Олай болса,

,

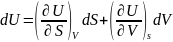(40.4)

3. Еркін энергия. өрнегі бойынша қайтымды изотермиялық процесс кезінде атқарылатын жұмыс

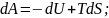
Жүйеде өтіп жатқан процесс изотермиялық екенін ескеріп былай жаза аламыз:

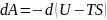(40.5)

Енді еркін энергия деп аталатын тағы бір термодинамикалық функцияны енгізуге болады:

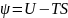(40.6)

Бұл функцияны алғаш Гельмгольц енгізген болатын. Егер бұл функцияны дифференциалдасақ, онда

(40.7)

Термодинамиканың бірінші бастамасын және процестің изотермиялық екенін ескерсек, онда еркін энергия үшін мынадай өрнек аламыз:

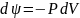немесе 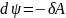, (40.8)

демек,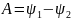 .Сонымен, еркін энергия –кемуі квазистатикалық изотермиялық процесс кезінде жүйенің атқарған жұмысына тең болатын күй функциясы. Еркін энергия Т температура мен Vкөлемнің функциясы болып табылады.

4. Гиббстің термодинамикалық потенциалы.Термодинамикада тағы бір потенциал қолданылады. Оны алғаш рет Гиббс енгізген болатын. Гиббстің термодинамикалық потенциалы:

немесе

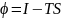
және

(40.9)

түрде жазуға болады. Егер Гиббс потенциалын дифференциалдасақ, онда

бұдан

(40.10)

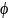5.Зат күйінің канондық (Гиббс) теңдеулері.(40.2), (40.3), (40.7) және (40.10) қатынастарынан ішкі энергия энтропия мен көлем функциясы, энтальпия – мен функциясы, еркін энергия – мен функциясы, ал термодинамикалық функция – мен функциясы екендігін көруге болады. Демек,

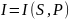, , , (40.11)

Бұл қатынастар зат күйінің канондық теңдеулері деп аталады. Бұл теңдеулерді термодинамикаға Гиббс жүйелі түрде енгізген болатын. Канондық теңдеулердің әрқайсысы зат қасиеттері туралы термиялық немесе калориялық теңдеулерге қарағанда көбірек мағлұмат беретіндігін Гиббс атап көрсеткен. (40.11) төрт теңдеудің кез келгені заттың термиялық және калориялық қасиеттері туралы толық мағлұматқа ие. (40.11) теңдеулерден мынадай қатынастар алуға болады:

, ,

, .

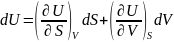Бұлқатынастарды (40.2), (40.3), (40.7) және (40.10) қатынастарымен салыстырудан мынадай формулалар аламыз:

, , (40.12)

, , (40.13)

, , (40.14)

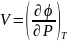, . (40.15)

6. Гиббс-Гельмгольц теңдеулері.Осы алынған қатынастардан шығатын екі салдарды қарастырайық. және функцияларының анықтамасынан , екендігі шығады. Осы қатынастарға (40.14) және (40.15) формулаларынан энтропия өрнегін қоятын болсақ, мынадай теңдеулер аламыз:

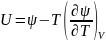, (40.16)

. (40.17)

Осы теңдеулер Гиббс Гельмгольц теңдеулері деп аталады.

7. Максвелл қатынастары. (40.12) теңдеулерден екінші ретті дифференциал алайық:

, .

Осыдан дифференциалдаудың ретін өзгерту теоремасы негізінде былай жазуға болады:

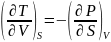. (40.18)

Осы әдіспен (40.13) -(40.15) теңдеулерінен мынадай қатынастар алуға болады:

, (40.19)

, (40.20)

. (40.21)

Осы қатынастар Максвелл қатынастары деп аталады. Бұл қатынастар жүйелердің термодинамикалық тепе тең күйлерін сипаттайтын шамалардың арасындағы қатынастарды анықтау үшін қолданылады. Бұл әдіс термодинамикалық функциялар немесе термодинамикалық потенциалдар әдісі деп аталады.