§32. Жіңішке саңлаудан шыққан газдың жылдамдығы

С ығылған газдың ыдыстан жіңішке саңлаудан шыққандағы жылдамдығын анықтайық. Газ ағынын ламинарлы және тұрақталған деп ескеріп, бір ұшы (2) ыдыстың сыртында, екінші ұшы (1) ыдыс ішінде болатын ағыс сызығын қарастырайық (25-сурет). Ыдыс ішіндегі газдың жылдамдығы өте аз деп ескереміз.Осы ағыс сызығындағы 1 және2 нүктелер үшін Бернулли теңдеуін жазайық:

жылдамдығын ескермейміз және 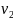жылдамдығының индексін алып тастасақ, онда

(32.1)

Бұл формула идеал газ үшін де нақты газ үшін де жарамды. Газды идеал деп ескеріп және жылусыйымдылықтың температураға тәуелділігін ескермесек, онда энтальпияны мына түрде жаза аламыз:

,

Егер Роберт Майер теңдеуін ескерсек, онда

(32.2)

Енді (32.1) өрнекті мына түрде жаза аламыз:

(32.3)

Бұл формуланы практикада қолдану ыңғайсыз, себебі ыдыстың сыртындағы 2 нүктедегі газ ағынының температурасын өлшеу өте қиын. Сондықтан, адиабата теңдеуінен осы температураны анықтау керек. Ыдыс ішіндегі газдың температурасы , қысымы және сыртқы ортаның қысымы белгілі. Процесс адиабаталық болғандықтан:

,

бұдан

.

температурасы үшін алынған өрнекті (32.3) формулаға қойып мынадай формула аламыз:

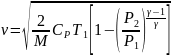. (32.4)

Бұл формуладан газ ағынының жылдамдығы қоршаған орта вакуум болғанда максимал болатындығын көрсетеді:

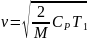.(32.5)

Егер сыйымдылығын адиабата тұрақтысы арқылы өрнектесек , онда мынадай өрнекке келеміз:

, (32.6)

мұндағы -дыбыс жылдамдығы.

Бақылау сұрақтары:

1. теңдеуі газдың қандай ағысы үшін орындалады?

2. Сығылған газдың ыдыстан жіңішке саңлау арқылы шығу жылдамдығын қорытып шығарыңыз.

3. Сығылған газдың ыдыстан жіңішке саңлау арқылы шығуы қандай процессте өтеді?

4.Термодинамиканың екінші бастамасы

1. Термодинамиканың бірінші бастамасы өтіп жатқан термодинамикалық процестің бағыты туралы ешқандай мағлұмат бермейді. Термодинамиканың бірінші бастамасы оқшауланған жүйенің энергиясы тұрақты болып қалуын талап етеді. Егер адиабаталық оқшауланған жүйе екі денеден тұратын болса, онда олардың арасындағы жылу алмасу шартын қанағаттандырады. Мұндағы бірінші дененің екіншісінен алған жылу мөлшері, ал 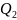екінші дененің біріншіге берген жылу мөлшері. Жылу қай бағытта өтетіндігін термодинамиканың бірінші бастамасы түсіндірмейді.

Термодинамиканың екінші бастамасы процестің бағытын айқын көрсетеді. Екінші бастама температураның сандық мөлшерін анықтауға және рационалды температура шкаласын жасауға мүмкіндік береді.

2.Термодинамиканың екінші бастамасының негізін салған француз инженері және физигі Сади Карно. Өзінің 1824 жылы жарық көрген «Оттың қозғалтушы күші және сол күшті тудыратын машиналар туралы» деген еңбегінде Карно жылуды жұмысқа айналдыру шарттарын зерттеген. Бірақ ол кезде Карно жылутегі көзқарасында болғандықтан термодинамиканың нақты тұжырымдамасын бере алмады. 1850-51 жылдары бір-бірінен тәуелсіз неміс ғалымы Рудольф Клаузиус пен шотланд физигі Вильям Томсон (лорд Кельвин) термодинамиканың екінші бастамасын тұжырымдады.

3. Қыздырғыш пен суытқыш.Жылулық (ішкі) энергиясының қоры бар денелер жылу резервуары деп аталатыны белгілі. Егер қарастырылатын жүйенің күйін жанастыру арқылы өзгертуге берілген екі жылу резервуаларының бірінің температурасы , ал екіншісі болса және қатынасы орындалса, онда бірінші резервуарды қыздырғыш, ал екінші резервуарды суытқыш ретінде қолдануға болады.

Бақылау сұрақтары:

1. Термодинамиканың бірінші бастамасы өтіп жатқан термодинамикалық процестің бағытын анықтайды ма?

2. Жылу резервуары деп нені айтамыз?

3. Қыздырғыш пен суытқыш қалай таңдалады?