§31. Бернулли теңдеуі*

1. Бернулли теңдеуі идеал сұйықтың ламинарлы стационар ағысын сипаттайды. Мұнда сұйық ұғымы жалпы мағынаға ие, сондықтан газды сығылатын сұйық ретінде қарастыруға болады. Сұйықтың идеалдығы гидродинамикалық мағынада беріледі, демек сұйықтың қозғалысы қандай болса да оның ішінде тұтқырлық күшінің тангенциал құраушысы болмауы керек және сұйықтың қабаттасатын элементтері арасындағы әсерлесу қысымның нормаль күші есебінен болуы керек. Сондай-ақ сұйықтың бөліктері арасындағы жылу алмасуды ескермейміз. Сұйықтың қозғалатын бөлігі үшін қалған бөлігі адиабаталық қоршау ролін атқарады. Сондықтан біз сығылатын идеал сұйықтың адиабатты ламинарлы ағысын қарастырамыз.

2. Қозғалыстағы сұйықты термодинамикалық тепе-теңдіктегі жүйе ретінде қарастыруға болмайды. Егер сұйықтың макроскопиялық қозғалысының жылдамдығы кеңістік және уақыт бойынша өте тез өзгермейтін болса, онда сұйықты жеткілікті аз макроскопиялық бөліктерге бөлуге болады. Осы бөліктер барлық сұйық сияқты жылдамдыққа ие болады, ал оның ішкі күйітермодинамикалық тепе-теңдік күйіндегідей параметрлермен сипатталады. Бұл параметрлер күй теңдеуімен 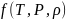байланысқан, сондай-ақ олардың арасында ағыстың адиабаттылығын өрнектейтін қосымша байланыс орын алады. Идеал газ үшін адиабаттылық шарты өрнегімен сипатталады.Барлық жағдайда адиабаттық ағыс кезінде, күй теңдеуімен байланысқандықтан 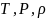үш параметрінің бірі тәуелсіз болады, мысалы, газ тығыздығы.

3.Идеал сұйықтың стационар ламинарлы ағысы үшін ағыс сызығы бойында Бернуллитеңдеуі орындалады:

(31.1)

Бұл теңдеудегі сұйықтың масса бірлігінің толық энергиясы болып табылады және үш құрамдас бөлігі бар: макроскопиялық қозғалыстың кинетикалық энергиясы – 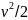;сыртқы күш өрісіндегі потенциалдық энергия – ; ішкі энергия – . Егер сыртқы күш өрісі ауырлық күшінің өрісі болса, онда , мұндағы -таңдалған деңгейден есептелетін биіктік. Осыларды ескерсек, онда Бернулли теңдеуі мына түрге келеді:

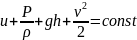(31.2)

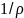шамасы сұйықтың меншікті көлемі, сондықтан 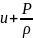меншікті энтальпия болып табылады, демек сұйықтың масса бірлігінің энтальпиясы. Осыны ескеріп және меншікті энтальпияны деп белгілеп Бернулли теңдеуін мына түрде жаза аламыз:

(31.3)

Егер сұйықтың ағысы горизонталь бағытта болса, онда тұрақты болады. Бұл жағдайда:

(31.4)

Ағыс жылдамдығының үлкен мәндерінде ағыс сызығы горизонталь болмаса да осы теңдеуді қолдануға болады. Себебі потенциалдық энергияның биіктік бойынша өзгерісін, кинетикалық энергиямен салыстырғанда елемеуге болады.

Егер горизонталь сызық бойымен аққан сұйықтың жылдамдығы өте баяу болса, онда кинетикалық энергияны да елемеуге болады. Бұл жағдайда Бернулли теңдеуі мына түрге келеді:

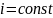, (31.5)

демек энтальпия ағыс сызығы бойында тұрақты болады. Осындай нәтижені Джоуль-Томсон тәжірибесін қарастырғанда да алған едік.

Бақылау сұрақтары:

1. Қозғалыстағы сұйық термодинамикалық тепе-теңдікте бола ма?

2. Идеал газ үшін адиабаттылық шартын көрсет?

3. Меншікті энтальпия өрнегін жазып көрсетіңіз.

4. Бернулли теңдеуін қорытып шығарыңыз.