§29. Клеман және Дезорм әдісімен қатынасын анықтау*

Клеман (1179-1842) және Дезорм (1777-1862) 1819 жылы газдар үшін жылусыйымдылықтар қатынасын өлшеудің әдісін ұсынды. Сыйымдылығы бірнеше литр болатын шыны баллон атмосфералық қысымда ауамен толтырылады (24-сурет). Сорғыштың көмегімен баллонға тағы да ауаның біраз мөлшері толтырылып, краны жабылады. Аз уақыттан соң баллондағы газдың температурасы қоршаған орта температурасымен теңескен соң оның қысымы сұйықтық манометрмен өлшенеді.Ауаның бұл қысымын , ал температурасын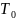 деп белгілейміз. Енді кранын аз уақытқа ашып, баллондағы газ қысымын атмосфералық қысыммен теңестіреміз, сонда баллондағы қысым болады. Бұл кезде баллондағы газ адиабатты ұлғайып, сыртқы ауаның қысымына қарсы жұмыс атқарады. Сондықтан оның температурасы белгілі бір шамаға азаяды. Осы қысқа процесс барысында краны ашық болады. Содан кейін краны тез жабылып баллондағы газдың температурасы қоршаған ауа температурасымен теңеседі, ал қысымы болады. Осылай өлшенген , , қысымдар бойынша жылусыйымдылықтар қатынасы анықталады.

Ол үшін ыдыс ішінде ойша тұйық бетпен (қабықшамен) шектелетін газдың мөлшерін қарастырамыз. 24-суретте бұл көлем штрихталған қисықпен көрсетілген. Газдың әртүрлі процестерінде осы қабықша ішіндегі газ ұлғайып, сығылып қоршаған газға қарсы жұмыс атқарады және онымен жылу алмасады. Бұл процестер квазистатикалық болып табылады, себебі макроскопиялық қозғалыстың кинетикалық энергиясы өте аз. Сипатталған процестер кезіндегі қабықша ішіндегі газдың күйі сәйкес өзгеріп отырды деп ескереміз. Мысалы, 1-күйде – , 2-күйде – , ал 3-күйде – . Газ 1-күйден 2-күйге адиабатты өтеді, сондықтан бұл күйлер үшін адиабата теңдеуін жазамыз:

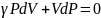
Мұндағы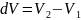 , ал . Осыны ескерсек:

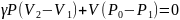(29.1)

1-күймен 3-күйдегі температуралар бірдей, демек бұл күйлер үшін теңдігі орындалады. Олай болса 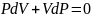, немесе

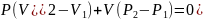. (29.2)

(29.1), (29.2) қатынастарын бірге шешсек, онда

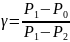. (29.3)

Бұл теңдеу бойынша қысымдар айырымдарының қатынасы түрінде анықталады. Сондықтан қысымды кез келген бірлікте өлшеуге болады. Тәжірибеде ыңғайлысы қысымды су бағанының биіктігімен (миллиметр) өлшеген.

Бақылау сұрақтары:

1. Клеман және Дезорм әдісін сипаттаңыз.

2. Клеман және Дезорм тәжірибесінде газда қандай процесс орын алады?

3. Клеман және Дезорм әдісінде шамасы қандай параметрлер арқылы анықталады?

§30. Газдардағы дыбыс жылдамдығы*

1. Ньютон формуласы.Механика курсында газдардағы дыбыстың таралу жылдамдығы үшін мынадай формула қорытылып шығарылады:

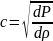, (30.1)

мұндағы -газдың тығыздығы. Газдың қысымы тек тығыздыққа ғана емес, температураға да тәуелді. Сондықтан туындысын қандай мағынада түсіну керек екендігін білген дұрыс. Ньютон қысым мен тығыздық Бойль-Мариотт заңымен 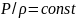байланысқан деп ескерді. Дыбыс ортада таралғанда ауаның тығыздалған және сиреген нүктелеріндегі температура бірдей болады, демек дыбыстың газда таралуы изотермиялық процесс. Олай болса, бұл туындыны былай түсінген дұрыс: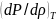 . Онда (30.1) формуласы Ньютон формуласына айналады:

, (30.2)

мұндағы 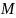-газдың мольдік массасы, ал индексі дыбыс жылдамдығы Ньютон формуласымен есептелгенін көрсетеді. Енді осы формула көмегімен мольдік массасы 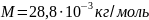, температурасы болатын ауадағы дыбыс жылдамдығын анықтайық. , ал тәжірибеде .

2.Лаплас формуласы.Тәжірибе мен теория арасындағы алшақтықты Лаплас (1749-1827) ескерді. Лапластың пайымдауынша дыбыс толқынындағы тығыздық пен температураның өзгерісі өте жылдам өтеді, ауаның жылу өткізгіштігі өте аз, демек мұндай процестер үшін жылу алмасудың ролі жоқ. Дыбыс толқынындағы ауаның тығыздалған және сиреген нүктелеріндегі температура тепе-теңдікке келіп үлгермейді, сондықтан дыбыстың таралу процесін адиабатты процесс деп ескеруге болады. Олай болса бұл процесс үшін изотерма теңдеуін емес адиабата теңдеуін қолдану керек. Егер адиабата теңдеуіндегі көлемді тығыздық арқылы өрнектесек, онда адиабата теңдеуін мына түрде жаза аламыз:

,(30.3)

Бұдан

.(30.4)

Осы теңдеуден Лаплас теңдеуін аламыз:

.(30.5)

Бұл теңдеу Ньютон формуласымен есептелген жылдамдыққа қарағанда 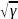есе көп жылдамдықты береді. Ауа үшін . Лаплас формуласына сәйкес температурасы ауадағы дыбыс жылдамдығы:

.

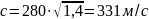Лаплас формуласымен анықталған ауадағы дыбыс жылдамдығының мәні тәжірибелік мәнімен өте жақсы дәл келеді.

3. қатынасын анықтау әдісі. Ньютон және Лаплас формулаларына жылусыйымдылықтардың қатынасын тұрақтысын анықтаудың тағы бір эксперименттік әдісі негізделген. Бұл әдіс Клеман-Дезорм әдісіне қарағанда дәлдігі жоғарырақ әдіс болып табылады. Экспериментте зерттелетін газдағы дыбыс жылдамдығы ( ) өлшенеді. Ал -ның мәні мына формула бойынша есептеледі:

, (30.6)

мұндағы 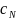-Ньютондық дыбыс жылдамдығы, -экспериментте анықталған дыбыс жылдамдығы.

Бақылау сұрақтары:

1. Газдардағы дыбыс жылдамдығы Ньютон формуласымен қалай анықталады?

2. Ньютон формуласын қорытып шығарғанда газда қандай изопроцесс орындалатыны ескерілуі керек?

3. Лаплас газда дыбыс таралғанда қандай процесс орындалады деп есерген?

4. Лаплас теңдеуін қорытып шығар.

5. Лаплас теңдеуімен анықталған дыбыс жылдамдығы Ньютон формуласымен анықталған жылдамдықтан қанша есе көп?