
- •1. Температура
- •§1. Температура және термодинамикалық тепе-теңдік
- •§2 Термоскоп және температуралық нүктелер
- •§3 Температура шкалалары
- •2. Идеал газдың молекула-кинетикалық теориясы
- •§4.Идеал газ
- •§5. Газ қысымы. Молекула-кинетикалық теорияның негізгі теңдеуі
- •§6. Идеал газ күйінің теңдеуі
- •§7. Идеал газ заңдары
- •§8. Орташа квадраттық жылдамдық
- •Бақылау сұрақтары:
- •§9. Барометрлік формула
- •Бақылау сұрақтары:
- •§10. Больцман таралуы
- •§11. Ықтималдықтар теориясынан қысқаша түсінік
- •§12. Кездейсоқ шаманың орташа мәні. Ықтималдықтардың таралу функциясы
- •§13. Жүйенің макроскопиялық және микроскопиялық күйлері
- •§14. Макрокүйдің ықтималдығы
- •§15. Канондық ансамбль. Гиббс таралуы
- •§16. Газ молекулаларының жылдамдықтары бойыншатаралуының Максвелл заңы
- •§17. Молекулалардың жылдамдықтың абсолюттік мәні бойынша таралуы. Молекулалардың орташа жылдамдықтары
- •§18. Перрен тәжірибесі
- •3. Термодинамиканың бірінші бастамасы
- •§19. Квазистатикалық процестер
- •§20. Макроскопиялық жұмыс
- •§21. Термодинамиканың бірінші бастамасы
- •§22. Ішкі энергия
- •§23. Жылу мөлшері
- •§24. Жылусыйымдылық
- •§25. Идеал газдың ішкі энергиясы. Джоуль заңы
- •§26. Адиабаттық процесс. Пуассон теңдеуі
- •§27. Газ көлемінің адиабаталық өзгерісі кезіндегі жұмыс
- •§28. Политроптық процесс
- •§29. Клеман және Дезорм әдісімен қатынасын анықтау*
- •§30. Газдардағы дыбыс жылдамдығы*
- •§31. Бернулли теңдеуі*
- •§32. Жіңішке саңлаудан шыққан газдың жылдамдығы
- •4.Термодинамиканың екінші бастамасы
- •§33. Қайтымды және қайтымсыз процестер
- •§34. Термодинамиканың екінші бастамасының әр түрлі тұжырымдамалары
- •§35. Карно циклі
- •§36. Температураның термодинамикалық шкаласы
- •§37 Клаузиус теңсіздігі. Энтропия
- •§38. Энтропияның өсу заңы
- •§39. Газдардың диффузиясы кезінде энтропияның өсуі. Гиббс парадоксі
- •§40.Термодинамикалық потенциалдар
- •§41. Энтропияның физикалық мәні. Энтропия және ықтималдылық
- •§42. Нернст теоремасы
- •§43. Термодинамикалық тепе теңдік шарттары
- •Газдардағы тасымалдау құбылыстары
- •§44. Еркін жүрудің орташа жолы
- •Нақты газдар
- •§47 Беттік керілу
- •§48Шектік бұрыштар. Жұғу және жұқпау
- •§49. Сұйықтың майысқан бетінің екі жағындағы қысымдар айырымы. Лаплас формуласы
- •§50. Фазалар және фазалық түрленулер
§27. Газ көлемінің адиабаталық өзгерісі кезіндегі жұмыс
Өткен тақырыптағы (§26) адиабата теңдеуін қолданып газдың адиабаталық ұлғаюы немесе сығылуы кезіндегі жұмысты табуға болады.
1 моль газдың адиабаталық
ден
-ге
дейін ұлғаюы кезіндегі жұмысын анықтайық.
Газ көлемі
-ға
өзгергенде элементар жұмыс былай
анықталады:
моль газдың адиабаталық
ден
-ге
дейін ұлғаюы кезіндегі жұмысын анықтайық.
Газ көлемі
-ға
өзгергенде элементар жұмыс былай
анықталады:
Газ қысымы мен көлемі арасындағы байланыс адиабата теңдеуімен анықталады.Процесс квазистатикалық болуы үшін, ұлғаю адиабата бойымен жүруі керек (23-сурет) :
Бұл теңдеуді мына түрде жазуға болады:
 ,
,
мұнда -газдың бастапқы қысымы, бастапқы көлемі. Бұдан
 .
.
Қысымның осы өрнегін жұмыстың формуласына қойып, мынадай өрнек аламыз:
 .
.
Жұмысты анықтау үшін осы өрнекті ден -ге дейінгі аралықта интегралдаймыз:
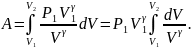
Осы өрнектегі интеграл былай анықталады:

Күй
теңдеуінен
 екенін
ескерсек, онда жұмысты мына түрде
анықтаймыз:
екенін
ескерсек, онда жұмысты мына түрде
анықтаймыз:
 .(27.1)
.(27.1)
(26.5)
теңдеуге сәйкес болғандықтан
болғандықтан
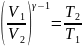 .
Сондықтан, көлем адиабатты ұлғайғанда
жұмысты мына түрде де анықтауға болады:
.
Сондықтан, көлем адиабатты ұлғайғанда
жұмысты мына түрде де анықтауға болады:
 (27.2)
(27.2)
Соңғы
формулада
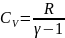 екендігі ескерілген.
екендігі ескерілген.
Сонымен, адиабаттық ұлғаю кезінде газ изотермиялық ұлғаю кезіндегіге қарағанда аз жұмыс атқаратындығын анықтадық. Адиабаттық ұлғаю кезінде атқарылған жұмыс 23-суреттегі штрихталған ауданға тең болады.
Бақылау сұрақтары:
Адиабатты ұлғайған газдың жұмысын анықтаңыз.
Адиабатты ұлғайған газдың жұмысы мен изтермиялы ұлғайған газдың жұмысын салыстырыңыз.
Роберт Майер теңдеуін және қатынасын қолданып және жылусиымдылықтарын және
 арқылы өрнектеңіз.
арқылы өрнектеңіз.
§28. Политроптық процесс
Біз қарастырған газ күйінің өзгеруінің изотермиялық және адиабаталық процестеріидеалданған процестер болып табылады. Изотермиялық процесс кезінде жүйенің қоршаған ортамен немесе термостатпен идеалды жанасуы талап етілсе, адиабаталық процесс кезінде жүйенің қоршаған ортадан идеалды оқшаулануы талап етіледі. Бұл екі процесті политроптық процесс деп аталатын жалпы процестің дербес жағдайлары деп қарастыруға болады.
Егер
термодинамикалық процестер кезінде
газдың жылусыйымдылығы тұрақты болып
қалса, онда мұндай процесс политроптық
процесс деп аталады. Кез келген политроптық
процесс үшін
 .
.
Политроптық процессті сипаттайтын политропа теңдеуін анықтайық. Термодинамиканың бірінші бастамасына сәйкес
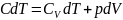 ,
,
бұл теңдеуді ықшамдасақ
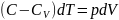 .
(28.1)
.
(28.1)
Идеал газ күйінің теңдеуінен -ны өрнектейміз (§26қара):
 .
.
Бұл
өрнекті (28.1) өрнегіне қойып және
 екенін
ескеріп мынадай өрнек аламыз:
екенін
ескеріп мынадай өрнек аламыз:
 .
.
Бұл өрнекті ықшамдап мынадай өрнек аламыз:
 .
.
Осы өрнекті тағы да ықшамдап, айнымалыларды бөсек, онда мынадай дифференциалдық теңдеу аламыз:
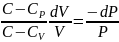 .
.
Теңдеудің сол жағындағы жылусыйымдылықтар айырымдарының қатынасын былай белгілейік:
 (28.2)
(28.2)
Енді алған теңдеуді интегралдап
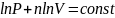 .
.
Осы теңдеуді потенцирлеу арқылы политроптық процестің теңдеуін аламыз:
 .
(28.3)
.
(28.3)
Политроптық процесс теңдеуіндегі (28.2) өрнекпен анықталатын политропа көрсеткіші деп аталады.
Политроптық
процесс барлық изопроцестер және
адиабаталық процесс үшін жалпы теңдеу
болып табылады. Егер
болса, онда ,
,
 болады, демек адиабаталық процесс болып
табылады. Изотермиялық процесте
болады, демек адиабаталық процесс болып
табылады. Изотермиялық процесте
 ,
демек
,
демек
 ,
онда
,
,
онда
,
 болады.
Изобаралық процесс кезінде
болады.
Изобаралық процесс кезінде
 ,
демек
,
демек
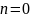 ,
онда
.
Егер
,
онда
.
Егер
 болса, онда
болса, онда
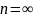 және
болады, демек изохоралық процесс
орындалады.
және
болады, демек изохоралық процесс
орындалады.
Бақылау сұрақтары:
Қандай процесті политроптық процесс деп атайды?
Политропа көрсеткіші қалай анықталады?
Политроптық процесті сипаттайтын теңдеуді қорытып шығарыңыз.
, , , болатын процестерді талдап көрсетіңіз.
