§17. Молекулалардың жылдамдықтың абсолюттік мәні бойынша таралуы. Молекулалардың орташа жылдамдықтары

1.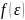 -функциясы газдың нүктелік молекулалары жылдамдықтар кеңістігінде таралуы кезіндегі ықтималдылықтың көлемдік тығыздығын сипаттайды. Егер -функциясын барлық молекулалар санына (N) көбейтсек, онда жылдамдықтар кеңістігінің бірлік көлеміндегі молекулалардың ықтимал санын анықтаймыз.

Енді газ молекулаларының жылдамдықтарының абсолют мәндері бойынша таралуын анықтайық. Жылдамдық бағыттарын енді ескермейміз. Молекула жылдамдығының модулі интервалында жату ықтималдығын табу керек. Бұл ықтималдықты 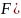)d деп белгілейміз. Осы ықтималдықты барлық молекулалар санына көбейтсек, онда осындай жылдамдыққа ие болатын молекулалардың ықтимал санын dNаламыз. Жаңа таралу функциясы )алғашқы енгізілген ( ) функциясымен қарапайым байланысқан. Бір нүктеден барлық молекулалардың жылдамдық векторларын саламыз. Олардың ішінен жылдамдығы интервалында жататын векторларды іріктеп аламыз. Сәйкес жылдамдық нүктелері орташа радиусы қалыңдығы болатын шар қабықшасын құрайды. Бұл қабықшаның көлемі болады. Шар қабықшасының ішіндегі көлемдік тығыздық тұрақты болады. Себебі, тек қана жылдамдықтың модуліне тәуелді, ал бағытына тәуелді емес. ункциясын осы қабықша көлеміне көбейтіп іздеп отырған ықтималдықты табуға болады:

(17.1)

Осы ықтималдықты біз белгілегенбіз. Осы өрнектерді салыстырып

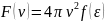(17.2)

екеніне көз жеткіземіз. Сонымен

(17.3)

Демек,

(17.4)

Әрине, функциясы нормирлеу шартын қанағаттандыруы керек,

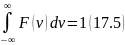
2 . фунциясының графигі 13-суретте келтірілген. қисығы ассиметриялы, коорлината басында нөлге тең. функциясы керісінше симметриялы және координата басында максимум мәнге ие екендігін білеміз. Неге мұндай айырмашылық болатынын анықтайық. өрнегі молекуланың және 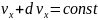жазықтықтарының арасындағы өте жұқа қабатта болу ықтималдығын анықтайды. өрнегі де молекулалардың осындай жазықтықтар арасындағы жұқа қабатта болу ықтималдығын анықтайды. Ерекшелігі сфералық жазықтықтар арасындағы жұқа қабатта болу ықтималдығын көрсетеді. Бірінші жағдайда пен тұрақты мәндерінде жазық қабаттар бірдей болады. Сондықтан өрнегі және функциясы 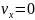болғанда максимум мәнге ие болады. Керісінше, сфералық қабаттардың көлемі жылдамдық артқан сайын өседі, себебі . Сондықтан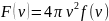 функциясының максимумы функциясы мен көбейтіндісімен анықталады.

3. функциясы максимумге ие болатын жылдамдық ең ықтимал жылдамдық деп аталады. Оны депбелгілейік. жылдамдығын анықтау үшін -функциясын аргументі арқылы қарастыру керек.

(17.6)

Осы функцияны аргументі бойынша дифференциалдап нөлге теңестірсек функциясының максимум мәніне сәйкес келетін аргумент мәнін аламыз:

;

,

,

,

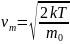.(17.7)

Молекулалардың орташа арифметикалық жылдамдығы былай анықталады:

Осы өрнекке функциясын қойып интегралдасақ:

.(16.8)

Енді орташа квадраттық жылдамдықты анықтайық. Молекулалардың ілгерілемелі қозғалысының кинетикалық энергиясы , ал молекула-кинетикалық теорияның негізгі теңдеуіне сәйкес бұл энергия – . Сондықтан,

,

Бұл өрнектен жылдамдықты анықтасақ,

.(17.9)

Сонымен, газ молекулаларының ең ықтимал, арифметикалық орташа және орташа квадраттық жылдамдықтарды салыстырайық.

– ең ықтимал жылдамдық, –арифметикалық орташа жылдамдық және – орташа квадраттық жылдамдық. арифметикалық орташа және орташа квадраттық жылдамдықтарды ең ықтимал жылдамдық арқылы өрнектесек мынадай қатынастарды алуға болады:

;

Осы үш жылдамдықтардың бір-бірінен айырмасы шамасы бірге тең көбейткіш болып табылады және олардың шамалары өзара қатынаста болады. Сондықтан бұл жылдамдықтардың кез келгенін молекулалардың жылулық қозғалысын сипаттау үшін қолдануға болады. .

Бақылау сұрақтары:

1. функциясы функциясы арқылы қалай анықталады?

2. функциясының графигін түсіндір.

3. Ең ықтимал жылдамдық деп қандай жылдамдықты айтамыз және ол қалай анықталады?

4. Арифметикалық орташа жылдамдық қалай анықталады?

5. Орташа квадраттық жылдамдықты таукып көрсет.