§15. Канондық ансамбль. Гиббс таралуы

1. Жылдамдықтық және энергиялық микрокүйлер.Біз негізінен бөлшектердің жылдамдық бойынша микрокүйлерін талдауды қажет етпейтін микроканондық ансамблдерді қарастырдық. Себебі, тепе-теңдік күйде бөлшектердің жылдамдық бойынша микрокүйлер саны бірдей болды және толық энергияның тұрақты болу шартын қанағаттандыратын микрокүйлер саны максимал болды.Микрканондық ансамблдердің қасиеттерін анықтауға эргодикалық гипотеза мен теңықтималдылық принциптері негіз болды.

Енді бөлшектердің микрокүйлерінің жылдамдықтар бойынша таралуын қарастырамыз. Қандай да бір бөлшекті таңдап оның жылдамдығын әртүрлі уақыт мезеттерінде ансамблдегі бір жүйеде, сондай-ақ ансамблдің әртүрлі жүйелерінде бір уақыт мезетінде қарастырамыз. Бөлшектердің жылдамдықтарын білу олардың кинетикалық энергиясы туралы толық мағлұмат береді. Бөлшектің жылдамдығы мен кинетикалық энергиясы басқа бөлшектермен соқтығысқанда өзгереді. Сонымен бөлшек ансамблдің әртүрлі жүйелерінде жылдамдық және энергиясы бойынша әртүрлі күйлерде болады. Егер жүйелердің біріндегі бөлшекті бақылайтын болсақ, онда уақыт өтуіне байланысты оның жылдамдық пен энергия бойынша күйі өзгеріп отырады. Жылдамдық пен энергия бойынша микрокүйлерді анықтау негізгі мәселе болып табылады.

2. Канондық ансамбль анықтамасы.Қарастырылатын жүйе болып табылатын бөлшектің жылдамдығының және энергиясының микрокүйін қарастырайық. Бұл жүйе оқшауланбаған, себебі ол бірге тұйық жүйе құрайтын басқа бөлшектермен энергия алмастырады. Оқшауланған жүйелерден тұратын жүйе микроканондық жүйе деп аталады. Ал, сәйкес оқшауланбаған жүйелерден тұратын жүйе канондық ансамбль деп аталады. Сонымен, канондық ансамблдегі әрбір жүйе үлкен оқшауланған жүйенің бір бөлігі болып табылады. Канондық ансамблдегі әрбір жүйе оның кеңістіктік мағынадағы бөлігі емес, энергия және жылдамдық бойынша күйлері мағынасындағы бөлігі. Кеңістіктік мағынада бұл бөліктің өлшемі бүкіл жүйенің өлшемімен бірдей болуы мүмкін. Канондық ансамблдің әрбір жүйесінде бір немесе көптеген бөлшектер болуы мүмкін, әрбір жүйедегі бөлшектер саны үлкен жүйедегі бөлшектер санынан аз болуы маңызды. Канондық ансамблдегі жүйелердің энергиялары әртүрлі болуы мүмкін. Мәселе канондық ансамблдегі жүйелердің әртүрлі энергиялық күйлерінің ықтималдылығын табуға тіреледі. Бұл мәселені шешу канондық ансамбль құрамындағы жүйенің барлық күйлері туралы толық ақпарат береді, себебі бірдей энергиялы күйлер жиынтығы микроканондық ансамблді құрайды. Канондық ансамбль құрамындағы жеке жүйе канондық жүйе болып табылады. Канондық ансамблдегі жүйенің энергияларын талдағанда, канондық ансамбль анықтамасына сәйкес, тек қана кинетикалық энергия ғана емес, потенциалдық энергия да қарастырылады.

3. Гиббс таралуы немесе канондық таралу. Канондық жүйені ыңғайлы болуы үшін кіші жүйе деп, ал құрамында осы кіші жүйе болатын жүйені – жүйе деп атаймыз. Жүйе микроканондық ансамблге жататынын және оның тұрақты толық энергиясы болатынын еске түсірейік. Кіші жүйенің энергиясы , ал жүйенің қалған бөлігінің энергиясы болсын. Кіші жүйенің бұл күйі нақты микрокүйлердің бірі болып табылады. Сонымен қатар барлық уақытта осы кіші жүйенің энергиясы болатын микрокүйлер болуы мүмкін. Толық жүйе микроканондық ансамблге жататындықтан, оның барлық күйлері тең ықтималдықты. Толық жүйенің күйлер санын деп белгілейік. Сонда әрбір күйдің ықтималдығы болады. Кіші жүйенің осы күйі толық жүйенің көптеген күйлері арқылы орындалады. Сондай күйлер санын деп белгілесек, онда кіші жүйенің энергиясы күйде болуының ықтималдығы микроканондық ансамбльдегі ықтималдық анықтамасына сәйкес былай анықталады:

(15.1)

мұндағы 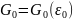– жүйе микрокүйлерінің толық саны, ал 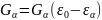– кіші жүйенің энергиясы болатын күйді іске асыратын жүйенің микрокүйлерінің толық саны.

(15.1) формуланы практикада қолдану үшін, 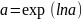қатынасын қолданыпмынадай түрде жазуға болады:

(15.2)

энергиясы энергиясымен салыстырғанда өте аз мәнге ие, ал логарифм үлкен мәнді аргументтерге тәуелді өте баяу өзгеретін функция. Сондықтан -ны нүктесінде бойынша сызықтық мүшеге дейін Тейлор қатарына жаюға болады:

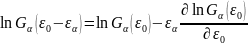(15.3)

Мұндағы - қарастырылатын кіші жүйенің нөлдік энергияға сәйкес күйін іске асыратын толық жүйенің микрокүйлерінің саны және бұл сан -ға тәуелді емес, демек . Сондай-ақ энергияның өсуімен микрокүйлер саны артады, демек , сондықтан

(15.4)

-дан тәуелсіз оң мәнді тұрақты шама. Кіші жүйе жүйенің кез келген кішігірім бөлігі болуы мүмкін, сондықтан кіші жүйе үшін және жүйе үшін де тұрақтысы бірдей мәнге ие. Демек тұрақтысы канондық және микроканондық ансамблдерді сипаттайтын іргелі шама болып табылады. Бұл іргелі шама температура болып табылады, ал температурамен қарапайым формуламен байланысқан:

(15.5)

(15.3) және (15.4) өрнектерін ескерсек, онда (15.2) формуласын мына түрде жаза аламыз:

(15.6)

мұндағы –тұрақты.

(15.6) формула Гиббс таралуы немесе канондық таралу деп аталады. -кіші жүйенің энергиясы болатын бір күйінің ықтималдығы.

Бақылау сұрақтары:

1. Ықтималдықтар теориясында оқиға дегеніміз не?

2. Сынақ дегеніміз не?

3. Қандай оқиғаны айқын оқиға деп атаймыз?

4. Қандай оқиғаны кездейсоқ оқиға деп атаймыз? Мысалдар келтіріңіз.

5. Қандай оқиғалар сәйкес емес оқиғалар деп аталады?