§14. Макрокүйдің ықтималдығы

1. Макрокүйдің ықтималдығы. Макрокүй көптеген микрокүйлер арқылы жүзеге асады. Егер қарастырылатын макрокүйді сипаттайтын қасиеттер белгілі болса, онда осы қасиеттерді қанағаттандыратын барлық микрокүйлерді санап шығуға болады. Микрокүйлер санын деп белгілейік, мұндағы 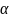-макрокүйді сипаттайды, ал жүйенің барлық мүмкін күйлер санын деп белгілейік. Микрокүйлердің тең ықтималдылық постулатына және ықтималдық анықтамасына сәйкес қарастырылатын макрокүйдің ықтималдығы былай анықталады:

(14.1)

Микрокүйлер саны макрокүйдің термодинамикалық ықтималдылығы деп аталады. Бұл сан математикалық түсініктегі ықтималдылық емес, саны өте үлкен мәндерге ие. Солай бола тұра бұл сан термодинамикалық ықтималдылық деп аталады, себебі (14.1) формуласымен сәйкес макрокүйдің ықтималдығы анықталады. (14.1) формуласындағы күйлер санын анықтау теориялық мәселе болып табылады. Әрине, күйлер санын тікелей анықтау барлық уақытта мүмкін бола бермейді. Сондықтан көптеген жағдайларда күйлер санын оларды санамай-ақ анықтау немесе күйлер санын білмей-ақ ықтималдығын анықтау негізгі теориялық мәселе болып табылады. Егер газ идеал болса, онда кеңістіктік айнымалылар бойынша микрокүйлердің санын тікелей санауға болады. Бөлшектердің координаталар (кеңістіктік ұяшықтар) және импульстері (импульстік ұяшықтар) бойынша таралуларын бір біріне тәуелсіз деп қарастыруға болады. Сондықтан жүйенің микрокүйлерінің толық санын кеңістіктік микрокүйлер мен импульстік микрокүйлер сандарының көбейтіндісіне тең деп алуға болады.

Қандай да бір макроскопиялық кеңістіктік таралудың ықтималдығын анықтағанда және микрокүйлер санын есептегенде импульстік күйлер саны бірдей болады. Сондықтан импульстік күйлер саны (14.1) формуланың алымына және бөліміне көбейтіледі де қысқарып кетеді. Жүйенің кеңістіктік макрокүйінің ықтималдығын есептегенде және сандарын кеңістіктік микрокүйлердің сандары ретінде алуға болады.

2. Макрокүйдің ықтималдығын есептеу. Идеал газ алып тұрған көлемді , осы көлемдегі бөлшектер санын деп белгілейік. Бөлшектер орналасуы мүмкін ұяшықтар саны , мұндағы 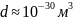. Ұяшықтар саны өте көп және шарты үнемі орындалады. көлемнің бір бөлігі болатын қандай да бір нақты көлемде бөлшектердің саны болатын жүйенің макроскопиялық күйінің ықтималдығын анықтайық (10-сурет). Есептің шарты бойынша және . Сондай-ақ көлемі аз болмауы керек, оның ішінде кем дегенде бөлшектер саны орналасатындай ұяшықтар болуы керек. көлемдегі ұяшықтар саны 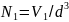, сондықтан 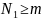болады. Жүйенің толық микрокүйлерінің саны бөлшектерді ұяшықтарға орналастыру әдістерінің санына тең. Сонымен, жүйедегі микрокүйлердің толық саны былай анықталады:

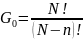(14.2)

Енді көлемде бөлшектер санының орналасуы макрокүйіне сәйкес микрокүйлердің санын анықтайық. Мұндай микрокүйлер санын g -деп белгілейік. Сонымен,

(14.3)

Көлемнің қалған бөлігінде басқа бөлшектер бар. Осы қалған бөлшектер үшін мүмкін болатын микрокүйлер саны былай анықталады:

(14.4)

Сонымен, көлемдегі бөлшектер үшін қарастырылып отырған макрокүй орындалатын микрокүйлер саны көбейтіндісіне тең болады. Алайда бұл көбейтінді макрокүй орындалатын барлық микрокүйлер санын бермейді. Бұл тек бөлшектердің көлемдегі нақты жиынтығына сәйкес келетін микрокүйлер санын береді. бөлшектерді барлық бөлшектерден әдіспен таңдап алуға болады. Сондықтан макрокүй орындалатын микрокүйлердің толық саны былай анықталады:

(14.5)

(14.1)және (14.5) формулалардың негізінде макрокүйдің ықтималдығын былай анықтауға болады:

(14.6)

Сонымен макрокүйдің ықтималдығын анықтайтын формуланы шығардық. Бірақ, бұл формуланың құрамына енетін сандар өте үлкен. Егер газ қалыпты жағдайда тұр десек, онда болғанда , болар еді. Сондықтан көлемі көлемнің азырақ бөлігі болса да ондағы ұяшықтар саны өте көп, демек деп ескеруге болады. Бұл жағдайда (14.6) формуласы ықшамдалады.

3. Стирлинг формуласы. саны үлкен мәнге ие болғанда мына теңдік орындалады:

(14.7)

(14.7) формуласы Стирлинг формуласы деп аталады. Бұл формуланы дәлелдеу үшін мына теңдікті қарастырамыз:

санынымен салыстырғанда өте аз болғандықтан (14.8) өрнектегі сумманы интеграл түрінде жазамыз:

бұл өрнектің оң жағындағы бір саны санынан өте аз болғандықтан ескерілмеді. (14.9) өрнекті потенцирлесек (14.7) формуласын аламыз.

4. Макрокүйдің ықтималдығының формуласы. (14.6) өрнектегі барлық факториалдарды (14.7) формуладағыдай дәрежелер арқылы өрнектеу керек. Стирлинг формуласын қолданғанда , және екендігін ескеру керек. Мысалы,

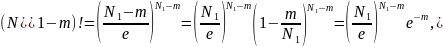
мұндағы

Осылай басқа факториалдар да есептеледі. Осының нәтижесінде (14.9) формула мынадай түрге келеді:

(14.10)

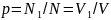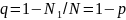Бұл формуланың мағынасы мынада: - бөлшектің көлемде болуының ықтималдығы; – бөлшектің көлемнің басқа бөлігінде болуының ықтималдығы. Осыларды ескеріп (14.10) формуланы және ықтималдықтары арқылы мына түрге келтіруге болады:

(14.11)

Бұл таралу биномдық таралу болып табылады (11-сурет). (14.11) таралуы көлемін таңдауға тәуелді емес. 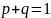болғандықтан (14.11) таралуын мына түрде жазуға болады:

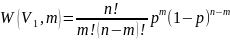(14.12)

Біз қарастырып отырған мысалды жалпы түрде қарастырайық. деп тәуелсіз оқиғаларды алайық, онда олардың ықтималдықтары болады және олар үшін нормирлену шарты орындалады. рет сынақ өткізгенде орындалатын оқиғалардың нақты тізбегі болуының ықтималдықтары болады. Осы орындалған оқиғалар тізбегінде 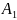оқиғасы рет, 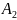– рет, ал 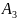– рет, т.с.с. орындалуының ықтималдығы былай анықталады:

(14.13)

(14.12)биномдық таралуы (14.13) формуланың дербес жағдайы болып табылады.

5. Биномдық таралудың шекті түрлері, Пуассон таралуы. Егер сынақтар саны шексіздікке ұмтылса ( ), онда (14.12) биномдық таралуы шексіздікке ұмтылу шартына байланысты бір шекті түрлерге айналады. Біз екі ерекше шекті жағдайларды қарастырамыз: 1) егер 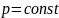жағдайында болса, онда біз қалыпты таралуды аламыз; 2) жағдайында болса, онда Пуассон таралуын аламыз.

– деп көлемдегі бөлшектердің орташа санын алайық. барлық көлемдегі бөлшектердің орташа концентрациясы болғандықтан 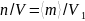немесе 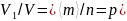болады. Осы қатынастарды (14.12) формулаға қойсақ, онда мынадай өрнек аламыз:

Осы өрнектің оң жағын ықшамдайық:

Осыдан шартын қанағаттандырсақ биномдық таралуға сәйкес келетін өрнекті аламыз:

Бұл жерде кеңінен белгілі шегі қолданылды. Осы (14.4) өрнегі Пуассон таралуы болып табылады.

Бақылау сұрақтары:

1. Ықтималдықтар теориясында оқиға дегеніміз не?

2. Сынақ дегеніміз не?

3. Қандай оқиғаны айқын оқиға деп атаймыз?

4. Қандай оқиғаны кездейсоқ оқиға деп атаймыз? Мысалдар келтіріңіз.

5. Қандай оқиғалар сәйкес емес оқиғалар деп аталады?