1.5.4. Асимптоты кривых вэз

Рассмотрим n-слойную горизонтально-слоистую среду. Мощность последнего слоя будем считать равной бесконечности. При разносах, много меньших мощности первого слоя можно пренебрегать влиянием второго слоя и считать нашу среду однородной с удельным сопротивлением _1. Таким образом, при стремлении разноса к нулю кажущееся сопротивление стремится к удельному сопротивлению первого слоя. При увеличении разноса, если он значительно превысит суммарную мощность, кажущееся сопротивление выходит на значение удельного сопротивления последнего слоя, имеющего бесконечную мощность.

А что будет с кривой ВЭЗ, если сопротивление этого слоя очень велико, то есть в основании нашего разреза лежит изолятор - _N =  ? Для ответа на этот вопрос рассмотрим поле точечного источника на поверхности тонкого проводящего слоя, лежащего на изоляторе. Ток I в этом случае будет растекаться равномерно по слою. На расстоянии r, значительно превышающих толщину слоя h, практически весь ток будет протекать равномерно через боковую поверхность цилиндра радиуса r, основания которого лежат на дневной поверхности и поверхности слоя изолятора. Площадь боковой поверхности есть . Плотность тока будет равна по модулю

,

следовательно,

^.

Кажущееся сопротивление определяется по формуле (8), где - поле в однородным полупространстве с удельным сопротивлением, равным удельному сопротивлению первого слоя:

.

Тогда

где S₁=h/ρ₁ – продольная проводимость слоя.

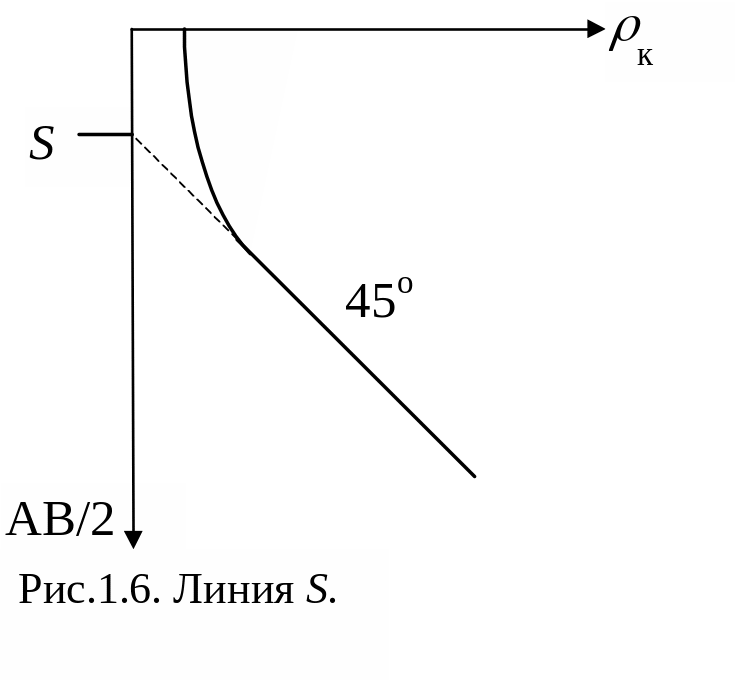В двойном логарифмическом масштабе асимптота кривой ВЭЗ пойдет в этом случае под углом 45^о к осям. Действительно,

log _k = log r - log S

Аналогично можно показать, что для N-слойной среды _к r/ S_., где S_= S₁+ S₂+…. S_n-1.

Из полученного выражения виден простой способ определения суммарной продольной проводимости разреза в случае, когда в основании его лежит изолятор. Значение этой проводимости будет численно равно значению разноса в точке пересечения продолжения асимптоты с осью ординат (см. рис.1.6).

1.5.5. Принципы эквивалентности

В некоторых ситуациях для различных разрезов мы будем получать практически одинаковые кривые кажущегося сопротивления. Рассмотрим разрез типа Н. В случае контрастного по электропроводности разреза, мы можем говорить, что хорошо проводящий слой заключен между двумя плохо проводящими. В этом случае ток между электродами А и В будет, в основном, течь по проводящему слою параллельно его границам. (Рис.1.7а).

В этом случае разность потенциалов, измеряемая на поверхности, будет одинаково зависеть и от мощности проводящего слоя, и от его удельного сопротивления. Если незначительно увеличить мощность и одновременно увеличить удельное сопротивление, суммарный эффект, создаваемый слоем не изменится. Таким образом, кривая кажущегося сопротивления будет в некоторых пределах зависеть только от продольной проводимости второго слоя S. Мы не сможем по этой кривой определить отдельно ₂ и h₂, а можем получить только отношение S₂= h₂/₂. Кривая не м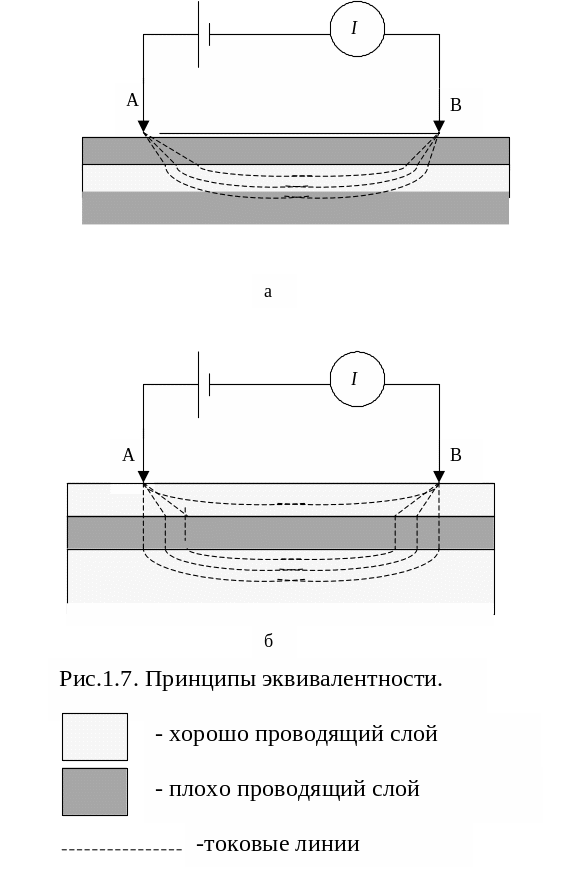 еняется,

если продольная проводи-

мость S остается постоянной.

Этот эффект называют

S- эквивалентностью. Можно пред-

ставить второй слой в виде

пачки проводящих слоев.

Этому случаю будет соответ-

ствовать модель параллельно включенных сопротивлений, в

которой общая проводимость определяется суммой проводимостей.

Совсем иную картину мы получим, если плохо проводящий слой заключен между двумя хорошо проводящими (разрез типа К). В этом случае ток будет стремиться преодолеть плохой проводник по минимальному пути, то есть токовые линии будут в первом приближении перпендикулярны границам слоя. (Рис.1.7б). В такой ситуации значение разности потенциалов на поверхности не будет существенно меняться, если мы, увеличив мощность слоя, уменьшим его сопротивление. Иными словами, кривая ВЭЗ не будет существенно меняться, если постоянной в некоторых пределах остается величина Т₂ =h₂₂, для обозначения которой часто используют термин “поперечное сопротивление”. Такой эффект называют Т-эквивалентностью. Если представить второй слой в виде пачки слоев, можно рассматривать модель последовательно включенных сопротивлений, для которой общее сопротивление равно сумме отдельных сопротивлений.

S-эквивалентность проявляется в разрезах типа Н и А, Т-эквивалентность – в разрезах типа К и Q. С формальной математической точки зрения обратная задача ВЭЗ всегда имеет единственное решение. Однако такое решение может быть получено в идеальных условиях, при отсутствии погрешностей и при бесконечно большом числе отсчетов на кривой ВЭЗ. Реально такие условия никогда не выполняются, поэтому в тех случаях, когда действуют принципы эквивалентности, интерпретация кривых ВЭЗ принципиально неоднозначна. Границы применимости принципов эквивалентности устанавливаются при математическом моделировании путем анализа взаимозависимости параметров разреза. Эти границы сужаются при сгущении сети разносов. В практике, для того чтобы получить однозначный разрез в случае, если мы имеем дело с эквивалентностью, необходимо привлекать дополнительную информацию, например данные бурения.