Правила выбора моделей временных рядов
Выбор одной из двух моделей осуществляется на основе анализа структуры сезонних колебаний.
Аддитивную модель строят в том случае, если амплитуда колебаний приблизительно постоянна.
В аддитивной модели временного ряда предполагаются значения сезонной компоненты постоянными для различных циклов.
Мультипликативную модель строят в том случае, если амплитуда сезонних колебаний возрастает или уменьшается.
В мультипликативной модели значения сезонной компоненты зависят от уровня временного ряда.
Этапы построения модели временного ряда
Рассмотрим модели временних рядов, содержащие трендовую, сезонную и случайную составляющие.
Уt = f1t + f2t + et,
Уt = f1t*f2t*et.
Построение аддитивной и мультипликативной модели сводится к расчету значений f1t, f2t, et для каждого уровня ряда.
Процесс построения модели включает в себя следующие шаги.
1. Выравнивание исходного ряда методом скользящей средней.
2. Расчет значений сезонной компоненты f2t.
3. Устранение сезонной компоненты из исходных уровней ряда и получене выравненных данных.
4. Расчет f1t, при условии устранения влияния сезонной компоненты.
5. Расчет значений временно ряда при совместном влиянии значений f1t и f2t.
6. Расчет ошибки модели.
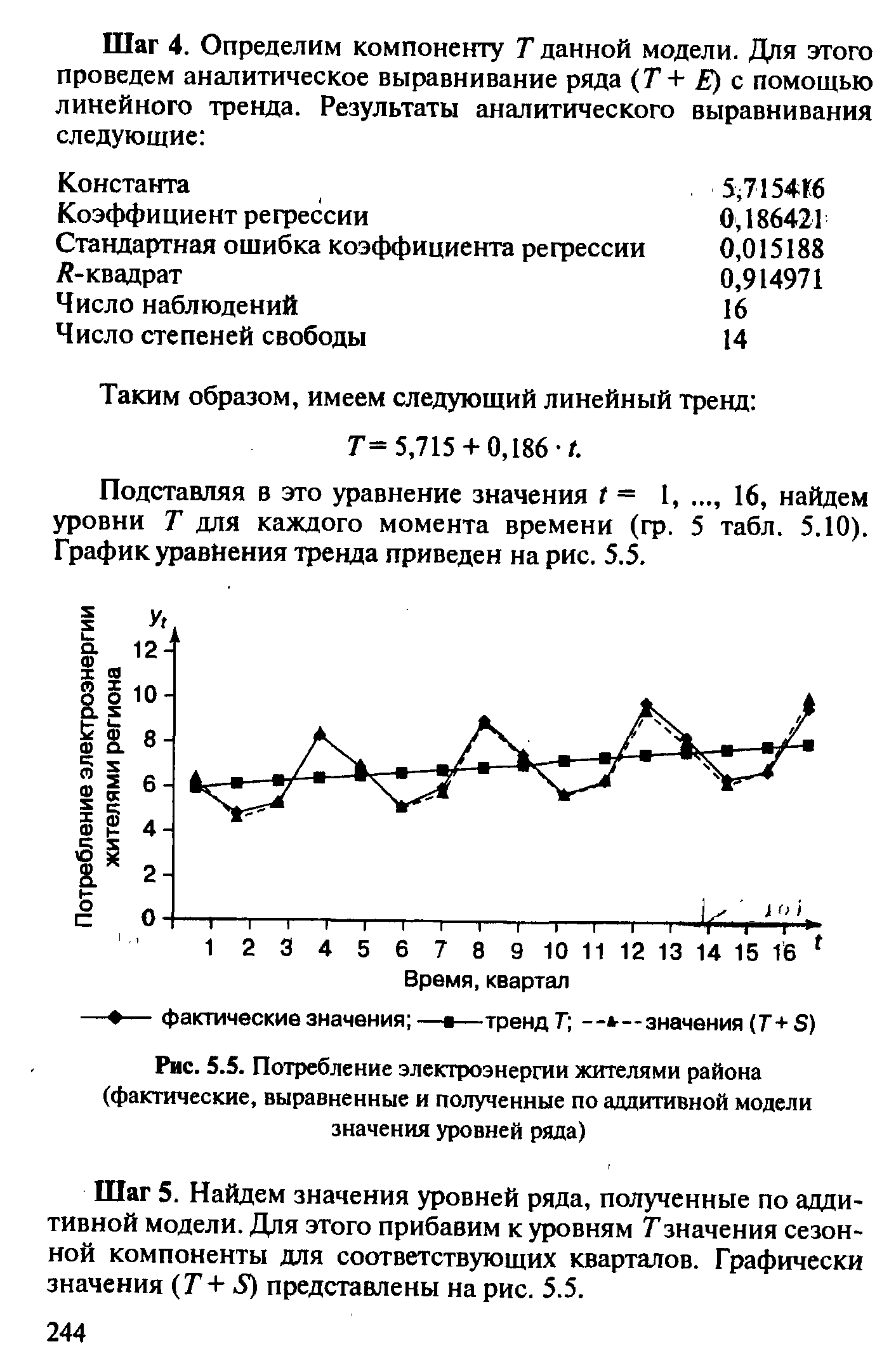
Примеры построения моделей временных рядов
Тема 20. Модели стационарных и нестационарных временных рядов и их идентификация
20.1.Определение строго стационарных временных рядов
Стационарные временные ряды – это такие ряды вероятностные свойства которых не изменяются во времени.
Временной ряд Уt (t=1, 2,…, n) называется строго стационарным, если совместное распределение вероятностей n наблюдений У1, У2,…, Уn такое же, как и n наблюдений У1+ τ, У2+ τ,…, Уn+ τ при любых n, t, τ.
Где ряды У1, У2,…, Уn и У1+τ , У2+τ,…, Уn+τ. являются сдвинутыми относительно друг друга на τ единиц или с лагом τ.
Таким образом, свойства строго стационарных рядов не зависят от момента времени t.
Временной ряд имеет три характеристики:
- среднее значение,
- дисперсия,
- автокорреляция.
Временной ряд будет стационарен, если:
среднее значение будет одинаковым на любом его отрезке,
дисперсия временного ряда будет одинаковой на любом его отрезке или гомоскедастичной (однородной, одинаковой),
автокорреляция является постоянной на любом участке временного ряда.
Временной ряд называется нестационарным, если характеристики временного ряда:
- среднее значение,
- дисперсия,
- автокорреляция
зависят от времени.
Например, временной ряд является нестционарным
- если среднее значение временного ряда линейно зависит от времени, то это означает наличие во временном ряду линейной тенденции,
- если дисперсия временного ряда изменяется во времени или является гетероскедастичной (неоднородной),
- если автокорреляционная функция циклически изменяется, то это говорит о том, что временной ряд содержит периодические составляющие.
20.2.Проверка стационарности временных рядов
Проверка стационарности временного ряда по характеристике среднее значение.
Проверим на стационарность временной ряд по характеристике: среднее значение по следующим этапам.
Этап 1. Выдвигается нулевая гипотеза о том, что среднее значение временного ряда является константой или коэффициент а1 линейной модели равен нулю:
H0: а1=0.
Этап 2. Проверка нулевой гипотезы H0: а1=0 проводится с помощью критерия Стьюдента для коэффициента а1 линейной модели Уt = а0+а1*t + et.
Расчеты характеристик модели можно выполнить с помощью функции ЛИНЕЙН.
Если нулевая гипотеза принимается, то считается, что временной ряд имеет среднее значение, не изменяющееся во времени, т.е. временной ряд не содержит возрастающей или снижающейся тенденции.
Проверка стационарности временного ряда по характеристике автокорреляции.
Стационарный временной ряд не должен содержать одну или несколько периодических составляющих.
Периодическая составляющая проверяется с помощью визуального анализа графика временного ряда и с помощью автокорреляционной функции.
Если в автокорреляционной функции наблюдается локальный минимум или максимум, то это указывает на наличие во временном ряду периодической составляющей.
Проверка стационарности временного ряда по признаку дисперсии временного ряда.
Проверку нулевой гипотезы о том, что дисперсии временного ряда одинаковы на любом отрезке (гомоскедастичны), осуществим по критерию Фишера.
Разделим временной ряд на три равных участка, на первом и третьем участке вычислим дисперсии временного ряда и сравним между собой по критерию Фишера.
Если фактическое значение критерия Фишера будет больше табличного, то нулевая гипотеза отвергается и утверждается, что дисперсии временного ряда являются гетероскедастичными.