Тема 10. Оценка качества подбора уравнения

10.1. Перечень показателей качества модели

Качество подбора уравнения определяется с помощью следующих трех основных показателей качества модели:

Е - ошибка модели,

Е% - ошибка модели, вычисленная в процентах,

R² – коэффициент детерминации

Ошибка модели в абсолютных значениях вычисляется по формуле:

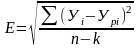
где Е – ошибка модели, выраженная в единицах измерения У,

n - объем выборки,

k - количество коэффициентов модели,

k = 2 для модели У_р = а₀+а₁*Х.

10.2. Ошибка модели, выраженная в процентах, вычисляется по формуле:

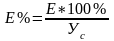
где Е% - ошибка модели, выраженная в процентах от среднего значения У.

Принято считать, что если ошибка модели будет меньше 5%, то модель является достоверной.

Для расчета R² нам потребуется произвести дисперсионный анализ регрессионной модели.

10.3. Дисперсионный анализ регрессионной модели

Дисперсия - свойство переменной Х, которая вычисляется делением вариации на ее число степеней свободы по формуле:

где n - 1 - число степеней свободы вариации,

n - объем выборки,

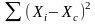- вариация признака Х.

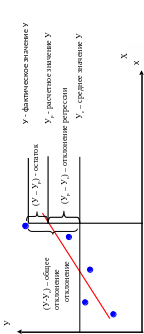Дисперсионный анализ регрессионной модели состоит в разложение вариации зависимой переменной на вариации уравнения регрессии и остатков, см. рис

10.4. Коэффициент детерминации

Коэффициент детерминации равен доли объясненной вариации от общего варьирования зависимой переменной:

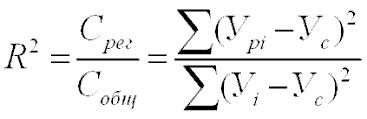
Множественный коэффициент корреляции.

Множественный коэффициент корреляции показывает степень зависимости У от факторов, включенных в модель.

Тема 11. Проверка статистической значимости эконометрической модели

11.1. Критерии проверки значимости модели.

Для проверки значимости модели используются:

- коэффициент детерминации R²

^{- и критерий Фишера F.}

11.2. Коэффициент детерминации

Коэффициент детерминации вычисляется по формуле:

Принято считать, что если коэффициент детерминации больше 0,7, то модель является хорошей.

11.3. Критерий Фишера

Для более точного утверждения используется критерий Фишера.

Фактическое значение критерия Фишера вычисляется по формуле

11.4. Проверка статистической значимости эконометрической модели

Проверка достоверности модели производится с помощью статистического критерия Фишера по следующим шагам.

Шаг 1. Выдвигается нулевая гипотеза

Н₀: " У_рi = У_с, - расчетные значения У_рi равны среднему значению У_с , т.е. при изменении Х_i У_рi не изменяются и равны среднему значению У_с или между У_i и Х_i нет связи"

Шаг 2. Вычисляется фактическое значение критерия Фишера

 

Шаг 3. Определяется критическое значение критерия Фишера на уровне значимости =0,05.

_Fкр(α = 0,05, M₁ = k - 1, М₂ = n - k),

где - уровень значимости

М₁ - число степеней свободы для большей дисперсии регрессии,

М₂ - число степеней свободы для меньшей дисперсии остатков,

n – объем выборки,

k – количество коэффициентов в уравнении регрессии.

Шаг 4. Сравниваются фактические значения критерия Фишера с его критическим значением.

Если F > F_кр,(α = 0,05, М₁ = k-1, М₂ = n-k)_, то нулевая гипотеза отвергается с вероятностью 1- и считается, что модель является достоверной.

Если F < F_кр( α= 0,05, М₁ = k-1, М₂ = n-k), то нулевая гипотеза принимается и считается, что достоверность модели не доказана.