Ответы и решения к упражнениям и задачам

Элементы теории вероятностей и математической статистики

Упражнение 1.

Ответ: а) да; б) нет; в) да; г) нет.

Упражнение 2.

Ответ: а) да; б) нет; в) да; г) нет; д) нет.

Упражнение 3.

Ответ: а) да; б) нет; в) в общем случае нет; г) нет; д) да; е) да.

Задача 1.

Решение.

1) Событие А – выпадение одного очка, число благоприятных исходов m = 1.

Число возможных исходов n = 6: всего шесть граней, может выпасть 1, 2, 3, 4, 5 или 6.

Р(А) = m/n = 1/6

2) Событие В – выпадение нечётного числа очков – это 1, 3 или 5, число благоприятных исходов m = 3.

Всего исходов, как показано выше, n = 6.

Р(В) = m/n = 3/6 = 1/2

3) Событие С – выпадение не менее трёх очков – это 6, 5, 4 или 3, число благоприятных исходов m = 4.

Всего исходов n = 6.

Р(С) = m/n = 4/6 = 2/3 

Задача 2.

Решение.

1. Равновероятными элементарными исходами опыта являются следующие:

w₁ – орёл выпал на обеих монетах,

w₂ – орёл выпал только на медной монете,

w₃ – орёл выпал только на серебряной монете,

w₄ – орёл не выпал ни на одной монете,

т.е. n=4.

2. Благоприятным является только один исход w₁, т.е. m=1.

3. Получаем: P .

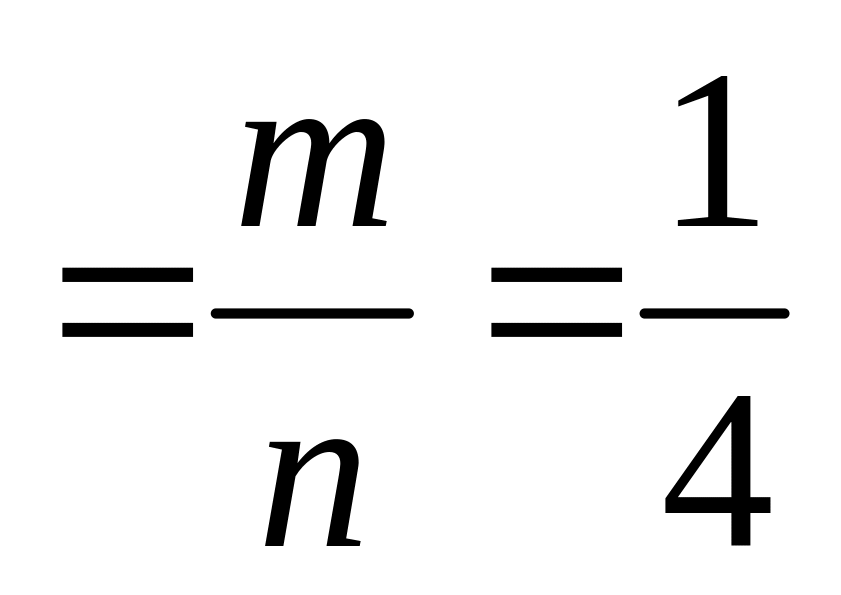Задача 3.

Решение.

1. Равновозможными элементарными исходами здесь являются пары (x, y), где x и y принимают значения 1, 2, 3, 4, 5 или 6.

2. Общее число элементарных исходов n = 6  6 = 36, т.к. x может меняться от 1 до 6 и y может меняться от 1 до 6 независимо друг от друга (см. применение правила произведения в разделе «Структуры на множестве. Элементы комбинаторики»).

3. 7 – это пары (1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1), m₁=6.

8 – это пары (2, 6), (3, 5), (4, 4), (5, 3), (6, 2), m₂=5.

4. P₁ ,

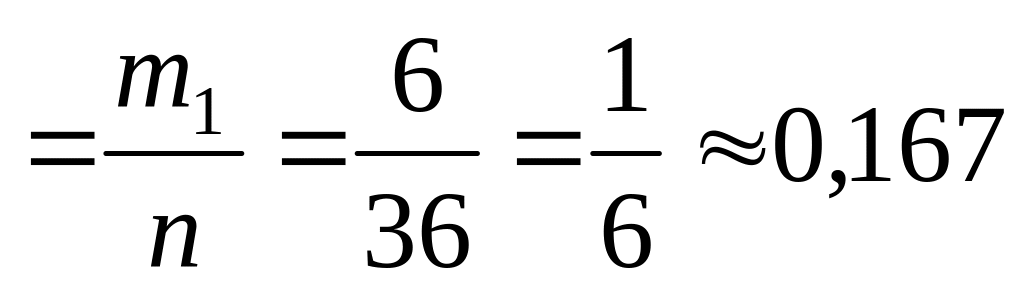P₂ ,

P₁  P₂ , таким образом , «сумма очков 7» есть более вероятное событие, чем «сумма очков 8».

5. Интересно отметить, что этот факт («сумма очков 7» есть более вероятное событие, чем «сумма очков 8») был замечен игроками в кости. Попытки его объяснить (и решение ряда задач по страхованию и т.п.) привели к созданию математической теории – начал теории вероятностей.

Задача 4.

Ответы (см. решение задачи 5 раздела «Случайные события и их вероятности»):

а) Р = 3/12 = 1/4; б) Р = 4/12 = 1/3; в) Р = 0; г) Р = 5/12.

Задача 5.

Решение.

Ход рассуждений см. в решении задачи 5 раздела «Случайные события и их вероятности».

1. Р = m/n = 0,99

2. m = 2 + x, где х – искомое число белых шаров, которые надо добавить в урну;

n = 2 + 8 = 10.

3. Получаем: 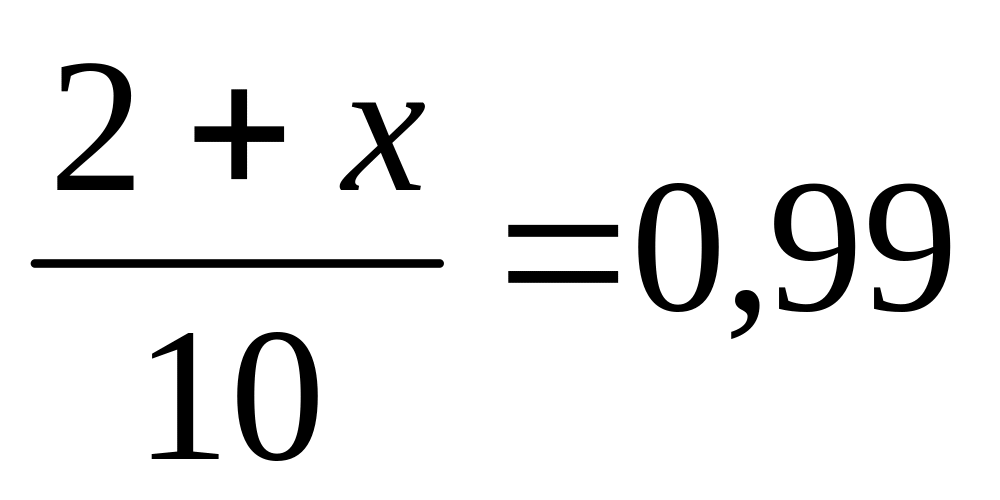; 2 + х = 9,9; х = 9,9 – 2 = 7,9. Это означает, что надо добавить 8 белых шаров.

Задача 6.

Решение.

1) Число возможных исходов – два вопроса из общего количества вопросов – это число сочетаний из 40 по 2, т.е. n = С₄₀² .

2) Число благоприятных исходов – два вопроса из подготовленных – это число сочетаний из 30 по 2, т.е. m = С₃₀^{2 .}

3) .

Задача 7.

Решение.

1) Число благоприятных исходов m=1.

2) Число возможных исходов – это число размещений из 10 по 4 (см. раздел, посвящённый комбинаторике), т.к. в числе цифрового кода четыре позиции хххх, в каждой из которых х может меняться от 0 до 9 включительно, причём совпадений быть не должно, т.к. по условию задачи все цифры в коде различны, т.е. n = A₁₀⁴ .

3) .

Задача 8.

Решение.

1) х х х  шаблон трёхзначного числа

91010 = 900 = n – число вариантов всех возможных трёхзначных чисел, т.к в крайнем левом разряде могут быть цифры от 1 до 9 включительно, в предыдущем от него разряде – цифры от 0 до 9 включительно, в крайнем правом – цифры от 0 до 9 включительно (см. «Ответы и решения к упражнениям и задачам», раздел «Структуры на множестве. Элементы комбинаторики», решение задачи 2).

2) Нас интересует событие А = «у выбранного числа совпадают хотя бы две цифры». Однако проще вычислить вероятность события А = «у выбранного числа все цифры различны».

3) Если все цифры в трёхзначном числе различны:

y y y

9  9  8 = 648 = m₁ – число возможных вариантов (см. «Ответы и решения к упражнениям и задачам», раздел «Структуры на множестве. Элементы комбинаторики», решение задачи 4).

4) ; P(A) = 1 – P(A) = 1 – 0,72 = 0,28.

Задача 9.

Решение.

а)