10. Основные числовые характеристики непрерывных случайных величин
1
.
Математическим
ожиданием
непрерывной случайной величины X
с плотностью распределения j(х)
называется число а
= М(Х), определяемое равенством:
Дисперсией D(X) непрерывной случайной величины называется математическое ожидание квадрата отклонения случайной величины от её математического ожидания:
D(Х) = М[Х-a]2, а=M(X).
11.Равновероятностный закон распределения вероятностей.
Функция распределения случайной величины Х, распределенной по равномерному закону, есть
F(x)
Её математическое ожидание:
И дисперсия:
Равномерный закон распределения
Непрерывная случайная величина X имеет равномерный законраспределения на отрезке [a, b], если её плотность вероятности постоянна на этом отрезке и равна нулю вне его, т.e.
12. Биномиальный закон распределения вероятностей.
Дискретная случайная величина X имеет биномиальный закон распределения, если она принимает значения 0,1, 2,…,m,….,n с вероятностями р(m) = Р(Х = m) = Cnm рm qn-m, где 0 < p <1,
q = 1─ р.
Биномиальный закон распределения представляет собой закон распределения числа Х = m наступлений события А в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью р.
Теорема. Математическое ожидание и дисперсия случайной величины, распределенной по биномиальному закону, даются формулами
M(X) = np, D(X) = npq.
Следствие. Математическое ожидание величины (m/n) в n независимых испытаниях, в каждом из которых оно может наступить с одной и той же вероятностью р, равно р, т.е. M(m/n) = р, D(m /n)=pq/n.
13.Закон распределения вероятностей Пуассона.
Дискретная случайная величина X имеет закон распределения Пуассона, если она принимает значения 0,1 2,…,m,…,n с вероятностями р(m) = Р(Х=m) =е─λ λm/m! , где λ = np.
Tеорема. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру λ этого закона. М(Х) = λ, D(X)= λ.
Распределение Пуассона ─ частный случай биномиального закона распределения для относительно больших n и относительно малых р.
14.Нормальный закон распределения вероятностей.
Н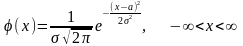
епрерывная
случайная величина X
имеет нормальный
закон распределения (закон
Гаусса) с
параметрами а
и s2
, если её плотность вероятности имеет
вид:
Кривую нормального закона распределения, называют гауссовой кривой.
Теорема 1. Математическое ожидание случайной величины X, распределённой по нормальному закону, равно параметру а этого закона, а дисперсия - параметру s2, т. е. М(Х) = a, D(X)= s2.
Ф
ункция
распределении случайной величины X,
распределённой по нормальному закону
имеет вид:
В частном случае, когда а=0, а s2=1 нормальное распределение называется стандартным.
Т
еорема
2. Функция
распределении случайной величины X,
распределённой по стандартному
нормальному закону, выражается через
функцию Лапласа Ф0(х)
по формуле
где:
В общем случае
Свойства нормального распределения
1
.
Вероятность попадания случайной
величины X,
распределённой по нормальному закону,
в интервал [х1,
х2],
равна
2. Вероятность того, что отклонение случайной величины X, распределенной по нормальному закону, от математического ожидания a не превысит величину D> 0 , равно:
Р(½Х -а½£D) = 2Ф0 (t), t = D/s.
По этой формуле можно рассчитать вероятности Р(½Х -а½£D), для различных значений D:
D = s, Р(½Х -а½£D) = 2Ф(1)=0,6827;
D = 2s, Р(½Х -а½£D) = 2Ф(2)=0,9545;
D = 3s, Р(½Х -а½£D) = 2Ф(3)=0,9973.