- •Глава 1. Основы информационных технологий
- •1. Информация, ее виды. Свойства информации. Способы передачи информации. Кодирование информации, представление информации в компьютере. Файл. Измерение объемов информации.
- •Компьютерная графика и мультимедиа
- •5. Техн. Обработки графич. Инф-и. Виды компьютерной графики, средства ее создания. Растровая графика. Достоинства и недостатки растровой графики. Фотошоп.
- •3. Группа инструментов «Ретуширование» (Retouching tools)
- •5. Группа инструментов «Рисование» и «Текст» (Drawing and type tools)
- •Изменение формы кривой. С помощью инструмента Форма можно менять положение узлов и форму кривых путем перетаскивания узлов, их направляющих точек и линий.
- •Технологии программирования и методы алгоритмизации
- •8. Алгоритм и его св-ва. Сп-бы опис. Алг-мов. Базовые структуры алгоритмов. Основные этапы полного построения алг-мов. Структурный подход при конструировании алг-мов.
- •1. Полная форма, if–then–else:
- •If условие
- •2). Неполная форма, if–then:
- •2. Структура «Построение с известным числом повторений»
- •Структура «Повторение с постусловием»
- •10. Процедуры и функции пользователя: формальные и фактические параметры, глобальные и локальные переменные, входные и выходные данные.
- •11. Типы данных: структурный (массив) и комбинированный (запись). Алг-мы сортировки и поиска в массивах. Массивы из записей. Оператор With.
- •Var имя_записи: имя_типа;
- •Ves: real;
- •12. Понятие физ. И логич. Файла данных. Классификация файлов данных. Про-ры и ф-и работы с файлами (созд., дополн. Новыми данными, использ. Данных из файла).
- •15. Перегрузка методов и конструкторов как механизм реализации полиморфизма. Перегрузка операторов. Перегрузка бинарных, унарных оп-й и операторов отношений.
- •16. Наслед. В c#: наслед., базовые и производн. Классы. Доступы к членам базовых классов. Конструкторы и наслед-е. Вирт. Методы и их переопределение. Абстр. Классы.
- •Информационные системы и сети
- •18. Технологии обработки и хранения сложно структурированных данных. Базы данных, системы управления базами данных (субд). Модели данных. Субд ms Access:
- •19. Структурированный язык запросов: назначение, возможности и достоинства. Типовые задачи, решаемые средствами sql. Структура команды sql. Выборка данных.
- •Insert into student (student_id, city, surname, name)
- •If условие Then выражение.
- •24. Протокол http и способы передачи данных на сервер. Использование html-форм для передачи данных на сервер. Методы get и post. Обработка запросов с помощью php. Примеры разработки запросов.
- •Архитектура и программное обеспечение вычислительных систем
- •26. Память. Основная память: бит, адреса памяти, упорядочение байта, код исправления ошибок (код Хэмминга), кэш-память; модели, типы памяти. Вспомогательная память.
- •27. Базовые структуры в ассемблере. Программы с ветвлениями. Циклические программы: условие перехода Jnnn (больше, меньше, равно); безусловные переходы Jmp; команда Loop.
- •История информатики
- •Глава 2. Прикладная математика Дискретная математика
- •Способы задания графов
- •2 Рисунка графа
- •3. Эйлеровы циклы и цепи. Эйлеровы графы. Критерий эйлеровости графа. Реш. Зад. О кенигсбергских мостах. Гамильтоновы циклы и цепи. Гамильтоновы графы. Достаточные условия гамильтоновости графа.
- •Теория вероятностей и математическая статистика
- •Основные свойства плотности распределения. , т.К. – неубывающая функция; ; ; Вероятность того, что св попадет в интервал от α до β ;
- •5. Основные законы распределения случайных величин: биномиальный закон, закон Пуассона, показательный закон, нормальный закон. Функция Лапласа.
- •6. Виды измерений в статистике: количественные, порядковые, номинальные. Дискретные и интервальные вариационные ряды. Кумулятивные ряды.
- •Вычислительные методы и компьютерное моделирование
- •7. Числ. Методы решения алгебраич-х и трансцендентных уравнений с одной переменной (метод деления отрезка пополам, метод простой итерации, метод Ньютона
- •8. Приближенное вычисление значения определенного интеграла (метод трапеций, метод Симпсона, метод Монте-Карло).
- •Глава 3. Мпи
- •Шк. Курс инф-ки: цели, стр-ра. Анализ содерж. Линий курса информатики.
- •Метод. Особен. Шк. Курса инф-ки. Специфика орг-ции ур. Инф-ки, типы и стр-ра.
- •Шк. Кабинет инф-ки и информ. Технологий. Требования к технич. И методич. Оснащению кабинета. Док-ция. Беседа с уч-ся по охране труда.
- •Контроль уч. Достижений уч-ся по инф-ке. Виды и ф-мы орг. Контроля. Оценивание зн. И ум. Уч-ся по инф-ке: хар-ка 10бал. С-мы, критерии, особ-ти оцен-я в соотв. С видами к.
- •11. Методика обучения учащихся работе с базами данных: тема учебной программы, формирование основных понятий и умений, примеры заданий для учащихся.
- •15. Обуч-е уч-ся сост-ю алгоритмов с управляющей структурой «ветвление»: тема учеб. Прог-мы, формиров-е основных понятий, примеры заданий для учащихся.
- •Var a:integer;
- •Var имя_массива : array[индекс1..ИндексN] of тип_элементов;
- •Var t, f, p, s : char;
- •Var t, f, p, s : string;
- •19. Факульт-е занятия по инф-ке. Цели, анализ сод-я программ факульт-х курсов.
- •Современные информационные технологии в образовании
- •20. Совр-е усл-я внедрения инф-ых технологий (ит) в образование. Классификация ит. Информатизация с-мы образования. Актуальные направления раз-я инф-и образования.
- •21. Электр-е ср-ва обуч-я (эсо), применяемые в учебном процессе. Сценарий эсо, процесс его разработки. Классификация, цели, специфика применения различных видов эсо.
- •26. Электр учебник: требования к нему, особенности оформления и использования, средства создания. Разработка электр. Учебных материалов и их публикация в www,
- •27. Компьютерный контроль знаний: виды программ, требования к ним и особенности применения. Тестирование, как вид компьютерного контроля.
- •28. Визуализация обуч-я, виды наглядности, ср-ва созд-я объектов комп-ной графики, графич-е форматы, требования к созданию и оформлению компьютерной наглядности.
Вычислительные методы и компьютерное моделирование
7. Числ. Методы решения алгебраич-х и трансцендентных уравнений с одной переменной (метод деления отрезка пополам, метод простой итерации, метод Ньютона
Пусть
дано ур
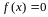 (1),
где ф-ция f(x)
определена и непрерывна в некотором
конечном или бесконечном интервале
a<x<b.
Всякое значение
(1),
где ф-ция f(x)
определена и непрерывна в некотором
конечном или бесконечном интервале
a<x<b.
Всякое значение
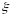 ,
обращающее ф f(x) в нуль, т.е. такое, что
,
обращающее ф f(x) в нуль, т.е. такое, что
 ,
называется корнем ур-я f(x)
= 0. Метод
деления отрезка пополам заключается
в следующем: В качестве нулевого
приближения к корню берем середину
отрезка
,
называется корнем ур-я f(x)
= 0. Метод
деления отрезка пополам заключается
в следующем: В качестве нулевого
приближения к корню берем середину
отрезка
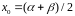 (имеется в виду, что корень уже отделен
и принадлежит отрезку
(имеется в виду, что корень уже отделен
и принадлежит отрезку
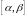 ).
Вычисляем значения функции
).
Вычисляем значения функции
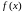 в точке
в точке
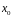 .
Из двух полученных отрезков выбираем
тот, на концах которого функция имеет
разные знаки. В качестве первого
приближения к корню принимаем середину
нового полученного отрезка и т.д. В
результате на определенном шаге получаем
либо точный корень уравнения
.
Из двух полученных отрезков выбираем
тот, на концах которого функция имеет
разные знаки. В качестве первого
приближения к корню принимаем середину
нового полученного отрезка и т.д. В
результате на определенном шаге получаем
либо точный корень уравнения
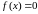 ,
либо бесконечную последовательность
вложенных друг в друга отрезков
,
либо бесконечную последовательность
вложенных друг в друга отрезков
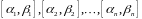 ,
таких что
,
таких что
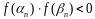 (*),
(*),
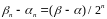 .
(**)
.
(**)
Процесс
деления отрезков пополам продолжается
до тех пор, пока длина отрезка не станет
меньше некоторого сколь угодно малого
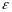 .
Любая точка последнего отрезка дает
значение корня с требуемой точностью.
Метод
простой итерации заключается
в следующем:
.
Любая точка последнего отрезка дает
значение корня с требуемой точностью.
Метод
простой итерации заключается
в следующем:
Пусть
дано уравнение (1). Заменим уравнение
(1) эквивалентным уравнением x=φ(x)
(2).
Выберем каким-либо способом грубое
приближение x0
к корню и подставим его в правую часть
уравнения (2). Тогда получим некоторое
значение x1=φ(x0)
(3).
Подставим в правую часть (3) вместо x0
значение x1
и получим новое приближение x2=φ(x1).
Повторяя
этот процесс, получаем последовательность
{xn}
приближений,
где xn=φ(xn-1),
n=1,2,…
(4).
Если полученная последовательность
{xn}
сходится,
т.е. существует
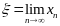 ,
то он является корнем уравнения (1).
Последовательность сходится тогда,
когда ф.φ удовл. усл: |φ’(x)|<=q<1,
a<x<b.
На практике процесс итерирования
прекращают при выполнении усл.
,
то он является корнем уравнения (1).
Последовательность сходится тогда,
когда ф.φ удовл. усл: |φ’(x)|<=q<1,
a<x<b.
На практике процесс итерирования
прекращают при выполнении усл.
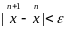 .
Получаем приближенное реш-е.
.
Получаем приближенное реш-е.
 нулевое приближение выбираем из отрезка
приближения корня.
нулевое приближение выбираем из отрезка
приближения корня.
Метод
Ньютона и секущих. Пусть
корень
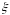 уравнения (1) отделен на отрезке
уравнения (1) отделен на отрезке
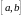 ,
причем
,
причем
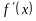 и
и
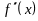 непрерывны и сохраняют определенные
знаки при
непрерывны и сохраняют определенные
знаки при
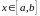 .
Найдя какое-нибудь n-ое приближенное
значение корня
.
Найдя какое-нибудь n-ое приближенное
значение корня
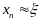 ,
,
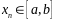 ,
мы можем уточнить его по методу Ньютона
следующим образом. Положим
,
мы можем уточнить его по методу Ньютона
следующим образом. Положим
 где
где
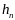 считаем малой величиной. Отсюда, применяя
формулу Тейлора, получим
считаем малой величиной. Отсюда, применяя
формулу Тейлора, получим
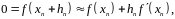 следовательно,
следовательно,
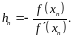 Найдем следующее приближение корня:
Найдем следующее приближение корня:
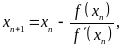
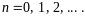
Теорема:
Если
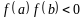 ,
причем
,
причем
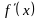 и
и
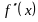 отличны от нуля и сохраняют определенные
знаки при
отличны от нуля и сохраняют определенные
знаки при
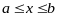 ,
то исходя из начального приближения
,
то исходя из начального приближения
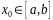 ,
удовлетворяющего неравенству
,
удовлетворяющего неравенству
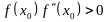 ,
можно вычислить методом Ньютона
единственный корень
уравнения (1) с любой степенью точности.
,
можно вычислить методом Ньютона
единственный корень
уравнения (1) с любой степенью точности.
Вычисления
прекращаются при выполнении
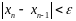 ,
где
,
где
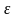 -
заданная точность.
-
заданная точность.
В
методе Ньютона на каждом шаге необходимо
вычислить три величины
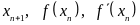 ;
при этом главная часть труда затрачивается
на нахождение
;
при этом главная часть труда затрачивается
на нахождение
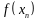 и
и
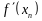 .
Кроме того, обязательным является
требование
.
Кроме того, обязательным является
требование
 .
Можно уменьшить вычислительную работу,
отказавшись от вычисления одной из
этих величин. Заметим вычисление
.
Можно уменьшить вычислительную работу,
отказавшись от вычисления одной из
этих величин. Заметим вычисление
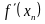 следующим образом
следующим образом
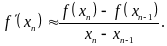
Тогда
метод Ньютона перейдет в следующую
формулу:
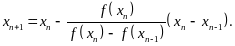 Эта формула – метод секущих.
Эта формула – метод секущих.
Геометрически
метод секущих эквивалентен замене
небольшой дуги кривой
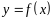 секущей, проходящей через точки
секущей, проходящей через точки
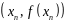 и
и
 .
.
Метод
секущих является двушаговым, т.е.
нахождение следующего значения
 требует знания двух предыдущих значений
требует знания двух предыдущих значений
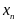 ,
,
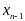 .
В частности начало расчета требует
знания двух начальных значений х0
и х1.
.
В частности начало расчета требует
знания двух начальных значений х0
и х1.