3.4.1.Проверка на случайность ряда остатков

Для проверки случайности остаточной компоненты ε можно использовать критерий поворотных точек (пиков).

Опр. Точки считаются поворотными, если:

или .

Пусть число поворотных точек равно р, тогда если

²,

то гипотеза о случайности остаточной компоненты ε с доверительной вероятностью 0,95 выполняется.

3.4.2.Проверка на равенство нулю математического ожидания ряда остатков

Среднее значение ряда остатков рассчитывается по формуле:

.

Если , то модель не содержит постоянной систематической ошибки и адекватна по критерию нулевого среднего.

Если , то для проверки гипотезы о M[ε] = 0 используем t ‑ критерия Стьюдента.

Расчетное значение этого критерия задается формулой:

Если то модель гипотеза о том M[ε] = 0 не выполняется.

3.4.3.Проверка на постоянство дисперсии ряда остатков

Если D[ε] ≠ 0, то используют метод Гольдфельда-Квандта:

- необходимо ранжировать переменную x_i;

- разделить полученную совокупность на две части;

- по каждой группе построить уравнение регрессии;

- определить остаточные суммы квадратов по формулам:

и ,

где n1 – число наблюдений в первой группе;

n2 – число наблюдений во второй группе.

- если S₁> S₂ критерий ;

- если S₂> S₁ критерий .

- чем F_расч > F_табл, тем больше нарушена предпосылка о постоянстве дисперсий остаточных величин.

3.4.4.Проверка на независимость ряда остатков

Независимости уровней ряда остатков проверяем по критерию Дарбина-Уотсона.

Вычислить значение:

.

d_расч сравнивают с нижним d₁ и верхним d₂, по таблице.

Если d_расч> d₁, то гипотеза о независимости ряда остатков выполняется.

Если d₁ <d_расч< d₁, то используют первым коэффициентом автокорреляции:

.

И если r₁ по модулю меньше табличного критического уровня r_крит, то гипотеза о независимости ряда остатков выполняется.

Если d₂ < d_расч < 2, то гипотеза о независимости ряда остатков выполняется.

Если d_расч > 2, то модель остатки коррелируют отрицательно,

Необходимо принять за d^/ = 4 – d.

3.4.5.Проверка на распределение ряда остатков по нормальному закону

Используем R/S – критерий.

В нашем случае

.

Расчетное значение R/S_ε сравнивают с табличными значениями (нижней и верхней границами данного отношения), и если значение не попадает в интервал между критическими границами, то с заданным уровнем значимости гипотеза о нормальном распределении отвергается; в противном случае гипотеза принимается.

Если ВСЕ вышеперечисленные критерии дают положительный ответ, модель АДЕКВАТНА.

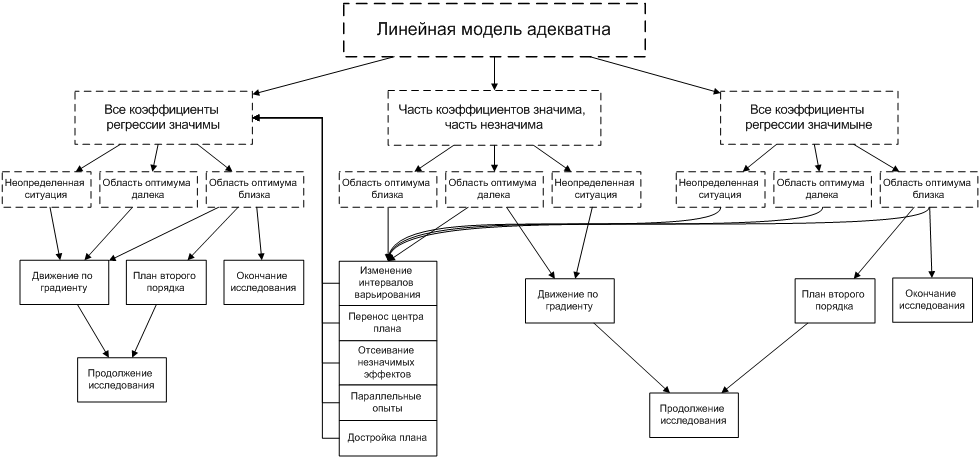
3.5.Определение меры точности модели

Точностные характеристики	Расчет и содержание характеристики
Максимальная ошибка	Соответствует Rmax =
Средняя абсолютная ошибка	, показывает на сколько в среднем отклоняется фактические значения от модуля.
Дисперсия ряда остатков	, где
Средняя квадратическая ошибка	, чем меньше ошибка, тем меньше модуль
Средняя относительная ошибка аппроксимации	. Допустимый предел значений составляет не более 8 – 15%.

3.6.Точечный и интервальный прогноз

Если модель регрессии адекватна, а параметры модели значимы, то переходят к построению прогноза.

Прогнозное значение результативного признака определяется путем подстановки в уравнение регрессии соответствующего (прогнозного) значения .

Далее вычисляется средняя стандартная ошибка прогноза:

, значит

³

и строится доверительный интервал прогноза:

.

Пример

Оценить адекватность и точность модели парной регрессии по представленным данным о спросе и доходе населения за ряд текущих лет и сделать выводы.

Год	Спрос, yi				Точки поворота
1	6	6,1	-0,10	0,01	-	-	-	0,017
2	8	7,38	0,62	0,38	1	0,72	0,52	0,078
3	8	8,66	-0,66	0,44	1	-1,28	1,64	0,083
4	10,3	9,94	0,36	0,13	1	1,02	1,04	0,035
5	10,5	11,22	-0,72	0,52	1	-1,08	1,17	0,069
6	13	12,5	0,50	0,25	-	1,22	1,49	0,038
Итого	55,8	-	0,00	1,73	4	-	5,85	0,319

Уравнение парной регрессии имеет вид: .

Проверка адекватности модели осуществляется на основе анализа остатков .

Проверка значимости модели

Значимость параметров модели оценивается с помощью t – критерия Стьюдента:

; ,

где ;

,

где .

;

, то параметр b значим;

, то параметр a не значим.

Для проверки значимости уравнения регрессии в целом используем F критерий Фишера:

.

Воспользуемся встроенными возможности электронных таблиц Excel: FРАСПОБР, которое возвращает обратное значение для F-распределения вероятностей.

Синтаксис функции:

FРАСПОБР(вероятность;степени_свободы1;степени_свободы2)

Вероятность   — это вероятность, связанная с F-распределением.

Степени_свободы1   — это числитель степеней свободы.

Степени_свободы2   — это знаменатель степеней свободы.

F_табл = FРАСПОБР(0,05;1;4) = 7,71

Поскольку: F_расч > F_табл, модель считается значимой.

Проверка выполнения предпосылок МНК

1) Проверим свойство случайности ряда остатков на основании критерия поворотных точек:

Точки считаются поворотными, если:

или .

Для выявления поворотных точек воспользуемся встроенными логическими функциями Excel: ЕСЛИ; И; ИЛИ (рисунок)

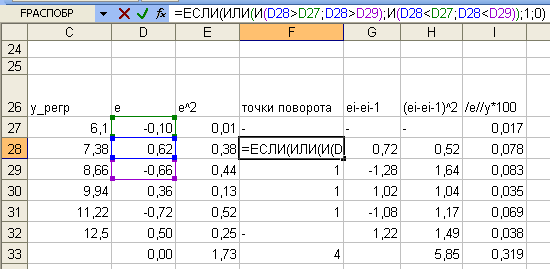
Число поворотных точек равно р = 4, тогда

⁴,

Следовательно, гипотеза о случайности остаточной компоненты ε с доверительной вероятностью 0,95 выполняется.

2) Проверим M[ε] = 0

Среднее значение ряда остатков:

, значит модель не содержит постоянной систематической ошибки и адекватна по критерию нулевого среднего.

3) Для проверка свойство на гомоскедастичности разделим совокупность на две группы.

Год	1	2	3	4	5	6
Доход, Х	10	12	14	16	18	20
Спрос, Y	6	8	8	10,3	10,5	13

Для каждой группы с помощью программы «Анализ данных» Excel инструмент «Регрессия», определяются параметры уравнений регрессии и остаточные суммы квадратов:

Группа	Уравнение регрессии	Остаток
1		= 0,666
2		= 0,882

S₂> S₁ , значит .

F_табл = FРАСПОБР(0,05;1;1) = 161,44

Поскольку: F_расч > F_табл, свойство гомоскедастичности выполняется.

4) Проверка независимость последовательности остатков ( отсутствие автокорреляции) по критерию Дарбина-Уотсона.

.

n	d1	d2
6	0,61	1,40

d_расч > 2, значит остатки коррелируют отрицательно принимаем за d^/_расч = 4 – d = 0,62.

Так как 0,61 < d^/_расч < 1,40 используют первый коэффициент автокорреляции:

.

, гипотеза о независимости ряда остатков выполняется.

5) .

Сравнивая значение R/S_ε с табличными значениями, видим, что оно попадает в интервал между критическими границами (0,1 – 0,25), значит гипотеза о нормальном распределении подтверждается.

Оценка точности модели

Средняя относительная ошибка аппроксимации:

%, а поскольку это больше 8 %, значит уровень точности можно признать приемлемым.

1 Мы определяем Var и Cov, деля соответствующие суммы квадратов на n. Это имеет свое объяснение, которое пока выходит за рамки нашего обсуждения. Вместе с тем, в разных руководствах по эконометрике Var и Cov определяются по-разному. Деление на (n – 1) используется, например, в книгах Доугерти (1997), Айвазяна и Мхитаряна (1998), тогда как в книге Магнуса, Катышева и Пересецкого (1997) соответствующие суммы квадратов делятся, на n.

2 квадратные скобки означают целую часть числа

3 t_табл - определяется по таблице распределения Стьюдента

4 квадратные скобки означают целую часть числа