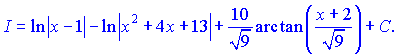16. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору

Найдем уравнение плоскости, проходящей через точку   перпендикулярно вектору 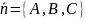, называемому нормалью к плоскости. Для любой точки плоскости 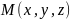 вектор  ортогонален (перпендикулярен) вектору 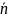, следовательно, их скалярное произведение равно нулю:

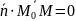 или .

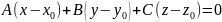35. Правила вычисления производных

Пусть функции и имеют производные в точке . Тогда

1. Константу можно выносить за знак производной.

Пример

Больше примеров решений →

2. Производная суммы/разности.

Производная суммы/разности двух функций равна сумме/разности производных от каждой из функций.

Пример

Больше примеров решений →

3. Производная произведения.

Пример

Больше примеров решений →

4. Производная частного.

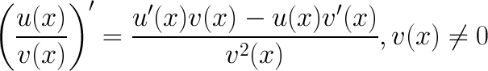
Пример

Больше примеров решений →

5. Производная сложной функции.

Производная сложной функции равна производной этой функции по промежуточному аргументу , умноженной на производную от промежуточного аргумента по основному аргументу .

и имеют производные соответственно в точках и . Тогда

Теорема

(О производной обратной функции)

Если функция непрерывна и строго монотонна в некоторой окрестности точки и дифференцируема в этой точке, то обратная функция имеет производную в точке , причем

52. Интегрирование рациональных дробей. Примеры

В предыдущей статье мы рассмотрели правила интегрирования рациональных дробей. Ниже будут приведены примеры, которые наглядно покажут как использовать эти правила и научат использовать различные приемы для получения правильного результата.

Пример 1.

Вычислить следующие интегралы

а)

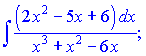
б)

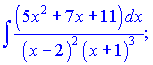
в)

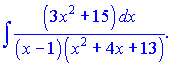
Решение.

а) Поскольку степень числителя меньше степени знаменателя, то подынтегральная функция - правильная дробь. Знаменатель

можно разложить на множители

таким образом дробь разлагается на сумму слагаемых первого типа (І):

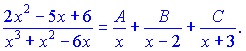
Неизвестные коэффициенты находим методом неопределенных коэффициентов. Для этого правую часть полученной только что неравенства сводим к общему знаменателю:

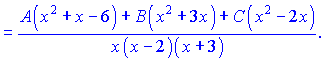
Приравниваем числители для нахождения неизвестных коэффициентов

Это равенство выполняется когда коэффициенты при одинаковых степенях  равны между собой. Из этого условия получаем систему линейных уравнений для определения неизвестных 

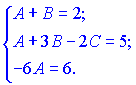
Решая ее находим неизвестные коэффициенты

Тогда подынтегральная функция примет вид

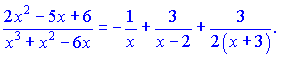
Интегрируя дроби после знака равенства получим

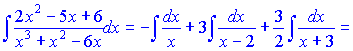
Ничего сложного в решения такого сорта примеров нет, только правильно составить и решить систему линейных уравнений для определения неизвестных.

б) Подынтегральная функция

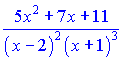
является правильной дробью, знаменатель которого имеет действительные корни. Такая дробь разлагается на сумму простейших дробей I-го и II-го типов

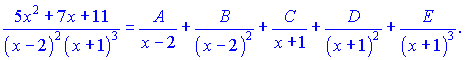
Определим неизвестные коэффициенты , для этого правую часть сведем к общему знаменателю.

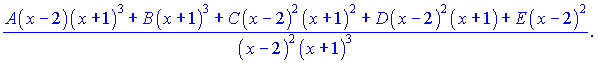
Раскрываем скобки и приравниваем коэффициенты при одинаковых степенях в числителе. Получим следующую систему линейных уравнений

Есть другой способ получения системы уравнений для определения неизвестных. Числители справа и слева должны быть равны для всех . Эта особенность несколько упрощает решение системы уравнений. Как правило, за точки  в первую очередь берут корни уравнения и значение ноль . В нашем случае это были бы значение  Ноль выбирают за счет простоты вычислений.

Решив полученную выше систему линейных уравнений, получим следующие значения неизвестных:

Интегрируем подынтегральные функции, учитывая найдены константы

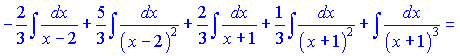
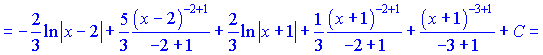
При большом количестве неизвестных в системах линейных уравнений их вычисление очень трудоемки, в то время методика приведенная выше упрощает их вычисление.

в) Подынтегральная функция

является правильной дробью. Знаменатель содержит квадратный трехчлен и множитель. Данный дробь по правилам разлагается на сумму дробей I-го и III-го типов:

Сведя к общему знаменателю, получим:

Можем приравнять коэффициенты при одинаковых степенях, но поступим иначе, чтобы научиться использовать вторую методику. Для этого подставим корень  в левую и правую часть равенства, получим

Для того, чтобы избавиться от неизвестной  подставим

Для нахождения неизвестной  выпишем неизвестные при 

Таким способом, не выписывая систем линейных уравнений и не решая их, можно достаточно быстро найти нужные константы.

Подставив найденные значения, получим интеграл

Первое слагаемое интегрируется по табличной формуле

 ко второму применяем замену переменных

и сводим к сумме двух

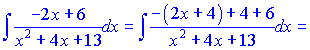
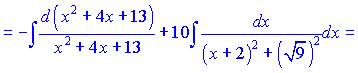
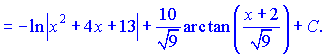
Просуммировав полученные интегралы, окончательно получим решение