
- •46. Выпуклость функции, точки перегиба
- •47. Схема полного исследования функции
- •48. Понятие дифференциала функции, его геометрический смысл. Применение к приближенным вычислениям.
- •16. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
- •35. Правила вычисления производных
- •52. Интегрирование рациональных дробей. Примеры
45. Понятие экстремума функции
Определение
Точка ![]() называется точкой
локального максимума функции
называется точкой
локального максимума функции ![]() ,
если существует такая окрестность этой
точки, что для всех
,
если существует такая окрестность этой
точки, что для всех ![]() из
этой окрестности выполняется
неравенство:
из
этой окрестности выполняется
неравенство: ![]() .
.
Точка
называется точкой
локального минимума функции
,
если существует такая окрестность этой
точки, что для всех
из
этой окрестности ![]() .
.
Значение функции в точке максимума называется локальным максимумом, значение функции в точке минимума -локальным минимумом данной функции. Локальные максимум и минимум функции называются локальными экстремумами.
Точка
называется
точкой строгого
локального максимума функции ![]() ,
если для всех
из
окрестности этой точки будет справедливо
строгое неравенство
,
если для всех
из
окрестности этой точки будет справедливо
строгое неравенство ![]() .
.
Точка
называется
точкой строгого
локального минимума функции
,
если для всех
из
окрестности этой точки будет справедливо
строгое неравенство ![]() .
.
Наибольшее или наименьшее значение функции на промежутке называется глобальным экстремумом.
Замечание
Глобальный экстремум может достигаться либо в точках локального экстремума, либо на концах отрезка.
Необходимое условие экстремума
Теорема
(Необходимое условие экстремума)
Если
функция
имеет
экстремум в точке
,
то ее производная ![]() либо
равна нулю, либо не существует.
либо
равна нулю, либо не существует.
Точки,
в которых производная равна нулю: ![]() ,
называются стационарными
точками функции.
,
называются стационарными
точками функции.
Точки,
в которых выполняется необходимое
условие экстремума для непрерывной
функции, называются критическими
точками этой
функции. То есть критические
точки -
это либо стационарные точки (решения
уравнения
),
либо это точки, в которых производная ![]() не
существует.
не
существует.
Замечание
Не в каждой своей критической точке функция обязательно имеет максимум или минимум.
Первое достаточное условие экстремума
Теорема
(Первое достаточное условие экстремума)
Пусть для функции выполнены следующие условия:
функция непрерывна в окрестности точки ;
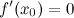 или
не
существует;
или
не
существует;производная при переходе через точку меняет свой знак.
Тогда
в точке ![]() функция
имеет
экстремум, причем это минимум, если при
переходе через точку
производная
меняет свой знак с минуса на плюс;
максимум, если при переходе через
точку
производная
меняет свой знак с плюса на минус.
функция
имеет
экстремум, причем это минимум, если при
переходе через точку
производная
меняет свой знак с минуса на плюс;
максимум, если при переходе через
точку
производная
меняет свой знак с плюса на минус.
Если производная при переходе через точку не меняет знак, то экстремума в точке нет.
Таким образом, для того чтобы исследовать функцию на экстремум, необходимо:
найти производную ;
найти критические точки, то есть такие значения , в которых или не существует;
исследовать знак производной слева и справа от каждой критической точки;
найти значение функции в экстремальных точках.
Пример
Задание. Исследовать
функцию ![]() на
экстремум.
на
экстремум.
Решение. Находим производную заданной функции:
![]()
Далее
ищем критические точки функции, для
этого решаем уравнение ![]() :
:
![]()
Первая
производная определена во всех точках.
Таким образом, имеем одну критическую
точку ![]() .
Наносим эту точку на координатную прямую
и исследуем знак производной слева и
справа от этой точки (для этого из каждого
промежутка берем произвольное значение
и находим значение производной в
выбранной точке, определяем знак
полученной величины):
.
Наносим эту точку на координатную прямую
и исследуем знак производной слева и
справа от этой точки (для этого из каждого
промежутка берем произвольное значение
и находим значение производной в
выбранной точке, определяем знак
полученной величины):

Так
как при переходе через точку
производная
сменила свой знак с "-" на "+",
то в этой точке функция достигает
минимума (или минимального значения),
причем ![]() .
.
Замечание. Также
можно определить интервалы монотонности
функции:
так как на интервале ![]() производная
производная ![]() ,
то на этом интервале функция
является
убывающей; на интервале
,
то на этом интервале функция
является
убывающей; на интервале ![]() производная
производная ![]() ,
значит заданная функция возрастает на
нем.
,
значит заданная функция возрастает на
нем.
Ответ. ![]()
Второе достаточное условие экстремума
Теорема
(Второе достаточное условие экстремума)
Пусть для функции выполнены следующие условия:
она непрерывна в окрестности точки ;
первая производная в точке ;
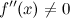 в
точке
.
в
точке
.
Тогда
в точке
достигается
экстремум, причем, если ![]() ,
то в точке
функция
имеет
минимум; если
,
то в точке
функция
имеет
минимум; если ![]() ,
то в точке
функция
достигает
максимум.
,
то в точке
функция
достигает
максимум.
Пример
Задание. Исследовать
функцию ![]() на
экстремум с помощью второй производной.
на
экстремум с помощью второй производной.
Решение. Находим первую производную заданной функции:
![]()
Находим точки, в которых первая производная равна нулю:
![]()
Вторая производная заданной функции:
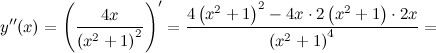
![]()
В
стационарной точке
вторая
производная ![]() ,
а значит, в этой точке функция достигает
минимум, причем
,
а значит, в этой точке функция достигает
минимум, причем ![]() .
.
Ответ.
Чтобы найти наибольшее или наименьшее значение функции на отрезке, нужно исследовать поведение функции на данном отрезке с помощью производной.
Для этого мы следуем известному алгоритму:
1. Находим ОДЗ функции.
2. Находим производную функции
3. Приравниваем производную к нулю
4. Находим промежутки, на которых производная сохраняет знак, и по ним определяем промежутки возрастания и убывания функции:
Если на
промежутке I производная функции
![]() ,
то функция
,
то функция
![]() возрастает
на этом промежутке.
возрастает
на этом промежутке.
Если на
промежутке I производная функции
![]()
![]() ,
то функция
убывает
на этом промежутке.
,
то функция
убывает
на этом промежутке.
5. Находим точки максимума и минимума функции.
В точке максимума функции производная меняет знак с «+» на «-».
В точке минимума функции производная меняет знак с «-» на «+».
6. Находим значение функции в концах отрезка,
затем сравниваем значение функции в концах отрезка и в точках максимума, и выбираем из них наибольшее, если нужно найти наибольшее значение функции
или сравниваем значение функции в концах отрезка и в точках минимума, и выбираем из них наименьшее, если нужно найти наименьшее значение функции
Однако, в зависимости от того, как себя ведет функция на отрезке, это алгоритм можно значительно сократить.
Рассмотрим
функцию ![]() .
График этой функции выглядит так:
.
График этой функции выглядит так:
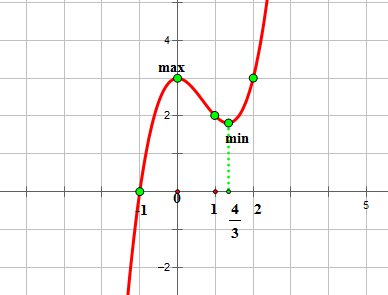 В
зависимости от того, на каком промежутке
мы будем рассматривать функцию, алгоритм
нахождения наибольшего или наименьшего
значения будет различным.
В
зависимости от того, на каком промежутке
мы будем рассматривать функцию, алгоритм
нахождения наибольшего или наименьшего
значения будет различным.
1.
Рассмотрим функцию на отрезке
![]()
Функция
возрастает на этом отрезке, поэтому
наибольшее значение она будет принимать
в правом конце отрезка:
![]() ,
а наименьшее – в левом:
,
а наименьшее – в левом:
![]() .
.
2. Рассмотрим
функцию на отрезке
![]()
Очевидно,
что наибольшее значение функция принимает
в точке максимума
,
а наименьшее – в одном из концов отрезка,
то есть надо найти значения
и
![]() и
выбрать из них наименьшее.
и
выбрать из них наименьшее.
3.
Если мы рассмотрим функцию на отрезке ![]() ,
то чтобы найти наибольшее значение, нам
нужно будет сравнить значения функции
в точке максимума и в правом конце
отрезка, то есть
и
,
то чтобы найти наибольшее значение, нам
нужно будет сравнить значения функции
в точке максимума и в правом конце
отрезка, то есть
и
![]() .
.
Чтобы найти
наименьшее значение функции, нам
нужно будет сравнить значения функции
в точке минимума и в левом конце
отрезка, то есть ![]() и
.
и
.
Эти рассуждения очевидны, если перед глазами есть график функции. Но эскиз графика легко нарисовать, проведя исследование функции с помощью производной:
1. ОДЗ функции – множество действительных чисел.
2. ![]()
3. ![]() ,
если
,
если ![]() или
или
![]()
Нанесем корни производной на числовую ось и расставим знаки. Теперь поведение функции легко определить, и, следуя за стрелками, символизирующими возрастание – убывание, можно схематично изобразить ее график:
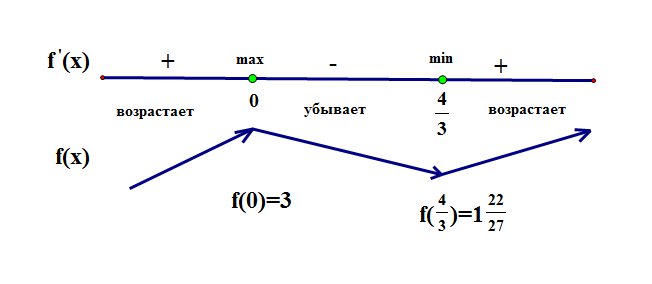
46. Выпуклость функции, точки перегиба
График
функции
,
дифференцируемой на интервале
![]() ,
является на этом интервале выпуклым,
если график этой функции в пределах
интервала
лежит
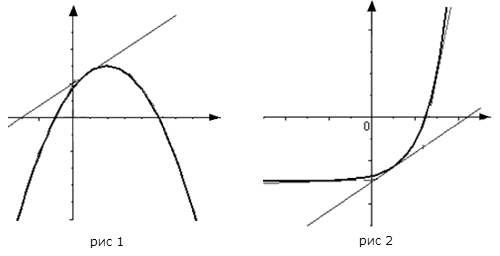
не выше любой своей касательной (рис.
1).
,
является на этом интервале выпуклым,
если график этой функции в пределах
интервала
лежит
не выше любой своей касательной (рис.
1).
График функции , дифференцируемой на интервале , является на этом интервале вогнутым, если график этой функции в пределах интервала лежит не ниже любой своей касательной (рис. 2).
Теоремы о выпуклости функции и точках перегиба
Теорема
(Об условиях выпуклости или вогнутости графика функции)
Пусть
функция
определена
на интервале
и
имеет непрерывную, не равную нулю в
точке
![]() вторую
производную. Тогда, если
вторую
производную. Тогда, если
![]() всюду
на интервале
,
то функция имеет вогнутость
на этом интервале,
если
всюду
на интервале
,
то функция имеет вогнутость
на этом интервале,
если
![]() ,
то функция имеет выпуклость.
,
то функция имеет выпуклость.
Определение
Точкой
перегиба
графика функции
называется
точка
![]() ,
разделяющая промежутки выпуклости и
вогнутости.
,
разделяющая промежутки выпуклости и
вогнутости.
Теорема
(О необходимом условии существования точки перегиба)
Если
функция
имеет
перегиб в точке
,
то
![]() или
не существует.
или
не существует.
Теорема
(О достаточном условии существования точки перегиба)
Если:
первая производная непрерывна в окрестности точки
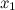 ;
;вторая производная
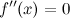 или
не существует в точке
;
или
не существует в точке
;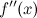 при
переходе через точку
меняет
свой знак,
при
переходе через точку
меняет
свой знак,
тогда в точке функция имеет перегиб.
Схема исследования функции на выпуклость, вогнутость
Найти вторую производную функции.
Найти точки, в которых вторая производная равна нулю или не существует.
Исследовать знак производной слева и справа от каждой найденной точки и сделать вывод об интервалах выпуклости и точках перегиба.
Пример
Задание.
Найти интервалы выпуклости/вогнутости
функции
![]()
Решение. Найдем вторую производную заданной функции:
![]()
Находим
точки, в которых вторая производная
равна нулю, для этого решаем уравнение
![]() :
:
![]()
Исследуем знак второй производной слева и справа от полученной точки:
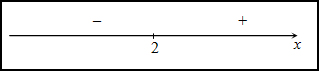
Так
как на промежутке
![]() вторая
производная
вторая
производная
![]() ,
то на этом промежутке функция
,
то на этом промежутке функция
![]() выпукла;
в силу того, что на промежутке
выпукла;
в силу того, что на промежутке
![]() вторая
производная
вторая
производная
![]() -
функция вогнута. Так как при переходе
через точку
-
функция вогнута. Так как при переходе
через точку
![]() вторая
производная сменила знак, то эта точка
является точкой перегиба графика
функции.
вторая
производная сменила знак, то эта точка
является точкой перегиба графика
функции.
Ответ. Точка - точка перегиба графика функции.
На промежутке функция выпукла, на промежутке функция вогнута.
47. Схема полного исследования функции
Ниже приведена полная схема исследования функции (или алгоритм исследования функции) по пунктам. Часть из этих шагов обычно опускается при исследовании функции, в зависимости от вида функции и требований к решению (например, для многочлена можно не проверять наличие асимптот или точек разрыва и т.п.).
Ключевые пункты (основная схема исследования) выделены черным, пункты, которые включаются в исследование опционально, выделены серым.
Найти область определения функции.
Найти область значений функции. Обычно этот пункт пропускают или заполняют после исследования на экстремумы.
Исследовать непрерывность функции, выделить особые точки (точки разрыва).
Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.
Найти точки пересечения с осями координат.
Найти нули функции. Найти интервалы знакопостоянства функции.
Установить, является ли функция чётной или нечётной. Сделать выводы о симметричности графика функции.
Установить, является ли функция периодической или нет. Обычно проверяют для тригонометрических функций, для других данный пункт пропускается.
Найти первую производную. Найти точки экстремума (локального минимума и максимума) и интервалы монотонности (возрастания и убывания) функции.
Найти вторую производную. Найти точки перегиба и интервалы выпуклости-вогнутости.
Найти наклонные/горизонтальные асимптоты функции.
Исследовать поведение функции на бесконечности.
Построить график функции. Построить асимптоты.
Отметить важные точки на графике.
Используйте этот алгоритм для решения своих заданий на исследование функций, и вы добьётесь успеха (Ох, девки, если б всё было так просто в этой жизни)))
