4 Об’єми та площі поверхонь геометричних тіл

4.1 Поняття про площу поверхні та об’єм тіла.

Площа поверхні многогранника, призми, піраміди

П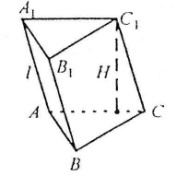 лоща повної поверхні призми дорівнює сумі площі бічної поверхні та площі двох основ:

S_повн=S_б+2S_осн

де S_осн – площа основи; S_б – площа бічної поверхні (сума площ усіх бічних граней); S_повн – площа повної поверхні.

П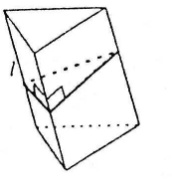 лоща бічної поверхні призми дорівнює добутку периметру перпендикулярного перерізу на довжину бічного ребра

S_б=P_перп l

де l – довжина бічного ребра, P_перп – периметр перпендикулярного перерізу.

Площа бічної поверхні прямої призми дорівнює добутку периметру основи на висоту

S_б=P_осн Н

П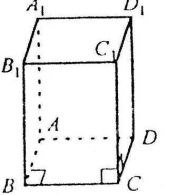 рямокутний паралелепіпед

Площа бічної поверхні дорівнює добутку периметра основи на

висоту

S_б=2(а+b)c

Площа повної поверхні дорівнює сумі площ шести прямокутників

S_повн=2(ab+ac+bc)

К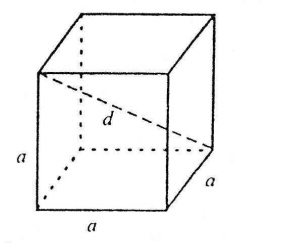 уб

Площа повної поверхні куба

S_повн=6a²

Піраміда

П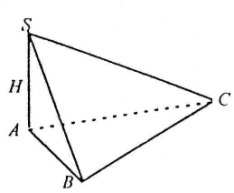 овна поверхня піраміди складається з основи та n бічних граней (відповідно до кількості вершин основи)

S_повн=S_б+ S_осн

Для правильної піраміди

П лоща бічної поверхні дорівнює половині добутку периметра основи на довжину апофеми

S_б=1/2 P_оснl

Площі основи і бічної поверхні правильної піраміди відносяться як косинус кута між бічною гранню та площиною основи:

S_осн/S_б=cos

Для зрізаної піраміди

Повна поверхня зрізаної піраміди складається з бічної поверхні та двох основ:

S_повн= S_б+S₁+S₂

де S₁ і S₂ – площі основ.

Для правильної зрізаної піраміди

Площа бічної поверхні правильної зрізаної піраміди дорівнює добутку півсуми периметрів її основ на апофему S_б=1/2(P₁+P₂) l

4.2 Об’єм призми та піраміди

Об’єм призми дорівнює добутку площі основи на висоту H

V= S_оснH

Об’єм призми дорівнює добутку площі перпендикулярного перерізу на довжину бічного ребра l

V=S_перпl

Об’єм прямокутного паралелепіпеда дорівнює добутку трьох його вимірів

V=a b c

Об’єм куба дорівнює третьому степеню (кубу) довжини його ребра

V=a³

Об’єм будь-якої піраміди дорівнює третині добутку площі основи на висоту

V= 1/3 S_осн H

4.3 Площа поверхні циліндра, конуса, кулі

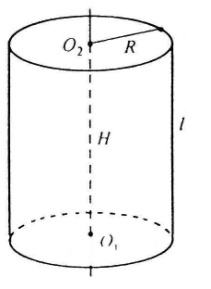
Площа бічної поверхні циліндра дорівнює добутку довжини кола основи на висоту циліндра

S_б=2πRH

Повна поверхня циліндра складається з бічної поверхні та двох основ

S_повн=2πR(H+R)

П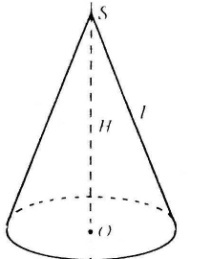 лоща бічної поверхні конуса дорівнює половині добутку довжини кола основи на його твірну

S_б=πRl

Повна поверхня конуса складається з бічної поверхні та основи

S_повн=πR(l+R)

Площа сфери

S=4πR²

4.4. Об’єм циліндра, конуса, кулі

Об’єм циліндра дорівнює добутку площі основи на висоту

V=πR²H

Об’єм конуса дорівнює третині добутку площі основи на висоту

V=1/3 πR²H

Об’єм кулі

V=4/3 πR³

Домашнє завдання Частина перша

1. Обчисліть площу бічної поверхні прямої призми, основа якої трикутник зі сторонами 20 см, 24 см і 26 см, а бічне ребро дорівнює 6 см.

2. Обчисліть площу бічної поверхні прямої призми, основою якої є паралелограм зі сторонами 10 см і 12 см, а бічне ребро дорівнює 10 см.

3. Обчисліть площу бічної поверхні прямої призми, основою якої є ромб зі стороною 8 см, а висота призми дорівнює 6 см.

4. Обчисліть об’єм призми, основою якої є паралелограм зі сторонами 16 см і 14 см та кутом 45 , а висота призми дорівнює см.

5. Сторона основи правильної трикутної призми дорівнює 14 см, а її бічне ребро см. Обчисліть об’єм призми.

6. Обчисліть об’єм правильної чотирикутної призми, сторона основи якої дорівнює 12 см, а висота – 14 см.

7. Обчисліть площу бічної поверхні правильної п’ятикутної піраміди, сторона основи якої дорівнює 6 см, а апофема – 10 см.

8. Обчисліть площу бічної поверхні правильної восьмикутної піраміди, сторона основи якої дорівнює 18 см, а апофема – 22 см.

9. Обчисліть об’єм піраміди, основою якої є прямокутник зі сторонами 26 см і 30 см, а висота піраміди дорівнює 25 см.

10. Обчисліть площу бічної поверхні правильної шестикутної піраміди, сторона основи якої дорівнює 4 см, а апофема – 5 см.

11. Обчисліть об’єм піраміди, основою якої є ромб з діагоналями 5 см і 9 см, а висота піраміди дорівнює 10 см.

12. Обчисліть об’єм піраміди, основою якої є паралелограм зі сторонами 8 см і 10 см та кутом 45 між ними, а висота піраміди дорівнює 18 см.

13. Обчисліть площу бічної поверхні циліндра, осьовим перерізом якого є квадрат зі стороною 8 см.

14. Чому дорівнює площа бічної поверхні циліндра, діаметр основи якого дорівнює 4 см, а твірна – 9 см?

15. Обчисліть площу бічної поверхні циліндра, висота якого дорівнює14 см, а радіус основи – 4 см.

16. Обчисліть об’єм циліндра, висота якого дорівнює 6 см, діаметр основи 4см.

17. Обчисліть об’єм циліндра, радіус основи якого дорівнює 7 см, а твірна 5 см.

18. Чому дорівнює висота циліндра, об’єм якого становить см³, а радіус основи дорівнює 2 см?

19. Обчисліть площу бічної поверхні конуса, твірна якого дорівнює 8 см, а радіус основи – 10 см.

20. Обчисліть площу бічної поверхні конуса, діаметр основи якого дорівнює 12 см, а твірна – 17 см.

21. Обчисліть площу бічної поверхні конуса, радіус основи якого дорівнює 3см, а твірна у 3 рази більша за радіус.

22. Обчисліть об’єм конуса, висота якого дорівнює 8 см, а радіус основи 9 см.

23. Радіуси основ циліндра і конуса рівні, висота циліндра дорівнює 8 см, а конуса – 6 см. Знайдіть відношення об’єму циліндра до об’єму конуса.

24. Обчисліть об’єм конуса, висота якого дорівнює 6 см, а радіус основи 5 см.

25. Висота конуса дорівнює 9 см, а його об’єм - 6π см³. Чому дорівнює площа основи конуса?

26. Чому дорівнює об’єм конуса, радіус основи якого , а висота дорівнює радіусу основи?

27. Чому дорівнює площа поверхні кулі, радіус якої дорівнює 6 см?

28. Чому дорівнює площа поверхні кулі, діаметр якої дорівнює 6см?

29. Знайдіть відношення площ поверхонь двох сфер, радіуси яких дорівнюють 5 см і 10 см.

30. Обчисліть об’єм кулі з радіусом 6 см.

31. Радіус однієї кулі у 2 рази більший за радіус другої кулі. Чому дорівнює об’єм кулі більшого радіуса, якщо об’єм кулі меншого радіуса дорівнює 1 см ?

32. Об'єм першої кулі у 27 разів більший за об’єм другої кулі. Чому дорівнює радіус першої кулі, якщо радіус другої кулі дорівнює 1 см?

33. Чому дорівнює радіус кулі, об’єм якої становить 36 см ?