Конус і площини

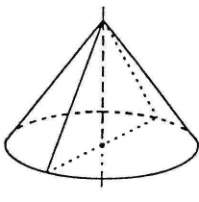
Осьовий переріз конуса утворюється площиною, яка містить вісь конуса; це рівнобедрений трикутник, бічні сторони якого – твірні конуса, а основа - діаметр основи конуса.

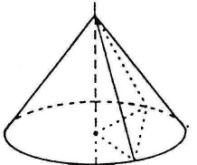
Переріз конуса площиною, яка проходить через його вершину, є рівнобедрений трикутник, у якого бічні сторони є твірними конуса.

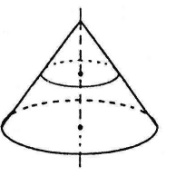
Площина, паралельна площині основи конуса, перетинає конус по кругу, а бічну поверхню – по колу з центром на осі конуса.

Зрізаний конус

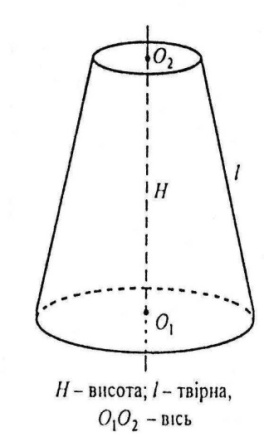
Зрізаний конус – це частина конуса, утворена перерізом конуса площиною, паралельною до основи, але не подібна до самого конуса.

Основи зрізаного конуса – два круга з різними радіусами.

Висота зрізаного конуса – це відстань між площинами його основ.

Вісь зрізаного конуса – це пряма, яка проходить через центри його основ.

Твірна зрізаного конуса – це частина твірного конуса, яка лежить між основами утвореного зрізаного конуса.

3.4 Куля та сфера. Взаємне розміщення площини та кулі. Площина, дотична до сфери

Куля – це тіло, що складається з усіх точок п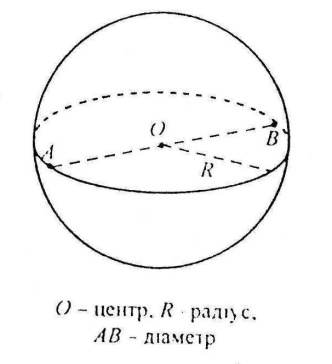 ростору, які знаходяться від даної точки (центра) на відстані, не більше за дану (радіус).

Сфера (кульова поверхня) – це межа кулі.

Діаметр – відрізок, який сполучає дві точки (діаметрально протилежні точки кулі) кульової поверхні і проходить через центр кулі.

Перерізи кулі

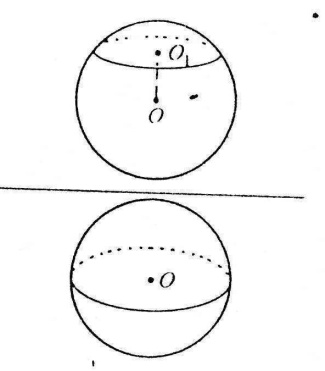
Будь-який переріз кулі площиною є круг; центр цього круга є основою перпендикуляра, опущеного з центра кулі на січну площину.

Площина, яка проходить через центр кулі, називається діаметральною площиною; вона утворює переріз кулі, який має назву великий круг.

Площина, що має одну спільну точку зі сферою, називається дотичною до сфери

Радіус, проведений в точку дотику, перпендикулярний до площини.

Домашнє завдання

1. У прямокутному паралелепіпеді AD = 24 см, CD = 5 см, = 10 см. Чому дорівнює площа прямокутника ?

2. Ребро куба дорівнює 2 см. Чому дорівнює площа трикутника ?

3. Діагональ основи куба дорівнює а. Чому дорівнює діагональ куба?

4. Основа прямої призми – трикутник зі стороною с і прилеглими до неї кутами і . Діагональ бічної грані, що проходить через сторону основи, яка протилежна куту , нахилена до площини основи під кутом . Знайдіть висоту призми.

5. Основа прямої призми — трикутник зі стороною , протилежним цій стороні кутом і прилеглим кутом . Діагональ бічної грані, яка містить стонону основи, до якої прилягають кути і , нахилена до площини основи під кутом . Знайдіть висоту призми.

6. Основа піраміди – трикутник зі сторонами 13 см, 14 см і 15 см. Знайдіть площу перерізу, який проходить паралельно площині основи і ділить висоту піраміди у відношенні 1:2, рахуючи від вершини піраміди.

7. Основа піраміди — трикутник зі стронами 6 см, 25 см і 29 см. Знайдіть площу перерізу, який проходить паралельно площині основи і ділить висоту піраміди у відношенні 1:3, рахуючи від вершини піраміди.

8. Висота циліндра дорівнює 6 см, а його об’єм – 18 см . Чому дорівнює площа основи циліндра?

9. Кут між твірною і площиною основи конуса дорівнює см. Знайдіть висоту конуса.

10. Кут між твірною і площиною основи конуса дорівнює 60 , висота конуса дорівнює см. Знайдіть твірну конуса.

11. Висота конуса дорівнює 14 см, а кут при вершині осьового перерізу – 120 . Знайдіть радіус основи конуса.

12. Радіус основи конуса дорівнює 12 см, а кут при вершині осьового перерізу – 120°. Знайдіть твірну конуса.

13. Паралельно осі циліндра, радіус основи якого дорівнює см, проведено площину, що перетинає основу циліндра по хорді, яка стягує дугу, градусна міра якої дорівнює 90°. Знайдіть площу перерізу, якщо кут між діагоналлю перерізу і вказаною хордою дорівнює 60°.

14. Висота циліндра дорівнює 8 см, радіус основи – 5 см. На відстані 4 см від осі циліндра паралельно їй проведено площину. Знайдіть площу перерізу, який при цьому утворився.

15. У нижній основі циліндра проведено хорду завдовжки 8 см, яка знаходиться на відстані 3 см від центра цієї основи. Знайдіть площу осьового перерізу циліндра, якщо його висота дорівнює 6 см.

16. Паралельно осі циліндра, радіус основи якого дорівнює 8 см, проведено площину, що перетинає основу циліндра по хорді, яка стягує дугу, градусна міра якої 120°. Знайдіть площу перерізу, якщо його діагональ дорівнює 16 см.

17. Через дві твірні конуса, кут між якими дорівнює , проведено переріз. Знайдіть площу цього перерізу, якщо висота конуса дорівнює h і утворює з його твірною кут .

18. Ч ерез дві твірні конуса, кут між якими дорівнює , проведено переріз. Знайдіть площу цього перерізу, якщо радіус основи конуса дорівнює , а твірна утворює з площиною основи кут .

19. У кулі з центром , зображеній на рисунку, проведено переріз з центром на відстані 12 см від центра кулі. Знайдіть радіус кулі, якщо радіус перерізу дорівнює 9 см.

19. У кулі проведено переріз на відстані 5 см від центра кулі. Знайдіть радіус перерізу, якщо радіус кулі дорівнює 13 см.