3 Геометричні тіла та поверхні

3.1 Поняття про геометричне тіло та його поверхню.

Многогранник і його елементи. Правильні многогранники.

Призми та їх види

Геометричне тіло – частина простору, обмежена якоюсь поверхнею.

М ногогранник – це таке тіло, поверхня якого складається із скінченної кількості плоских многокутників.

О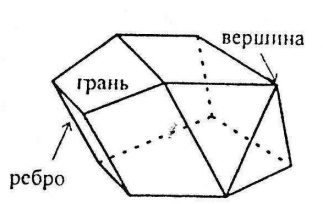 пуклим називається многогранник, який лежить по один бік від площини кожного з плоских многокутників (граней) на його поверхні; ребра – це сторони граней, вершини – вершини граней.

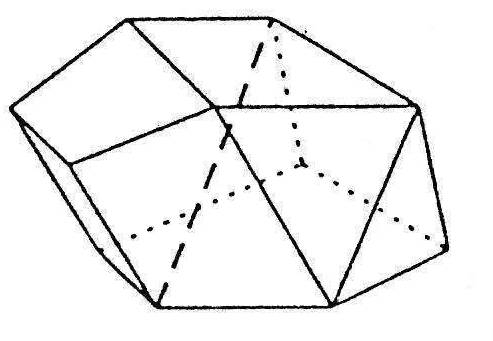
Діагоналлю многогранника називається такий відрізок, що сполучає дві вершини многогранника, який не лежить на грані многогранника і не є ребром.

Призма

Призма – це многогранник, який складається з двох плоских многокутників (основ), які лежать у різних площинах і суміщаються паралельним перенесенням, та всіх відрізків, що сполучають відповідні точки цих многокутників.

Висотою (Н) призми називається відстань між площинами її основ.

Властивості призми

Основи призми рівні.

Площини основ паралельні.

Усі бічні ребра рівні і паралельні.

Усі бічні грані – паралелограми.

П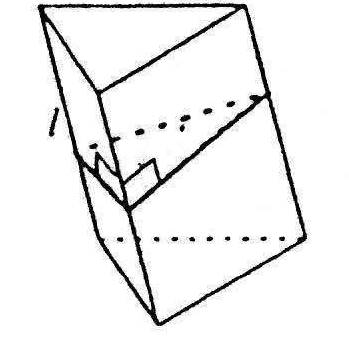 ерпендикулярний переріз призми

Перпендикулярним називається переріз призми площиною, перпендикулярною до бічного ребра призми, яка перетинає всі бічні ребра.

Пряма призма

Прямою називається призма, бічні ребра якої перпендикулярні до основ.

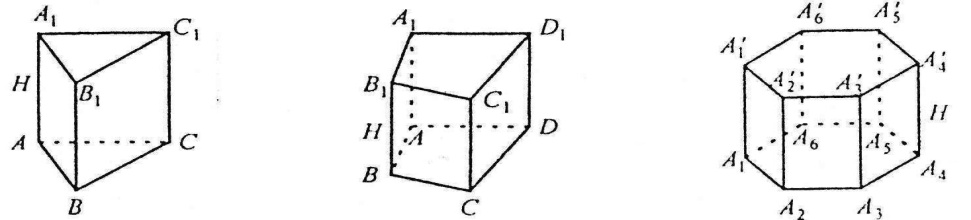
Правильною називається пряма призма, основи якої є правильними многокутниками.

Паралелепіпеди та їх види. Властивості діагоналей паралелепіпедів

Паралелепіпед – це призма, основи якої є паралелограми.

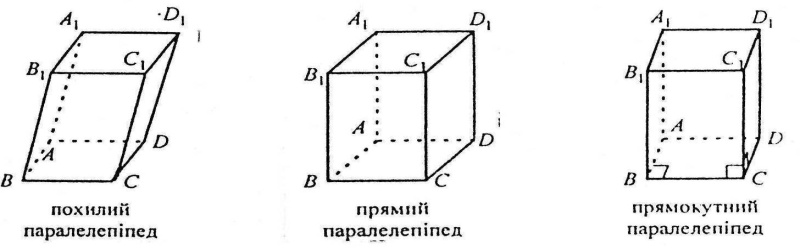
Грані паралелепіпеда без спільних вершин називаються протилежними.

Загальні властивості паралелепіпедів

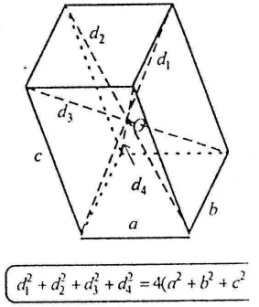
Кожна пара протилежних граней – рівні паралелограми, що лежать у паралельних площинах.

Діагоналі паралелепіпеда перетинаються в одній точці і точкою перетину діляться навпіл.

Точки перетину діагоналей є центром симетрії паралелепіпеда.

Сума квадратів діагоналей паралелепіпеда дорівнює сумі квадратів усіх його ребер.

Прямокутний паралелепіпед

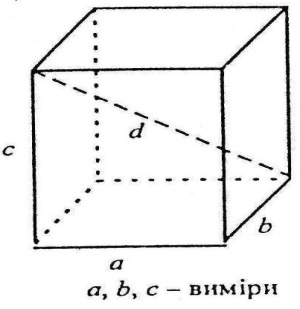
Прямокутним називається прямий паралелепіпед, основою якого є прямокутник.

Лінійними розмірами (вимірами) прямокутного паралелепіпеда називаються довжини ребер,що виходять з однієї вершини.

Усі грані прямокутного паралелепіпеда – прямокутники.

Квадрат кожної діагоналі дорівнює сумі квадратів лінійних розмірів:

d²=a²+b²+c²

К уб

Куб – це прямокутний паралелепіпед, у якого всі ребра рівні.

Усі грані куба – рівні квадрати.

3.2 Піраміди та їх види. Властивості паралельних перерізів у піраміді

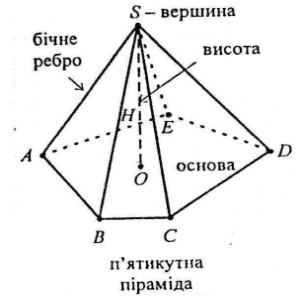
Піраміда – це многогранник, який складається з плоского многокутника (основи), точки (вершини), яка лежить у площині основи, і всіх відрізків, що сполучають вершину піраміди з точками основи.

В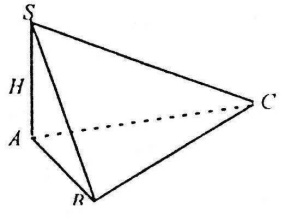 исотою піраміди називається перпендикуляр, опущений з вершини піраміди на площину основи.

Прямою називається піраміда, одне з бічних ребер якої перпендикулярне до основи (тобто збігається з висотою).

Тетраедр – інша назва трикутної піраміди.

Положення вершини піраміди

Вершина рівновіддалена від вершин основи тоді і тільки тоді, коли її проекція є центром описаного навкруги многокутника основи кола або усі бічні ребра однаково нахилені до площини основи.

Вершина рівновіддалена від сторін основи тоді і тільки тоді, коли її проекція є центром вписаного у многокутник основи кола або усі бічні грані однаково нахилені до площини основи.