5. О знака паралельності прямої і площини

Якщо пряма, яка не належить площині, паралельна якій-небудь прямій у цій площині, то вона паралельна і самій площині.

6. Я кщо через пряму, яка паралельна даній площині, проходить площина, що перетинає дану площину, то пряма, за якої перетинаються ці площини, буду паралельна даній прямій.

7. Д ві площини називаються паралельними, якщо вони не перетинаються.

8. Ознака паралельності площин

Я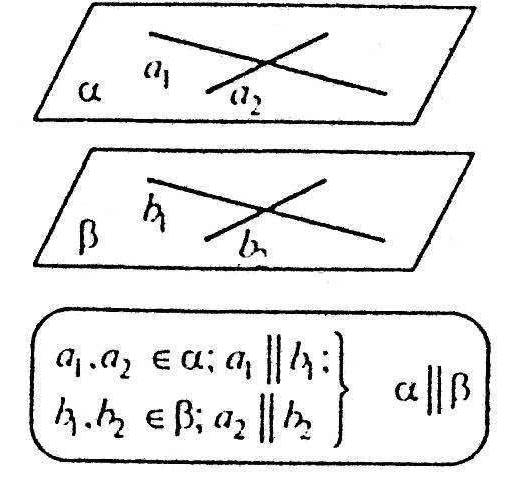 кщо дві прямі, які перетинаються, однієї площини відповідно паралельні двом прямим другої площини, то ці площини паралельні.

Властивості паралельних площин

9. Д 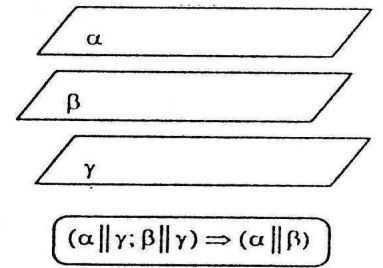ві різні площини, які паралельні третій, паралельні.

10. Через точку поза даною площиною можна провести площину, паралельну даній, і до того ж тільки одну.

11. Якщо дві паралельні площини перетинаються третьою, то прямі перетину паралельні.

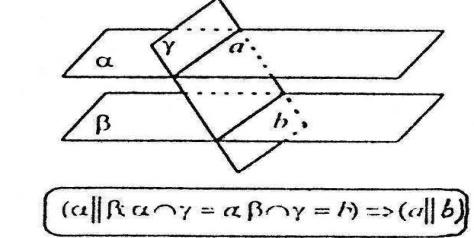
12. В ідрізки паралельних прямих, які містяться між двома паралельними площинами – рівні.

2.3 Зображення просторових фігур на площині

Д ля зображення просторових фігур на площині користуються паралельним проектуванням: такий спосіб відповідає зоровому сприйманню фігури під час їх розглядання здалеку.

Властивості зображення фігур на площині

П рямолінійні відрізки фігури зображуються на площині малюнка відрізками; паралельні відрізки фігури зображуються на площині малюнка паралельними відрізками.

С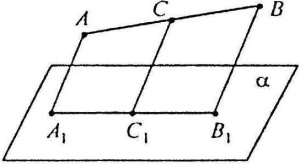 ередина відрізка при зображенні його на площині теж є серединою.

В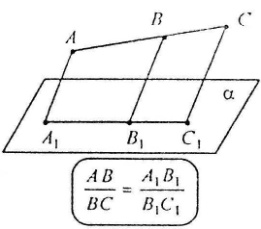 ідношення відрізків однієї прямої або паралельних прямих збігається при паралельному проектуванні.

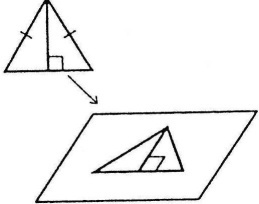
Проектування трикутників

При проектуванні будь-якого трикутника (гострого, тупокутного, прямокутного, рівнобедреного або рівностороннього) утворюється трикутник довільної форми (гострокутний чи тупокутний).

Проектування паралелограмів

Оскільки паралельність відрізків при проектуванні зберігається, паралелограми (а також прямокутники та квадрати) зображуються паралелограмами довільної форми.

При проектуванні ромба незмінною стає одна з діагоналей,

п роекцією є паралелограм.

Проектування трапеції

При проектуванні будь-яка трапеція (довільна, рівнобічна,

прямокутна) зображується як довільна трапеція.

Проектування кола

Коло при проектуванні на площину зображується як еліпс.

2.4 Перпендикулярність прямих і площин

Пряма, яка перетинає площину, називається перпендикулярною до цієї площини, якщо вона перпендикулярна до будь-якої прямої, що лежить у цій площині.

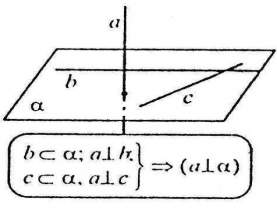
Ознака перпендикулярності прямої і площини

Якщо пряма перпендикулярна до двох прямих, які лежать у площині і перетинаються, то вона перпендикулярна до даної площини.

Властивості прямої і площини, перпендикулярних між собою

Я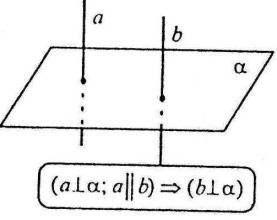 кщо площина перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна й до другої.

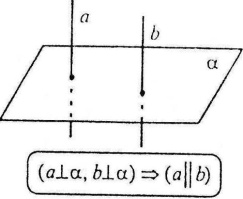
Дві прямі, перпендикулярні до однієї і тієї ж площини – паралельні.

П ряма, яка перпендикулярна одній із двох паралельних площин, перпендикулярна й до другої.

Я кщо пряма перпендикулярна до двох різних площин, то ці площини паралельні.