1 Координати і вектори у просторі
Вектори у просторі. Дії над векторами.
Розкладання вектора на складові
В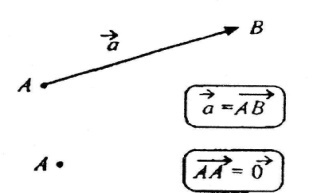
ідрізок,
для якого зазначено, який з його кінців
вважають початком,
а який – кінцем,
називається напрямленим відрізком, або
вектором.
Д
овжиною
(модулем) ненульового вектора
називається відстань між його початком
та кінцем.
Н
енульові
вектори називаються колінеарними,
якщо вони лежать або на одній прямій,
або на паралельних прямих.
Д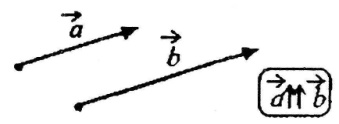
ва
однаково напрямлені колінеарних вектори
називаються співнапрямленими.
В
ектори
називаються рівними,
якщо
вони співнапрямлені і їх довжини рівні.
Сума двох векторів
П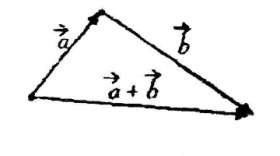
равило
трикутника. Сумою
двох векторів
називається вектор, відкладений від
початку першого вектора, кінець якого
збігається з кінцем другого вектора.
Закони додавання векторів
Переставний закон:
Сполучний закон:
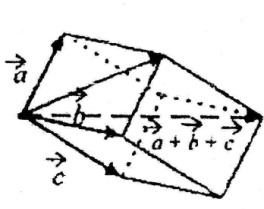
Правило паралелограма (на площині) Правило паралелепіпеда (у просторі)
Віднімання векторів
Р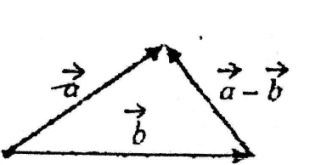
ізницею
двох векторів
називається такий вектор, сума якого з
другим вектором дорівнює першому.
П
ротилежним
даному називається вектор, протилежно
напрямлений з даним вектором, який має
ту саму довжину.
В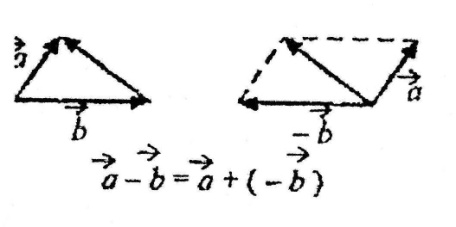
іднімання
двох векторів рівносильно додаванню
до першого вектора, протилежного другому.
Множення вектора на число
Множення вектора на додатне число
Д
обутком
ненульового вектора на число k
> 0
називається
такий вектор, співнапрямлений даному,
довжина якого дорівнює довжині даного
вектора, помноженій на
k.
Множення
вектора на нуль дає нульовий вектор:
Множення вектора на від’ємне число
Д
обутком
ненульового вектора на число k
< 0
називається
такий вектор, протилежно напрямлений
даному, довжина якого дорівнює довжині
даного вектора, помноженій на k.
Розкладання вектора за неколінеарними векторами
Н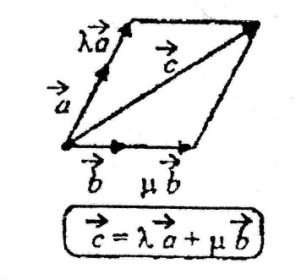
а
площині будь-який вектор можна розкласти
(записати у вигляді лінійної комбінації)
за двома не колінеарними векторами, при
цьому коефіцієнти розкладання визначені
однозначно.
У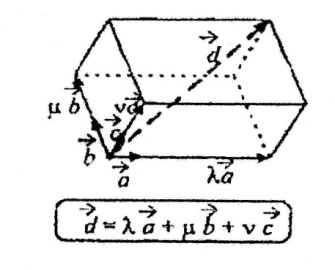
просторі будь-який вектор можна розкласти
за трьома векторами, що не лежать в одній
площині, при цьому коефіцієнти розкладання
визначені однозначно.
С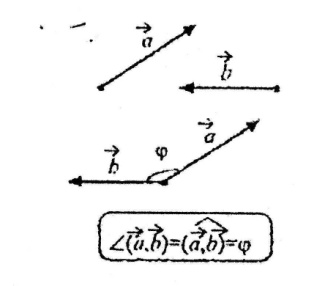
калярний
добуток векторів
Кутом між векторами називається кут, утворений рівними їм векторами, що відкладені від спільного початку.
Скалярним добутком двох векторів називаєтся добуток їх довжин на косинус кута між ними.
К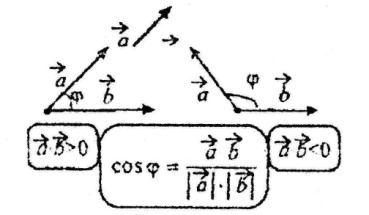
осинус
кута між векторами
дорівнює їх скалярному добутку, поділеному
на добуток довжин цих векторів.
Перпендикулярність векторів
Два вектори називаються перпендикулярними, якщо вони лежать на перепендикулярних прямих. Два вектори перпендикулярні тоді, і тільки тоді, коли скалярний добуток дорівнює нулю.
Скалярний квадрат вектора дорівнює квадрату його довжини.
1.2 Прямокутна система координат у просторі.
Дії над векторами, що задані координатами. Відстань між точками
Дії над векторами, заданими своїм координатами
Якщо початок вектора ā лежить у точці А(x1,y1,z1), а кінець – у точці В(x2,y2,z2), то координати вектора ā(x,y,z) знаходяться за формулою:
x=x2-x1 , y=y2-y1 , z=z2-z1
Нехай
дано вектори
ā
(x1,y1,z1)
і 
(x2,y2,z2)
ā+
=(
x1+x2,
y1+y2,
z1+z2)
ā - =( x1-x2, y1-y2, z1 –z2)
ā=
(
x1,
y1,
z1)
Ознака
колінеарності векторів:
ā ||
=
=
=
Скалярний
добуток
=
x1x2+y1y+z1z2
Довжина
(модуль) вектора ā
|ā|=
Косинус
кута між векторами cos
=
Якщо
x1x2+y1y2+z1z2 =0 - умова перпендикулярності векторів ā і .
Відстань між точками М1 (x1,y1,z1), М2(x2,y2,z2) обчислюється за формулою
|М1М2|= (x2-x1)2+(y2-y1)2+(z2-z1)2
Координати точки М(x,y,z), яка ділить відрізок М1М2 навпіл, обчислюються за формулами
x=
y=
z=